Книга: Наша математическая вселенная

Квантовая цензура

Квантовая цензура

Конец ноября 1991 года в Беркли. На улице темно. Я сижу за столом и отчаянно царапаю математические значки на обрывке бумаги. Я чувствую такой прилив возбуждения, какого прежде не бывало. Неужели я — маленький бестолковый я — только что открыл нечто по-настоящему важное?

Думаю, в науке нередко труднее всего даётся не поиск правильного ответа, а постановка правильного вопроса. Если вам попался действительно интересный, хорошо сформулированный физический вопрос, он может начать жить своей жизнью, сам подсказывая, какие вычисления нужно проделать, чтобы получить ответ, и всё остальное идёт почти механически. Даже если математические выкладки занимают часы и дни, это воспринимается в основном как рутинное вытягивание лески: надо же посмотреть на добычу. И я только что нашёл один из таких счастливых вопросов.

Я знал, что коллапс волновой функции можно элегантно описать посредством числовых таблиц, на квантово-физическом языке называемых матрицами плотности. В них закодировано не только состояние чего-либо (то есть волновая функция), но и, возможно, моё неполное знание этой волновой функции.[45] Так, если нечто может находиться лишь в двух местах, то моё знание этого можно описать таблицей чисел размером два на два:

В обоих случаях вероятность того, что я найду его в каждом из мест, составляет 0,5. Это кодируется двумя числами на диагонали обеих матриц (0,5 в левом верхнем углу и 0,5 в правом нижнем). Остальные два числа в каждой таблице (недиагональные элементы матрицы плотности) кодируют разницу между квантовой и классической неопределённостями. В случае, когда они тоже равны 0,5, мы имеем дело с квантовой суперпозицией (кот Шрёдингера либо жив, либо мёртв), но когда они равны нулю, фактически всё сводится к старой доброй классической неопределённости (как в случае, когда я забыл, где оставил ключи). Так что если вы сможете заменить недиагональные элементы нулями, то превратите «и» в «или» и вызовете коллапс волновой функции.

Копенгагенская интерпретация квантовой механики гласит: если ваш приятель наблюдает объект, не сообщая вам о результате, то он вызывает коллапс волновой функции, так что объект находится или здесь, или там, а вы просто не знаете, где. Иными словами, согласно копенгагенской интерпретации, наблюдатель некоторым образом обнуляет эти недиагональные члены. Я задумался: не может ли какой-нибудь менее загадочный физический процесс приводить к тому же эффекту? Если имеется изолированная система, которая не взаимодействует больше ни с чем, то, применяя уравнение Шрёдингера, легко доказать, что эти нежелательные числа никогда не исчезнут. Но реальные системы почти никогда не бывают изолированными, и меня заинтересовало, к чему это должно приводить. Например, когда вы читаете это предложение, с вами постоянно сталкиваются молекулы и фотоны. И если нечто находится в двух местах одновременно, что случится с таблицей чисел два на два, описывающей систему, которая испытывает воздействие внешних толчков?

Это был один из тех замечательных вопросов, которые сами дают на себя ответы, и всё остальное оказалось делом техники. Я рассмотрел объект и сталкивающуюся с ним частицу как единую изолированную систему и воспользовался уравнением Шрёдингера для вычисления того, что произойдёт. Спустя пару часов я сидел над листками с математическими символами, и у меня перехватывало дыхание: недиагональные члены стремились к нулю, как если бы волновая функция коллапсировала! Она, конечно, в действительности не коллапсировала, и соответствующие параллельные вселенные оставались в целости и сохранности, но это был совершенно новый эффект, который выглядел, как коллапс волновой функции, и запах имел, как коллапс волновой функции, и, как и при настоящем коллапсе, делал невозможным наблюдение объекта в двух местах одновременно. Так что квантовые причуды не прекращаются: они просто подвергаются цензуре!

Я пришёл к выводу, что квантовая механика требует секретности: объект может быть найден в двух местах сразу в состоянии квантовой суперпозиции лишь до тех пор, пока его положение остаётся в секрете для всего остального мира. Если секрет раскрывается, все эффекты квантовой суперпозиции становятся ненаблюдаемыми, и во всех практических отношениях он находится либо здесь, либо там, а вы просто не знаете, где. Если лаборант измеряет и записывает его положение, информация, очевидно, раскрывается. Но даже если один-единственный фотон отразится от объекта, информация об его местоположении также утечёт: она будет закодирована в последующем положении фотона. Спустя наносекунду (рис. 8.5) фотон будет находиться в двух разных местах в зависимости от положения объекта, так что, измерив этот фотон, вы узнаете, где зеркало.

Вернёмся к началу предыдущей главы: мы разбирались, нужен ли для коллапса волновой функции наблюдатель-человек — или достаточно робота. Теперь я убедился, что сознание никакой роли не играет, поскольку и одна-единственная частица может осуществить этот трюк: одиночный фотон, отразившись от объекта, вызовет тот же эффект, что и наблюдающий его человек. Я понял, что квантовое наблюдение связано не с сознанием, а просто с передачей информации. Вот почему мы никогда не видим макроскопические объекты в двух местах сразу, даже если они действительно находятся одновременно в двух местах: не потому, что они большие, а потому что их трудно изолировать! Шар для боулинга на свежем воздухе каждую секунду подвергается ударам 10²⁰ фотонов и 10²⁷ молекул воздуха. Я по определению не могу увидеть что-либо, не ударив по нему фотоном, поскольку видеть предмет можно только благодаря отражённым им фотонам (свету), так что шар для боулинга, находящийся в двух местах сразу, утратит своё состояние квантовой суперпозиции быстрее, чем у меня появится шанс обратить на него внимание. Напротив, если откачать молекулы воздуха хорошим вакуумным насосом, то электрон, как правило, сможет просуществовать около секунды без столкновений с чем-либо, и этого времени более чем достаточно, чтобы продемонстрировать странные свойства квантовой суперпозиции. Так, электрон затрачивает в квадриллион раз меньше времени (около 10^–15 секунды) на один оборот внутри атома, а значит, ничто не помешает ему находиться со всех сторон атома сразу.

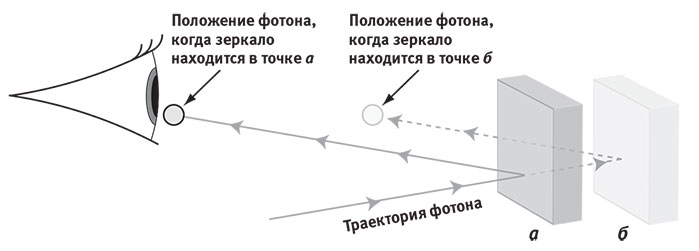
Рис. 8.5. Если фотографировать со вспышкой тёмную комнату, фотоны, возвращающиеся в камеру, будут нести информацию о том, что находится в комнате. Здесь показано, как даже одиночный фотон может «измерять» предметы: после того как он отразился от зеркала, информация о положении зеркала кодируется в его собственном положении. Если зеркало находится одновременно в положениях (а) и (б) в квантовой суперпозиции, то неважно, человек или фотон обнаружит, где оно: в любом случае квантовая суперпозиция разрушается.

Более того, если молекула воздуха отскочит от шара для боулинга и зафиксирует информацию об его положении в своём собственном положении (рис. 8.5), эта молекула вскоре столкнётся со многими другими молекулами, которые также получат эту информацию. Это похоже на публикацию секретных материалов на «Викиликс»: информацию копируют, затем копируют её копии, и вскоре кот высовывается из мешка настолько, что почти невозможно загнать его обратно. И так же, как вы не можете вновь засекретить распространившуюся информацию, нельзя восстановить квантовую суперпозицию. Теперь, наконец, понятно, почему параллельные вселенные III уровня остаются параллельными!

Я чувствовал, что той ночью ко мне пришёл успех. Вместе с тем я проработал вопрос в количественном аспекте. Большинство предметов могут находиться не в двух, а сразу во многих местах, и я рассмотрел этот случай (рис. 8.6). По сути, я открыл, что хотя фотон в основном разрушает квантовую суперпозицию, части её позволяет уцелеть: суперпозиция остаётся сравнимой по ширине с длиной волны фотона. Фотон, имеющий длину волны 0,0005 мм, действует практически так же, как наблюдатель, способный измерить положение предмета с точностью до 0,0005 мм. В предыдущей главе мы видели, что все частицы ведут себя, как волны, и характеризуются длиной волны. Я показал, что когда любая частица отскакивает от чего-либо, квантовая суперпозиция в масштабах, превосходящих длину её волны, разрушается.

Уже много лет я знал, что люблю физику и хочу посвятить ей жизнь. Я всегда задавался вопросом, смогу ли я сам что-нибудь привнести в неё, а не только изучать её, подбадривая с трибуны «игроков». Когда в ту ночь я отправился спать, то впервые в жизни подумал: «Да, я могу это!» Может быть, моё открытие назовут эффектом Тегмарка? Я знал: что бы ни случилось, я никогда не забуду тот вечер. Я чувствовал себя счастливым благодаря возможностям, которые у меня были, и замечательным людям, которые позволили мне присоединиться к великому делу развития науки. Мне казалось, что всё это слишком хорошо, чтобы быть правдой.

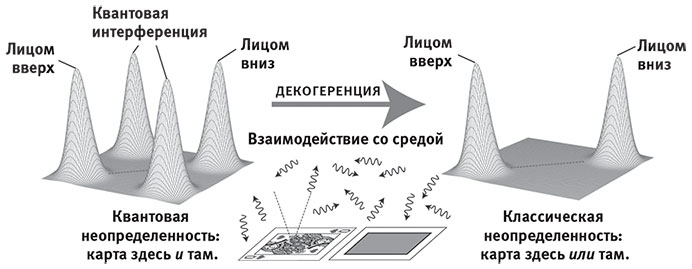
Рис. 8.6. Ваше знание о положении упавшей карты описывается матрицей плотности, которая может быть представлена в виде бугристой поверхности. Высота этой поверхности на диагонали (пунктирная линия) даёт вероятность того, что вы обнаружите карту в определённых местах, тогда как высота этой поверхности в других точках характеризует, грубо говоря, количество квантовых причуд, степень, в которой карта находится более чем в одном месте сразу. Левая матрица плотности соответствует карте, которая в равной мере находится в квантовой суперпозиции в обоих изображённых внизу положениях, на что указывают два пика, помеченных «Квантовая интерференция». После того, как от карты отразится фотон, декогеренция уничтожает эти два пика, приводя матрицу плотности к виду, изображённому справа. Она соответствует карте, фактически находящейся в одном из двух мест, но вы не знаете, в каком именно. Небольшая ширина этих пиков соответствует остающейся квантовой неопределённости вблизи положений лицом вверх и лицом вниз.

Так и оказалось. Через две недели я изложил свои соображения в первом черновике статьи, которую назвал «Кажущийся коллапс волновой функции, вызванный рассеянием». Рассеяние — это научный термин для описания поведения частиц, отскакивающих от вещества. Я впервые готовил статью для публикации и чувствовал себя, как ребёнок у рождественской ёлки. Я левша, и у меня ужасный почерк (почти каждое школьное задание возвращалось с пометкой «Поработайте над аккуратностью!»), так что было восхитительно видеть, как мои каракули превращаются в прекрасно набранные уравнения. В то же время было смешно, как я панически боялся, что найденное мной кто-то уже открыл. Я полагал, что нечто столь фундаментальное, если оно уже известно, должно упоминаться в учебниках и на моих аспирантских занятиях. Ничего подобного не было, но всё равно меня чуть не бросало в дрожь каждый раз, когда в процессе поиска литературы я открывал подозрительную ссылку. Пока всё было хорошо…

Готовясь к своей первой публикации, я даже изменил фамилию: вместо отцовской, Шапиро, взял материнскую — Тегмарк. В Швеции мне нравилось называться Шапиро. Мы привыкли быть единственной в стране семьёй с такой фамилией. А в международном научном сообществе Шапиро было столько, сколько в Швеции Андерсонов. Последней каплей стало то, что, введя в базе данных физических статей «М. Шапиро», я получил тысячи результатов. Даже на моём физическом факультете, в Беркли, нашлось трое М. Шапиро, и одна из них, Марджори, обучала меня физике элементарных частиц! Напротив, моя мать и её родственники были, насколько я могу судить, единственными Тегмарками на планете. Меня слегка тревожило, что отец может воспринять перемену фамилии как своего рода отстранение, но он заверил, что его это не беспокоит, процитировав Шекспира: «Что значит имя?»