Книга: Прикладные аспекты аварийных выбросов в атмосферу
4.2. Клубы
| <<< Назад 4.1. Струи |
Вперед >>> 4.3. Термики |
4.2. Клубы
Клубы являются одними из наиболее распространенных аварийных выбросов, возникающих при авариях взрывного характера. Клубом называется изолированный объем сплошной среды (газа или жидкости), сильно турбулизованной и имеющей характерные геометрические размеры (ширина, высота, длина) одного порядка. Из-за турбулентного характера движения среды внутри клуба его массовые, термодинамические и концентрационные характеристики могут считаться однородными по объему.
Для вывода уравнений, позволяющих получить газодинамические, геометрические и концентрационные характеристики клуба, движущегося в атмосфере, исходят из записи соотношений баланса массы, количества движения и энергии ограниченного объема в близкие моменты времени t1 и t2 [4, 33, 47, 73]. Уменьшая промежуток ?t = t2 — t1, приходят к дифференциальным уравнениям для усреднённых по объему выброса величин: концентрации i-ой примеси, плотности газа, скорости центра масс выброса, температуры его вещества, а также для геометрических величин: угла наклона вектора скорости центра масс выброса к горизонту и его объема.
Например, уравнение баланса массы клуба записывается так:
М2=М1+М?, (4.8)
где М = р· ? — масса клуба; М?= Е S? ?t — вовлекаемая в клуб масса воздуха; р, ? — плотность газа выброса и его объем; S? — боковая поверхность выброса (поверхность вовлечения); Е — вовлечение,
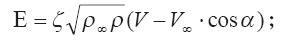
?, — коэффициент вовлечения, определяемый из эксперимента; V, V? — скорость клуба и скорость ветра; ? — угол наклона вектора скорости выброса к горизонту; индексы «1», «2», «?» относятся к моментам времени «1», «2», и к условиям окружающей среды соответственно.
Размерность Е — кг/(м2.с). Напомним, что овлечение — это масса газа окружающей выброс среды, вовлекаемая в него через единицу поверхности в единицу времени.
Из уравнения (4.8) следует, что масса выброса М2 в момент времени t2 складывается из массы выброса М1 в предыдущий момент времени t1, а также вовлеченной массы М.
В конечноразностном виде (5.8) имеет следующий вид:

Следует отметить, что клуб в сносящем ветровом потоке совершает сложное движение. Вовлекаемая в выброс масса окружающего воздуха передает ему количество движения, архимедова выталкивающая сила приводит к его всплытию.
Для плоского движения выброса уравнения силового баланса вдоль осей z их записываются так:

После раскрытия дифференциалов в левых частях этих уравнений приходим к соотношениям относительно параметров V и а. Они записываются так:
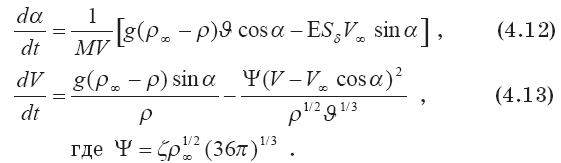
Уравнение сохранения концентрации химически активной примеси выводится по аналогии с уравнением сохранения массы. Баланс массы / — ой примеси выброса записывается так:
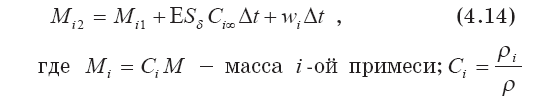
— массовая концентрация i— ой примеси; pi,wi — ее плотность и результирующая скорость образования i — го компонента в результате химических реакций;

Соотношение (4.14) после деления на ?t и устремления ?t ? 0 в дифференциальной форме принимает такой вид:
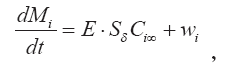
или, раскрывая дифференциал в левой части и воспользовавшись соотношением (4.9), получаем в окончательном виде уравнение для нахождения массовой концентрации i — ой примеси в химически реагирующем выбросе:
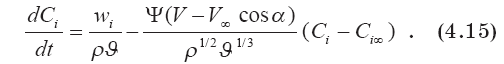
Энергия клуба изменяется за счет вовлечения воздуха окружающей среды, имеющего другую энергию, за счет изменения его высоты, а также за счет протекания химических реакций внутри его объема. Баланс энергии за интервал времени At записывается так:
(M?)2 (M?)1 + ES????t + wi qx ?t. (4.16)
В этом соотношении: Е и Н — полная энергия и полная энтальпия единицы массы газа;
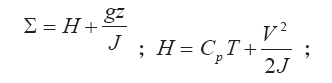
С?, Т — теплоемкость газа выброса при постоянном давлении и его температура; z — геометрическая высота выброса; g — ускорение силы тяжести; J — механический эквивалент тепловой энергии; qx — теплота химических реакций внутри выброса.
В результате вовлечения окружающего воздуха в клуб будет поступать энергия, содержащаяся в наружном воздухе, удельное значение которой записывается так:
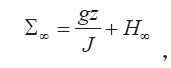
где
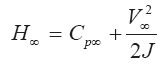
Соотношение (4.16) в дифференциальном виде запишется так:
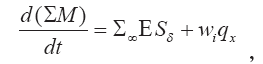
или после раскрывания дифференциала в левой части и использования соотношения (4.9)
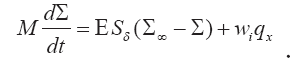
Подставив в (4.17) вместо ?, Е и S? их значения, можно получить соотношение для нахождения температуры вещества клуба. Оно имеет следующий вид:
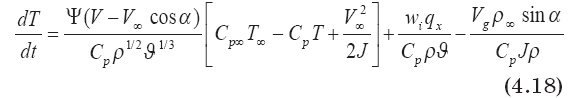
Дифференциальные уравнения (4.12), (4.13), (4.15), (4.18) дополняются соотношениями для нахождения молекулярного веса, теплоемкости и плотности газовой смеси выброса, а также уравнением состояния газа в виде
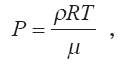
Необходимо отметить, что движение клуба в атмосфере является изобарическим. Это означает, что в любой момент времени и на каждой высоте его подъема давление газа внутри выброса в точности равно давлению окружающей среды на этой высоте, т. е. Р = Р?. (4.19)
При использовании (4.19) приходим к соотношению связи плотности вещества клуба с его температурой. Оно записывается так:
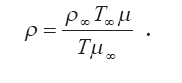
| <<< Назад 4.1. Струи |
Вперед >>> 4.3. Термики |
- Межклеточное вещество
- 04. На что влияет нагрев планет звездами, звезд Ядрами Галактик, Ядер Галактик Ядрами Сверхгалактик
- Список литературы
- Разные человечества
- Красные тучи, закрывающие солнце
- Московская белая
- Муравей, семья, колония
- Примерные рационы для котят от месяца до пяти и старше
- Голосеменные растения завоевывают мир
- Пароль скрещенных антенн
- Позор страны
- Что такое водопад?
