Книга: По кругу с Землей. Коперник. Гелиоцентризм.
ГИППОПЕДА
| <<< Назад ПЕРВЫЕ ГЕОЦЕНТРИЧЕСКИЕ ИДЕИ |
Вперед >>> ВИДИМОЕ ДВИЖЕНИЕ СОЛНЦА |
ГИППОПЕДА
Гиппопеда — это плоская кривая, которую можно получить сечением тора плоскостью, параллельной оси тора. Если большой радиус тора — R, а малый — r, то в декартовых координатах получившуюся фигуру можно описать так:
(x2+f)2 + 4r (r-R) (x2+y2) = 4 r2x2.
Это рациональная алгебраическая бициркулярная кривая четвертого порядка, симметричная относительно двух своих осей. Первым математиком, исследовавшим эти кривые, был Евдокс. На следующем рисунке приведены примеры гиппопеды.
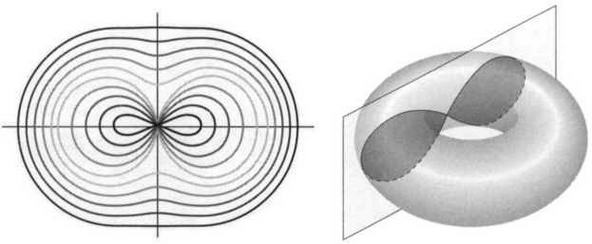
Слева — семейство гиппопед для случая 2 > R/r > 0,2. Справа — получение гиппопеды сечением тора плоскостью.
| <<< Назад ПЕРВЫЕ ГЕОЦЕНТРИЧЕСКИЕ ИДЕИ |
Вперед >>> ВИДИМОЕ ДВИЖЕНИЕ СОЛНЦА |
Оглавление статьи/книги
- УЧЕБА В БОЛОНЬЕ
- НОВАРА, ПРОФЕССОР БОЛОНЬИ
- ЛУННЫЙ ПАРАЛЛАКС
- ПЕРВЫЕ ГЕОЦЕНТРИЧЕСКИЕ ИДЕИ
- ГИППОПЕДА
- ВИДИМОЕ ДВИЖЕНИЕ СОЛНЦА
- ЮБИЛЕЙНЫЙ ГОД
- ВОЗВРАЩЕНИЕ В ПОЛЬШУ
- ИЗУЧЕНИЕ МЕДИЦИНЫ
- ПТОЛЕМЕЙ, БЛЕСТЯЩИЙ СИСТЕМАТИЗАТОР
- МЕДИЦИНА ВО ВРЕМЕНА КОПЕРНИКА
- «АЛЬМАГЕСТ»
- СЕМЕЙСТВО КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ИНТЕРЕС ДЛЯ АСТРОНОМИИ
- ПОПУЛЯРНОСТЬ ПТОЛЕМЕЯ
- ДИПЛОМ ПО РАСЧЕТУ
Похожие страницы
- НОВАРА, ПРОФЕССОР БОЛОНЬИ
- ВИДИМОЕ ДВИЖЕНИЕ СОЛНЦА
- ПТОЛЕМЕЙ, БЛЕСТЯЩИЙ СИСТЕМАТИЗАТОР
- ПЕРВЫЕ ГЕОЦЕНТРИЧЕСКИЕ ИДЕИ
- XVII. Сады в дикой глуши
- Электрогенераторы у рыб
- Для чего служат ракеты
- Сложный, «растущий» LECA и темные века эволюции эукариот
- Что мы знаем о мегамире?
- Морская торговля в Южной Америке и в Карибском море
- Рептилии защищаются
- Миф № 50 Если бы у обезьян родился мутант (прямоходящая обезьяна), они бы сразу убили его… Значит, эволюция невозможна!
