Книга: Астероидно-кометная опасность: вчера, сегодня, завтра
8.1. Явления, связанные с падением небесных тел
| <<< Назад Глава 8 Последствия падений крупных небесных тел на землю |
Вперед >>> 8.2. Последствия ударов о поверхность |
8.1. Явления, связанные с падением небесных тел
Часто увидишь, как звезды — лишь ветер задул с небосклона, вдруг упадают стремглав, и как сквозь суморок ночи пламя у них за спиной, белея, тянется длинно.
8.1.1. Взаимодействие небесных тел с земной атмосферой. Торможение метеороида в воздухе. Космическое тело, если оно движется сквозь атмосферу без разрушения и существенной абляции (потери массы), тормозится, когда его масса сравнивается с массой воздуха в цилиндре, имеющем такую же площадь поперечного сечения, что и само тело. Поэтому критерий отсутствия торможения неразрушающегося тела на высоте h можно записать в следующем виде:
?аH (sin ?)-1? 2 ?bRb,
где H — характеристическая высота атмосферы (H = 8,5 км), ? — угол наклона траектории тела к горизонту, ?b и Rb — плотность и радиус тела соответственно, а ?а — плотность атмосферы на высоте h.
Можно определить размер неразрушающегося тела, которое долетит до Земли без торможения, из условия
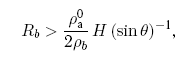
где ?0 а — плотность воздуха у поверхности Земли (h = 0, ?0а = 10-3 г/см3).
Для вертикального падения (? = 90°) ледяного тела (?b = 1 г/см3) получаем Rb > 4 м.
Таким образом, если бы тела не разрушались, то относительно небольшие метеороиды достигали бы поверхности Земли со скоростью, близкой к начальной. Но космические тела разрушаются в полете под действием аэродинамических сил: они могут распадаться на фрагменты, изменять свою форму и площадь поперечного сечения [Мелош, 1994; Melosh, 1981; Passey and Melosh, 1980].
Анализ наземных и спутниковых наблюдений за входом в атмосферу метеороидов с характерными размерами порядка 1–3 м показывает, что они разрушаются на высотах 25–45 км, не достигая Земли [Chyba et al., 1993; Svetsov et al., 1995; Nemtchinov et al., 1997a]. С увеличением размера тела его прочность снижается, так как в большом теле больше дефектов, а также трещин, возникновение которых связано с предыдущими столкновениями в космическом пространстве. К тому же, для того чтобы разделить тело на части, необходима энергия, пропорциональная его площади, в то время как запасенная в теле упругая энергия, связанная с аэродинамической нагрузкой, пропорциональна объему. Поэтому можно ожидать, что более крупные тела (> 10 м) начинают разрушаться на еще больших высотах. Следует также отметить, что абляция, вызванная теплопроводностью и переносом излучения в ударно-сжатом воздухе, незначительна для тел c размерами больше 10 м [Немчинов, Цикулин,1963; Немчинов и др., 1976; Baldwin and Sheafler, 1971; Biberman et al., 1980].
Деформация тела, вызванная аэродинамическими силами. Сильно фрагментированный объект может быть легко деформирован и становится подобным жидкости [Григорян, 1979]. При аналитических оценках используется предположение, что под действием аэродинамических сил во время полета оно расплющивается — увеличивается отношение его диаметра к высоте [Melosh, 1981; Ivanov et al., 1986; Chyba et al., 1993] — тело превращается в «блин» (pan-cake). Степень расплющивания может быть оценена из простых соображений. Давление на лобовой поверхности тела максимально в его критической точке и уменьшается к боковым поверхностям. Наличие градиента давления вызывает движение жидких частиц (или квазижидких частиц разрушенного материала) вдоль лобовой поверхности в радиальном направлении. Скорость этого поперечного движения Vt может быть оценена из следующего выражения [Григорян, 1979; Hills and Goda, 1993]:
Vt = (?а/?b)1/2V,
где V — скорость тела, ?b — его плотность, ?а — плотность атмосферы. Если плотность атмосферы убывает с высотой по экспоненциальному закону, то легко получить выражение, определяющее критический радиус R*b, когда тело расширяется до радиуса, примерно равного его начальному диаметру:
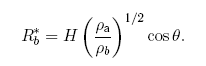
Если Rb < R*b, то может произойти деформация тела или его разрыв на отдельные части с последующим рассеянием частей фрагментированного тела. Критический диаметр для метеороидов в атмосфере Земли составляет 580, 330 и 200 м для ледяного, каменного и железного тел соответственно [Мелош, 1994].
Фрагментация и разрушение метеороида в атмосфере. Большие метеороиды (> 1 км) ударяются о поверхность Земли, почти не успев изменить форму и массу после прохождения через атмосферу. Судьба мелких тел зависит от их характеристик — состава, скорости, прочности, формы. Атмосфера оказывает большое влияние на последствия их ударов. Отсутствие кратера после падения Тунгусского космического тела диаметром 50–100 м показывает, что атмосфера может предотвратить образование кратера и ослабить сейсмические эффекты. Но железные тела того же размера достигают поверхности Земли. Так, известный 1-километровый кратер в Аризоне, возникший 50 000 лет назад, был образован падением железного тела диаметром 30–40 м [Мелош, 1994; Melosh and Collins, 2005]. На Земле было найдено довольно много кратеров меньших размеров, например 100-метровый кратер Kaaли в Эстонии возрастом приблизительно 4000 лет [Пиррус, Тиурма, 1987]. Еще несколько подобных кратеров в Эстонии возрастом в несколько тысяч лет имеют диаметры 40, 30 м и менее. Сихотэ-Алинский железный метеоритный дождь 1947 г. создал массу мелких кратеров (диаметр наибольшего из них около 26,5 м) и огромное число мелких фрагментов [Кринов, 1981; Кринов, Фонтон, 1959; Немчинов, Попова, 1997]. Начальная кинетическая энергия этого метеороида по оценкам составила около 10 кт тринитротолуола (ТНТ), масса — около 200 т. Поверхности достигли крупные фрагменты с энергией, соответствующей примерно 100 т ТНТ. Остальная энергия перешла в энергию нагретого воздуха и продуктов абляции. Хотя железные тела составляют только 6–7 % от всех падающих на Землю тел [Shoemaker, 1983], они легче проходят сквозь атмосферу и чаще встречаются в качестве находок.
Численное моделирование деформации и фрагментации метеороида. Действие аэродинамических сил — основная причина деформации и разрушения тел, попадающих в атмосферу. Применение модели «блина» ограничивается некоторой величиной fp отношения радиуса «блина» R к начальному радиусу тела Rb. Величина фактора расширения fp в разных работах принимается равной 2–7 в зависимости от некоторых дополнительных соображений, иногда не вполне корректных. Влияние этого фактора на параметры разрушенного тела (т. е. роя фрагментов и пара) на поздней стадии торможения, очевидно, очень велико, так как он определяет диаметр поперечного сечения, а с ним и скорость тела (струи), и температуру воздуха в ударной волне, и т. д. Таким образом, простые модели могут дать весьма грубые результаты. Более точные предсказания должны основываться на более сложном прямом численном моделировании падения.
Прямые численные расчеты двумерной гидродинамической задачи падения тела в атмосфере были выполнены, например, в работе [Hazins and Svetsov, 1993] с использованием лагранжева метода и в работе [Teterev et al., 1993] эйлеровым методом со специальным способом маркировки границы тела. Ледяное космическое тело, движущееся сквозь атмосферу, рассматривалось как жидкость с уравнением состояния воды. Расчеты показали, что метеороид в определенных ситуациях расплющивается незначительно. Он постепенно теряет свою массу вследствие сдува вещества поверхности воздухом. Под действием неустойчивостей раздробленное тело может принимать различную форму, которую заранее невозможно точно предсказать. В некоторых случаях тело стремится принять коническую форму и легче выдерживает полет сквозь атмосферу. В других случаях оно раздувается и принимает форму тора. При скорости входа в атмосферу 20 км/с 200-метровое ледяное тело теряет перед падением на поверхность менее 20 % своей начальной кинетической энергии, но увеличивает свой радиус приблизительно до 300 м на высоте 6,5 км над поверхностью Земли. На еще более низких высотах тело разрушается на мелкие фрагменты, которые на момент падения рассеиваются на расстояния вплоть до 200 м от центра падения метеороида. Масса этих фрагментов составляет 80 % от начальной массы, и их энергия достигает более чем 70 % от начальной энергии метеороида. Несмотря на разрушение тела, единая ударная волна охватывает все фрагменты. Подобные численные расчеты были проведены и для большего тела с диаметром 400 м. В этом случае тело деформируется, и при достижении поверхности Земли его полная масса уменьшается лишь на 10 %.
В работе [Teterev and Nemtchinov, 1993] была развита численная модель «мешка с песком», в которой считалось, что метеороид представляет собой совокупность частиц, движущихся сквозь атмосферу. Частицы передают энергию и импульс атмосфере и охватываются единой огибающей их ударной волной. С помощью этого метода также было показано, что сильно фрагментированный метеороид принимает коническую форму (рис. 8.1) и теряет меньше энергии, чем это было предсказано с помощью простых полуаналитических моделей дезинтеграции.
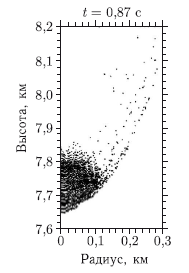
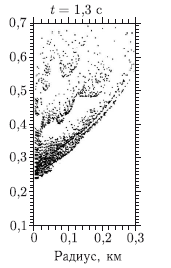
Рис. 8.1. Положения характерных частиц в модели «мешка с песком» для двух моментов полета t. Предполагается, что метеороид был мгновенно фрагментирован на высоте 25 км на 106 каменных фрагментов, заполняющих сферу с диаметром 200 м, и имел скорость 20 км/с
В расчетах предполагалось, что каменный метеороид после начальной стадии фрагментации состоит из 106 каменных фрагментов, свободно упакованных в сфере диаметром 200 м, скорость их составляет величину 20 км/c. В расчетах использовались пять групп фрагментов с радиусами от 10 см до 10 м, средний радиус составлял 1 м. Перед падением диаметр сферы, содержащей основную часть каменных фрагментов, увеличивался приблизительно до 400 м. Вследствие увеличения объема тела перед падением и уменьшения его средней плотности механический импульс, передаваемый поверхности Земли, будет меньше, чем для более компактного тела, и большая часть кинетической энергии тела будет превращаться в энергию поднимающегося факела.
След за телом. Космическое тело, проходящее сквозь атмосферу, создает за собой нагретый след, который расширяется до тех пор, пока давление в нем не сравняется с атмосферным. При расширении плотность в следе понижается. Воспользуемся очень простой идеализированной моделью цилиндрического сильного взрыва: тонкий ударно-сжатый слой с выровненным давлением внутри этой оболочки. Будем считать, что разреженная полость за фронтом расширяется до момента времени, когда давление на фронте становится примерно равным атмосферному давлению pа. Отсюда получаем, что радиус следа Rw определяется соотношением
Rw ? Rb(p0/pа)1/2, или Rw ? Rb(V/Ca) ??,
где p0 — давление на лобовой поверхности затупленного тела (p0 ? ?аV 2, ?a — плотность воздуха, ? — показатель адиабаты), Cа — скорость звука в холодном воздухе. При V = 15 км/с, Cа = 0,3 км/с получаем Rw/Rb ? 60. Таким образом, для тела диаметром 0,2 км диаметр следа будет достигать Rw ? 12 км. В действительности, за время пролета тела сквозь слой толщиной порядка характеристической высоты атмосферы H след не успевает расшириться до своего предельного размера.
След является разреженным каналом, через который некоторая часть энергии и массы может покидать плотные слои атмосферы, на его размер влияет и разрушение тела. Поэтому более полную картину можно получить только путем численного расчета.
На рис. 8.2 приведены результаты расчета по программе SOVA [Shuvalov, 1999] пролета ледяного тела (?b = 1 г/см3) сквозь атмосферу при начальном диаметре 200 м и начальной скорости 50 км/с, т. е. при массе 4 106 т и начальной энергии, эквивалентной 300 Мт ТНТ. Видно, что к моменту времени, когда струя фрагментов подлетела к Земле, диаметр струи превышал 1 км. Через 1 с после удара характерный поперечный диаметр горячей области и области повышенного давления составил уже около 10 км.
При меньших начальных размерах тела струя фрагментов и воздуха вообще не достигает Земли. Именно это имело место в случае Тунгусского падения в 1908 г., когда метеороид имел размер не более 100 м. Наоборот, при падении крупного тела практически вся масса тела почти без торможения и абляционных потерь достигает поверхности Земли.
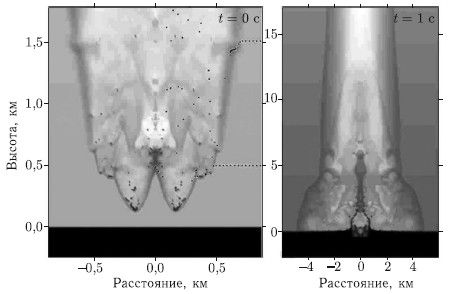
Рис. 8.2. Распределение плотности при пролете сквозь атмосферу ледяного тела с начальными диаметром 200 м и скоростью 50 км/с
8.1.2. Ударная волна. Оценка параметров ударной волны. После удара космического тела о поверхность Земли его кинетическая энергия превращается в тепловую и кинетическую энергии вещества грунта за фронтом ударной волны, распространяющейся в грунте от точки удара, и в энергию парового факела, выбрасываемого в атмосферу. Этот факел взаимодействует с атмосферой Земли и выделяет часть своей энергии в воздухе, также генерируя в нем ударную волну [Мелош, 1994; Ahrens and O’Keefe, 1987; O’Keefe and Ahrens, 1982a; Roddy et al., 1987].
Если ударяющее тело имеет низкую плотность по сравнению с плотностью грунта, а влиянием следа и неоднородности атмосферы можно пренебречь, то простейшую оценку параметров ударной волны в воздухе можно сделать, предположив, что вся энергия тела превращается вблизи точки удара в энергию полусферической волны. В свою очередь, для определения параметров ударной волны такого взрыва можно использовать или эмпирические данные, например представленные в виде аналитической формулы Садовского [Садовский, 2004], или результаты одномерных численных расчетов [Brode, 1955; Охоцимский и др., 1957]. Естественно, необходимо учитывать, что при прохождении космическим телом атмосферы часть его энергии выделяется в воздухе и энергия «приземного» взрыва, соответственно, меньше начальной.
Проблема определения опасностей, связанных с ударами астероидов и комет, является многофакторной, так как результат зависит от начальной скорости, массы, плотности, состава, формы, структуры и прочности тела, угла наклона его траектории, плотности и состава грунта в месте удара и т. д. Численные расчеты двумерных, а тем более трехмерных физико-математических задач о прохождении разрушающегося тела сквозь атмосферу и ударе о Землю являются весьма трудоемкими. Поэтому естественными являются попытки построения приближенных моделей для оценки результатов удара. Одной из таких моделей, доведенных до удобной в использовании программы, является программа, созданная в Аризонском университете (модель СММ) [Collins et al., 2005] и размещенная на сайте этого университета (www.lpl.arizona.edu/ImpactEffects). В силу желания получить простой и удобный в использовании инструмент для оценок авторы прибегли к ряду упрощений, которые подчас применимы не ко всем ситуациям, возникающим при ударах. При расчете параметров ударной волны были использованы данные, полученные при наземных и приземных ядерных взрывах [Glasstone and Dolan, 1977], и принцип энергетического подобия. В действительности область энерговыделения при входе метеороида является не точечным и не линейным источником, что видно из результатов расчета даже вертикального удара (рис. 8.2). И тем более сложной является картина взаимодействия ударной волны с поверхностью при косом ударе. Расчет прохождения тела сквозь атмосферу в программе СММ для рассматриваемых здесь достаточно больших тел (размером в десятки, сотни и более метров) проводится по модели растекающегося «блина» [Chyba et al., 1993] с фактором расширения fp = 7. Считается, что при достижении этого расширения оставшаяся энергия выделяется в воздухе. Если же эта степень расширения не достигается вплоть до поверхности Земли, то предполагается, что остатки ударяют о поверхность, приводя к образованию кратера, выбросу вещества, сейсмическому эффекту и формированию ударной волны в воздухе.
Приведем результаты расчетов по программе СММ для вертикального удара кометы (плотностью 1 г/см3) диаметром 200 м при начальной скорости 50 км/с и каменного тела (плотностью 2,7 г/см3) диаметром 400 м при начальной скорости 17 км/с. В обоих случаях будем считать грунт плотным, скалистым. В первом случае (в дальнейшем — вариант 1) начальная кинетическая энергия равна 1,2 103 Мт ТНТ. По модели СММ фрагменты тела ударяют по поверхности со скоростью 32 км/с в пределах круга диаметром 0,7 км, энергия ударяющих о поверхность струи пара и фрагментов составляет около 500 Мт ТНТ. На расстоянии 15 км амплитуда ударной волны, по оценке СММ, составляет 1,8 бар. При таком давлении, согласно работе [Glasstone and Dolan, 1977], многоэтажное кирпичное здание с несущими стенами обрушится. Во втором случае (в дальнейшем — вариант 2) начальная кинетическая энергия несколько больше, чем в варианте 1, а именно 3,1 103 Мт ТНТ. Эллипс рассеяния по оценке СММ составляет 0,58 ? 0,58 км, амплитуда ударной волны при скорости 16,7 км/с на расстоянии 20 км равна 3,2 бар, что также приводит к обрушению многоэтажного кирпичного здания. Будет повреждено и многоэтажное здание со стальным каркасом. В двух вариантах, выбранных нами для примера (комета и каменное тело), скорости входа соответствуют типичным скоростям входа таких тел. Размеры выбраны сравнительно небольшими. Они соответствуют, по нашему мнению, нижней границе размеров объектов, которые следует считать опасными. Они вызывают последствия, которые можно рассматривать в некоторых случаях как локальные катастрофы (ударная волна и пожары, кратеры и навал), в других — как региональные (цунами), а в третьих — возможно, как глобальные (ионосферные и магнитосферные возмущения, см. ниже). При увеличении диаметра тела и его энергии возрастает роль следа и неоднородности атмосферы в распространении ударной волны, и использование данных ядерных испытаний и энергетического подобия становится невозможным.
Характеристический размер ударной волны воздушного взрыва зависит от его энергии и пропорционален радиусу тела. Для тела размером Rb = 100 м и скоростью 50 км/с размер ударной волны может достигать 8 км, что близко к величине характеристической высоты атмосферы H. Для таких сравнительно небольших тел существенную роль играет след, и взрывная волна по форме сильно отличается от сферической. Неоднородность атмосферы также приводит к сильному отличию формы ударной волны от сферической.
Как видно из рис. 8.2, для кометы с Rb = 100 м диаметр области повышенного давления на поверхности Земли составляет примерно 10 км. Средняя скорость распространения ударной волны по поверхности при этом составляет примерно 5 км/с, т. е. волна еще сильная. Однако максимальное давление в ней намного меньше, чем в случае, если бы тело достигло Земли не разрушившись. Поэтому и размер кратера, и сейсмическая эффективность, и эффективность возникновения цунами (при ударе о воду) также намного меньше, чем для более крупных тел. В то же время эффективность воздействия ударной волны на сооружения, расположенные на поверхности, не слишком снижается по сравнению с таковой для воздушного взрыва с той же энергией. Систематические расчеты параметров ударных волн и механического действия на грунт или воду при различных размерах астероидных или кометных тел (в диапазоне 100–1000 м), различных начальных скоростях и углах наклона траектории еще предстоит произвести. Это позволит уточнить сейсмическую и цунамигенную опасность таких тел.
Избыточное и динамическое давления. Эффекты разрушения, вызванные взрывной волной, обычно соотносят с максимумом избыточного давления. В Нагасаки жилые дома разрушились на расстоянии вплоть до 2 км от эпицентра взрыва, где максимум избыточного давления ?p по оценкам составлял 20 кПа [Glasstone and Dolan, 1977]. Результаты ядерных испытаний показывают, что почти полное разрушение двухэтажного деревянного каркасного дома и неукрепленного кирпичного дома происходит при ?p = 30–35 кПа, прочный дом с каркасом из стали с алюминиевыми панелями обваливался при ?p = 20 кПа. Максимум избыточного давления, вызванного ударной волной, зависит не только от расстояния до эпицентра, но также от высоты взрыва. Величина ?p = 30 кПа достигалась на расстоянии 5 км от эпицентра для ядерного взрыва с энергией 1 Мт, когда он происходил на поверхности, и на расстоянии 9 км при взрыве на высоте 3,6 км [Glasstone and Dolan, 1977]. Для взрыва с энергией 30 Мт простые оценки, основанные на гидродинамическом подобии, дают радиус поражения R = 25 км при взрыве на высоте 10 км. Таким образом, размеры областей, которые могли бы быть опустошены падением метеороида с энергией около 30 Мт, сравнимы с радиусом крупного города. Существует другой важный фактор — динамическое давление, которое определяет повреждения, вызванные сильными ветрами, возникающими за фронтом взрывной волны. Для ?p = 35 кПа максимальное динамическое давление q = 4 кПа и максимальная скорость ветра составляет 260 км/ч. Но мы не будем углубляться в такие детали. Лишь упомянем, что полученная с помощью теоретических газодинамических расчетов [Коробейников и др., 1991] зона разрушения лесного массива неплохо согласуется с данными натурных исследований зоны воздействия при Тунгусском событии 1908 г.
Оценки величины зоны разрушений ударными волнами, вызванными падениями астероидов и комет, были даны в работе [Chapman and Morrison, 1994]. Авторы принимали во внимание избыточное давление на фронте ударной волны и динамическое давление, которое вызвало падение деревьев. Для калибровки они использовали Тунгусское событие [Зоткин, Цикулин, 1966], где ударные волны вызвали падение деревьев на площади 2000 км2, которая эквивалентна площади круга с радиусом Rs = 25 км. Предполагалось, что площадь As сильных повреждений строений приблизительно равна площади вывала леса. Для оценок может быть использовано следующее выражение:
As = ?R2 s = 200E2/3 k, Rs = 8Ek1/3,
где радиус Rs выражен в километрах, площадь As — в квадратных километрах, энергия ударяющего тела Ek — в мегатоннах. Коэффициенты в формуле изменяются с высотой взрыва. «Оптимальная» высота h [км] составляет 6,4E1/3 [Glasstone and Dolan, 1977; Hills and Goda, 1993]. Если высота взрыва уменьшается до нуля, радиус Rs уменьшается приблизительно в 1,4 раза. Для E = 30 Мт получается радиус Rs = 18 км.
Прорыв атмосферы. Законы подобия, которыми мы пользовались для оценок, основаны на теоретических исследованиях гидродинамической задачи о распространении ударной волны после точечного взрыва в однородной атмосфере и на исследованиях с помощью численного эксперимента распространения взрывных волн, образованных химическими взрывами с высокой энергией и ядерными взрывами с энергиями менее 10 Мт. Но для больших энергий радиус Rs оказывается порядка характерной высоты атмосферы или превышает ее (для E = 103 Мт мы получаем Rs = 80 км), поэтому оценки следует уточнять численными расчетами.
Двумерные численные расчеты взрыва в неоднородной атмосфере и различные теоретические оценки прорыва атмосферы показывают, что ударная волна вследствие уменьшения плотности воздуха с высотой над поверхностью Земли движется вверх быстрее, чем в радиальном направлении. Численные расчеты [Jones and Sanford, 1977; Jones and Kodis, 1982] взрыва с энергией 500 Мт, произведенного на поверхности, показали, что динамическое давление превосходит порог вывала леса на расстояниях в 27,5 км вместо 45 км, как это следует из закона подобия. В действительности давление и скоростной напор снижаются еще больше за счет влияния следа, не учтенного в этих расчетах.
Результаты расчета для большого тела (диаметром 10 км) приведены на рис. 8.3. Картина распределения плотности и температуры в более поздние моменты времени показана на рис. 8.4. Хотя след здесь также присутствует, но выброс вверх в основном облегчен за счет быстрого падения плотности атмосферы с высотой.
8.1.3. Световой импульс и пожары. Падение Тунгусского космического тела 30 июня 1908 г. вызвало пожар на площади около 500 км2 [Vasilyev, 1998], что в 4 раза меньше, чем площадь опустошения леса взрывными волнами (2000 км2). Этот пожар наглядно демонстрирует роль светового излучения. В Хиросиме и Нагасаки 20–30 % всех жертв были ранены за счет ожога от прямого действия теплового излучения вспышки. Используя эти данные, можно ожидать, что лучистое воздействие при энергии взрыва в 10–30 Мт могло бы быть причиной ожогов незащищенной кожи первой степени (обратимое повреждение) для 82 % населения, а 15 % получили бы ожоги второй степени (которые можно вылечить за одну или две недели) [Glasstone and Dolan, 1977]. Конечно, жертвы прямого действия теплового излучения вне зоны «огненного шара» могут быть сокращены простыми способами гражданской обороны (убежище и другие меры защиты) при условии предупреждения о возможном падении космического объекта. Мы должны упомянуть также глазные травмы, вызывающие слепоту и ожоги сетчатки, но они также могут быть сокращены адекватной тренировкой использования специальных фильтров для глаз, опять же при условии предупреждения об опасности.
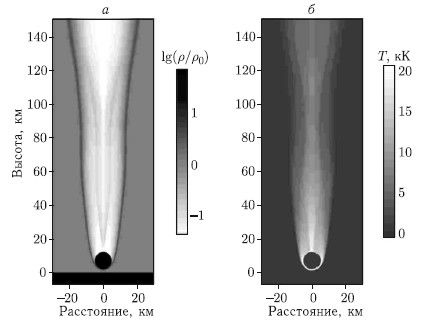
Рис. 8.3. Распределение относительной плотности (а) и температуры (б) непосредственно перед столкновением каменного тела диаметром 10 км с поверхностью Земли
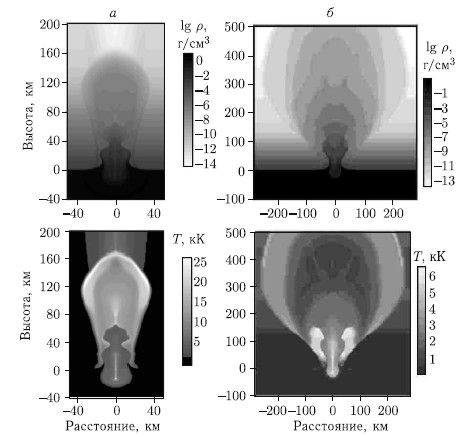
Рис. 8.4. Распределение плотности (верхняя панель) и температуры (нижняя панель) через 5 с (а) и 15 с (б) после удара о Землю каменного тела диаметром 10 км со скоростью 20 км/с
Используя «экспериментальное» значение площади пожара для энергии E = 30 Мт (Тунгусское событие), получим следующие соотношения:
Ar = 30Er, Rf = 3Er1/2 N = 2,9 103Er,
где Ar — площадь воздействия теплового излучения в км2, Rf — радиус зоны пожара в км, N — число жертв, Er — энергия теплового излучения в Мт, которая для больших взрывов примерно составляет 30–40 % от энергии взрыва E [Glasstone and Dolan, 1977] или энергии ударника Ek.
При ударе метеороида и его фрагментов о поверхность твердого тела со скоростью более 15 км/с происходит испарение ударника и поверхности мишени. При расширении в вакуум характерный размер излучающей области Rf составляет примерно 10–15 размеров ударника [Melosh et al., 1993; Немчинов и др., 1998]. Время излучения порядка Rf/V, где V — скорость удара о Землю. Излучательная эффективность в вакууме ? зависит от скорости ударника, но в среднем очень мала (? ? 10-4–10-2). Такие значения применимы при ударах об астероиды, планеты и их спутники, лишенные атмосферы, например о Луну [Ortiz et al., 2000]. Именно эти значения приняты в программе СММ для излучения факела. Однако в условиях весьма плотной атмосферы Земли они сильно преуменьшают реальную излучательную эффективность. Во-первых, наличие атмосферы сильно сдерживает разлет паров и скорость их охлаждения, увеличивает их плотность и оптическую толщину. Во-вторых, воздух нагревается в ударной волне, генерируемой при расширении паров, и сам излучает.
Характерная скорость ударной волны, при которой интенсивность излучения еще достаточно высока, составляет ? 6 км/с. Даже при ударе в воду скорость расширения паров, по крайней мере вблизи места удара, настолько велика, что ударная волна в воздухе интенсивно излучает. Так, даже при скорости ударной волны 5 км/с давление в ней составляет ? 25 ГПа. Согласно ударной адиабате, приведенной в работе [Stewart and Ahrens, 2005], температура сжатых в ударной волне воды или льда составляет 1700 К, и излучение сжатой воды не интенсивно. В то же время, согласно адиабате разгрузки, полученной в работе [Stewart and Ahrens, 2005], скорость паров воды при разгрузке от таких давлений до близких к атмосферным составляет ? 6 км/с. При таких скоростях температура воздуха за ударной волной достигает 10 000 К [Кузнецов, 1965] и излучение весьма интенсивно. Поэтому для оценок следует использовать значение излучательной эффективности, найденное при ядерных испытаниях, а именно 30–50 % [Glasstone and Dolan, 1977], или хотя бы значения порядка 10 %, полученные при расчетах входа в атмосферу тел размером 1–100 м [Nemtchinov et al., 1997b].
В программе СММ учитывается кривизна поверхности Земли, ограничивающая распространение вдоль нее излучения, но не учитывается тот факт, что излучающая область поднимается вверх, причем для больших тел достаточно быстро, тем самым увеличивая облучаемую поверхность. Кроме того, прозрачность стратосферы выше, чем тропосферы. Согласно оценкам по программе СММ, в варианте 1 на расстоянии 15 км импульс светового излучения Er составляет 400 Дж/см2, в варианте 2 на расстоянии 25 км — 900 Дж/см2. В то же время по нашим оценкам на этих же расстояниях в варианте 1 величина Er составляет 5 кДж/см2, а в варианте 2–10 кДж/см2, что на порядок выше, чем по программе СММ. Согласно [Glasstone and Dolan, 1977], одежда загорается при Er = 100 Дж/см2, трава — при 38 Дж/см2. Таков же примерно порог ожогов 3-й степени. Поэтому расстояние поражения световым излучением намного больше, чем оценивается по программе СММ, и лимитируется в основном погодными условиями (прозрачностью атмосферы, облачностью и т. д.).
Отметим еще, что защита от несчастных случаев при пожарах мерами гражданской обороны с увеличением энергии и площади облучения становится все более трудной, так как могут возникать дополнительные эффекты (например, «огненный смерч» [Андрианов и др., 2003]).
| <<< Назад Глава 8 Последствия падений крупных небесных тел на землю |
Вперед >>> 8.2. Последствия ударов о поверхность |
- РАЗДЕЛ 3. Вопросы, связанные с реинтродукцией
- Некоторые проблемы, связанные со стереоскопическим зрением
- Цветы на стволах и причины этого явления
- Экспериментальные подходы к изучению роли мозга в эмоциональных проявлениях
- Ошибки, связанные с непредсказуемостью окружающей среды и «недоброжелательностью»
- А. Г. Петренко К истории появления животноводческих основ в среднем Поволжье и Предуралье
- Электрические явления в клетке
- § 13. Явления природы. Физические явления
- Ламарковские и квазиламарковские явления в эволюции
- Происхождение небесных тел
- § 14. Химические явления. Горение
- 303. Влияют ли приливо-отливные явления на поведение рыб?
