Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

С помощью спектроскопа[67] можно было оценить, насколько быстро движутся звезды в той или иной галактике. Проведя такую оценку, астрономы получили чрезвычайно загадочный результат. Современное решение этой загадки я оставлю до главы 14, а пока просто расскажу, что получилось.

Астрономы измеряют, насколько быстро вращаются галактики, при помощи эффекта Доплера. Суть этого эффекта такова: если свет какой-то определенной длины волны излучается движущимся источником, то его длина волны изменяется в соответствии со скоростью источника. Такой же эффект наблюдается у звуковых волн; классический пример — то, как меняется звук сирены автомобиля скорой помощи после того, как сам автомобиль проедет мимо. Физик Кристиан Доплер проанализировал этот эффект на основе ньютоновой физики в 1842 году в работе о двойных звездах. Релятивистская версия предсказывает тот же базовый результат, но с количественными отличиями. Конечно, свет содержит в себе множество длин волн, но спектроскопия позволяет запечатлеть конкретные длины волн в виде темных линий в спектре. Если источник света движется, все эти линии сдвигаются в одну сторону, и по величине сдвига несложно рассчитать скорость источника.

В случае галактик для этой цели обычно используется альфа-линия водорода H?. Для неподвижного источника она располагается в темно-красной зоне видимого спектра, а возникает при переходе электрона в атоме с третьего снизу энергетического уровня на второй снизу. Водород — самый распространенный химический элемент во Вселенной, так что его альфа-линия, как правило, хорошо видна.

Можно даже — для не слишком далеких галактик — последовательно измерить скорость вращения на разных расстояниях от центра галактики. Эти измерения позволяют определить кривую вращения галактики, и оказывается, что скорость вращения зависит только от расстояния до центра. С хорошим приближением галактика ведет себя как серия концентрических колец, каждое из которых вращается жестко, но со скоростью, которая может различаться от кольца к кольцу. Это напоминает предложенную Лапласом модель колец Сатурна (глава 6).

В этой модели законы Ньютона позволяют вывести ключевую математическую закономерность: формулу, которая связывает скорость вращения на заданном радиусе и суммарную массу внутри этого радиуса. (Звезды движутся настолько медленно по сравнению со скоростью света, что в релятивистских поправках, по общему мнению, нет необходимости.) Согласно этой формуле, полная масса галактики в пределах от центра до заданного радиуса равняется этому радиусу, умноженному на квадрат скорости обращения звезд на этом расстоянии и деленному на гравитационную постоянную[68]. Эту формулу можно переписать так, чтобы она выражала скорость обращения звезд в галактике на заданном расстоянии от центра: она равна корню квадратному из полной массы внутри этого радиуса, умноженной на гравитационную постоянную и деленной на радиус. Эта формула в любом варианте называется уравнением Кеплера для кривой вращения, поскольку ее можно вывести также непосредственно из законов Кеплера.

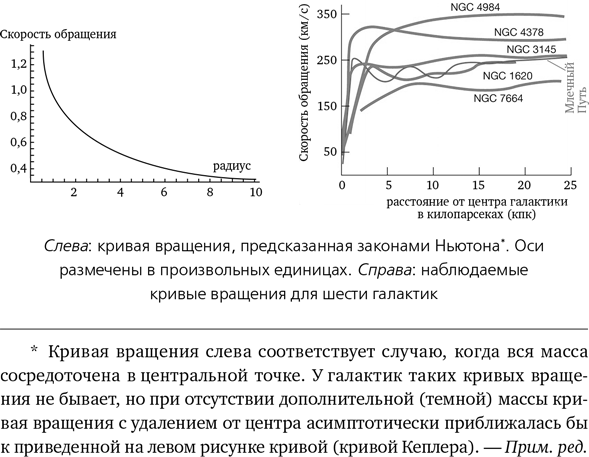
Распределение массы трудно измерить непосредственно, но в одном аспекте предсказание никак не зависит от подобных соображений: речь идет о поведении кривой вращения на достаточно больших радиусах. С приближением радиуса к наблюдаемому радиусу галактики полная ее масса внутри этого радиуса становится почти константой и равной полной массе галактики. Поэтому при достаточно большом радиусе скорость обращения обратно пропорциональна квадратному корню из радиуса. Рисунок слева представляет собой график этой формулы, значение которой с ростом радиуса спадает до нуля.

Для сравнения: справа приведены наблюдаемые кривые вращения для шести галактик, в том числе нашей. Вместо того чтобы спадать до нуля, скорость обращения звезд растет с расстоянием от центра, а затем остается примерно постоянной.

Упс!