Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

Эти теории формирования спиральных рукавов не теряли актуальности более 50 лет. Однако недавние математические достижения позволяют предположить нечто совершенно иное. Ключевой пример здесь — спиральные галактики с перемычкой; в этих галактиках имеются классические спиральные рукава, но есть и прямая перемычка в середине. Типичный пример такой галактики — NGC 1365.

Один из способов хотя бы чуть-чуть разобраться в галактической динамике — создать модель системы n тел с большими величинами n и моделировать поведение каждой звезды в ответ на гравитационное воздействие всех остальных. Для реалистичного применения этого метода требуется несколько сотен миллиардов тел, но такие вычисления вряд ли реальны, поэтому на самом деле используются более простые модели. Один из таких подходов дает объяснение регулярной структуре спиральных рукавов. Как ни парадоксально, причиной их возникновения является хаос.

Если вы считаете, что «хаос» — это всего лишь красивое слово для обозначения «случайности», вам трудно понять, как регулярная структура может иметь хаотическое объяснение. Все дело в том, что хаос, как мы уже видели, на самом деле не случаен. Он возникает там, где действуют детерминистские правила, и вследствие их работы. В каком-то смысле эти детерминистские правила играют роль скрытых закономерностей, лежащих в основе хаоса. В спиральных галактиках с перемычкой отдельные звезды движутся хаотично, но при их движении галактика сохраняет общую спиральную форму. По мере того как одни звезды уходят из сгущений вдоль спиральных рукавов, их место занимают другие. Возможность существования закономерностей в хаотической динамике — предупреждение тем ученым, кто считает, что регулярный результат должен иметь столь же регулярную причину.

В конце 1970-х годах Джордж Контопулос со своими сотрудниками смоделировали спиральную галактику с перемычкой, взяв за основу жестко вращающуюся центральную перемычку и использовав модели n тел для определения динамики звезд в спиральных рукавах, движимых вращением центральной перемычки. Морфология перемычки в этой модели постулируется, но работа модели показывает, что наблюдаемая форма разумна. В 1996 году Дэвид Кауфман и Контопулос открыли, что внутренние части спиральных рукавов, как будто свисающие с концов перемычки и закручивающиеся вслед за ней, состоят из звезд, которые движутся по хаотическим орбитам. Центральная область галактики, в первую очередь перемычка, вращается как единое целое; это явление называется коротацией[66]. Звезды, образующие внутреннюю область спиральной структуры, относятся к так называемому «горячему населению» галактики, они движутся хаотически и то входят в центральную область, то вновь выходят из нее. Внешние части рукавов составляют звезды, движущиеся по более правильным орбитам.

Вращающаяся перемычка создает гравитационный ландшафт, очень напоминающий ландшафт в задаче Пуанкаре о двух с половиной телах, но геометрия там иная. По-прежнему существует пять точек Лагранжа, где пылинка будет покоиться в системе отсчета, вращающейся вместе с перемычкой, но расположены они иначе, в виде креста. В модели, о которой идет речь, в настоящее время рассматривается около 150 000 пылинок — других звезд — и все они воздействуют друг на друга, но не на перемычку. Математически это модель системы из 150 000 тел в фиксированном вращающемся гравитационном ландшафте.

Три из пяти точек Лагранжа — L₃, L₄ и L₅ — стабильны. Другие две — L₁ и L₂ — характеризуются как нестабильности типа «седло» и располагаются вблизи концов перемычки, которая изображена в форме вытянутого эллипса. А теперь нам не обойтись без небольшой дозы нелинейной динамики. С равновесиями седловидного типа связаны две особые многомерные поверхности, так называемые стабильная и нестабильная трубки. Это традиционные названия, хотя в некоторых случаях они могут ввести человека в заблуждение. Они не означают, что связанные с ними орбиты стабильны или нестабильны; они указывают лишь направление потока, определяющего эти поверхности. Пылинка, помещенная в стабильную трубку, будет двигаться к седловидной точке как будто под действием силы притяжения; пылинка, помещенная в нестабильную трубку, двинется прочь как будто под действием отталкивающей силы. Частица, помещенная куда-то в иное место, будет следовать по траектории, сочетающей оба типа движения. При рассмотрении именно этих поверхностей Пуанкаре первоначально открыл хаос в задаче двух с половиной тел. На пересечении этих трубок возникает гомоклиническое плетение.

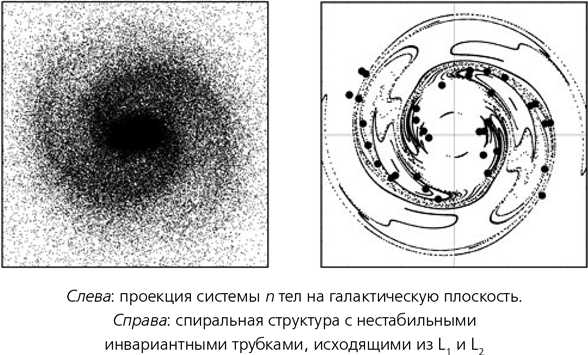
Если бы в этой задаче рассматривалось только положение в пространстве, то стабильная и нестабильная трубки представляли бы собой кривые, пересекающиеся в точке седловины. В горизонталях возле L₁ и L₂ имеется крестообразная прореха, показанная в увеличенном виде на рисунке справа. Эти кривые проходят через середину прорехи. Однако в астрономических орбитах речь идет не только о положении в пространстве, но и о скорости. Вместе эти величины определяют многомерное пространство, известное как фазовое пространство. Здесь два измерения, характеризующие положение в пространстве и непосредственно показанные на рисунке, необходимо дополнить еще двумя измерениями скорости. Фазовое пространство четырехмерно, а стабильные и нестабильные трубки представляют собой двумерные поверхности и показаны на рисунке справа в виде трубок, помеченных стрелками: S — стабильная трубка, U — нестабильная.

Там, где эти трубки встречаются, они работают как ворота между областью коротации и тем, что в нее не входит, то есть внешней областью. Звезды могут проходить по ним как внутрь этой области, так и наружу, в направлениях, указанных стрелками; кроме того, проходя, при этом они могут хаотически переходить (или не переходить) из одной трубки в другую. Некоторые звезды из внутренней области коротации проходят через эти ворота и уносятся прочь по трубке, помеченной буквой U, внизу справа. И здесь вступает в игру явление, известное как «липкость». Несмотря на то что динамика хаотична, звезды, выходящие через ворота, держатся вблизи нестабильной трубки долгое время — возможно, дольше, чем проживет Вселенная. Обобщая, получим, что звезды вытекают потоком возле L₁, а затем следуют по направленной наружу ветви нестабильной трубки, которая здесь поворачивает по часовой стрелке. То же происходит и в L₂, расположенной напротив L₁, или на 180° относительно центра галактики от нее.

Со временем многие из этих звезд вновь проникают в область коротации, и все повторяется заново, хотя и не через равные интервалы времени из-за влияния хаоса. Поэтому то, что мы увидим, — это пара спиральных рукавов, выходящих под углом из концов перемычки, в то время как вся структура равномерно вращается как целое. Отдельные звезды не остаются постоянно в рукавах на одних и тех же местах. Скорее они напоминают искры, которые разбрасывает, вращаясь, огненное колесо (вертушка). Вот только искры эти со временем возвращаются к центру, чтобы их разбросало снова, и траектории их меняются хаотически.

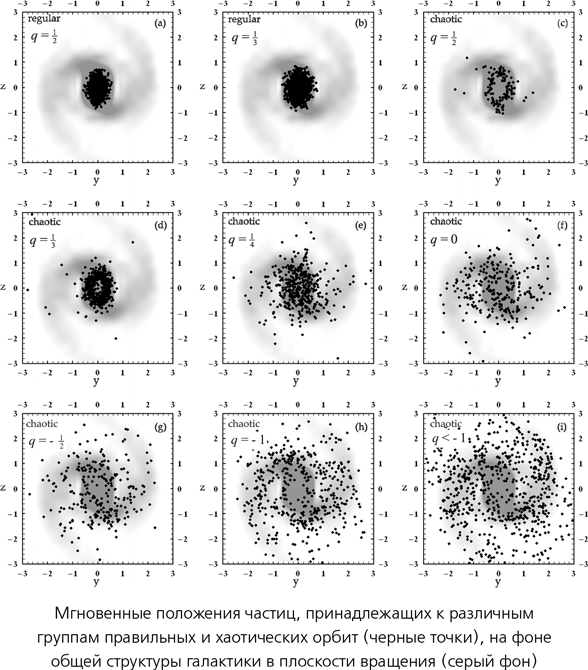
Рисунок слева показывает положение звезд в какой-то произвольный момент времени в модели системы n тел. Хорошо видны два спиральных рукава и центральная перемычка. Рисунок справа показывает нестабильные трубки, которые соответствуют наиболее плотно населенным областям левого рисунка. На следующем рисунке показано, какие части галактики заняты звездами различных групп с правильными и хаотическими орбитами. Правильные орбиты, как можно ожидать, сосредоточены в коротационной зоне; хаотические там тоже имеются, но они доминируют за ее пределами, там, где находятся спиральные рукава.

Имеет смысл сравнить эту теорию с серией скрученных эллипсов на рисунке ранее. Эллипсы там выстроены по определенной схеме, чтобы в результате получилась нужная нам структура. Однако реальная динамика n тел не дает эллиптических орбит, поскольку все тела в системе оказывают друг на друга возмущающее действие, так что предложенная схема не имеет реального смысла, если только не является разумной аппроксимацией другой, более реальной схемы. Хаотическая модель действительно встраивает в систему центральную перемычку в качестве предварительного условия, но все остальное вытекает из самой обычной динамики n тел. В результате мы получаем не только хаос — как и следовало ожидать, — но и спиральную структуру, созданную хаосом. Из этого можно извлечь важный урок: принимайте математику всерьез и закономерности не заставят себя долго ждать. С другой стороны, выдумывая искусственные закономерности на пустом месте, рискуешь получить в ответе чепуху.

То, что вездесущий хаос играет роль в формировании спиралей в спиральных галактиках с перемычками, подтверждается и другими данными. К примеру, в таких галактиках часто встречаются звездные кольца очень правильной формы, часто парные, перекрывающиеся между собой. Идея опять же в том, что в таких галактиках вездесущий хаос выстраивает многие звезды вдоль нестабильных трубок точек Лагранжа L₁ и L₂ на концах перемычки. На этот раз мы рассматриваем также и стабильные трубки, вдоль которых звезды возвращаются к воротам и обратно в центральную часть. Эти трубки тоже обладают «эффектом прилипания».

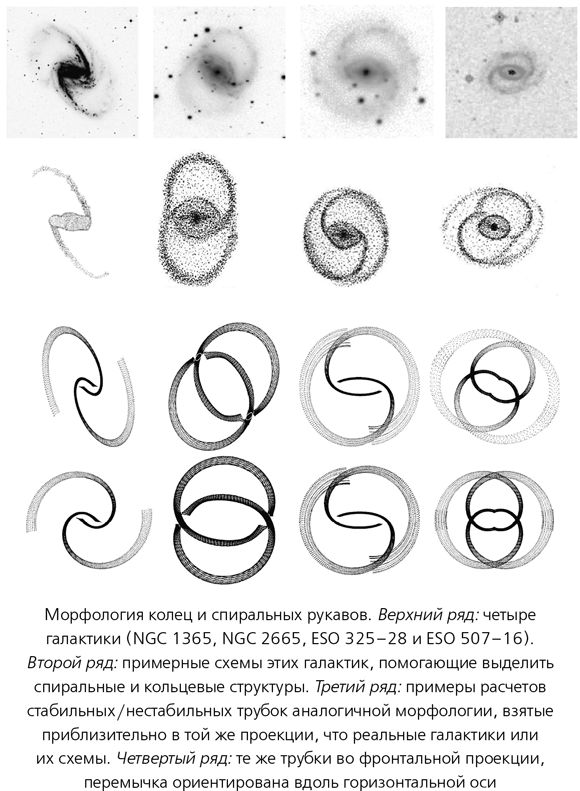
В верхнем ряду на рисунке выше показаны четыре типичных примера галактик с кольцами. Во втором ряду вы можете видеть схематические рисунки, подчеркивающие спиральные и кольцеобразные структуры в них. В третьем ряду представлены аналогичные примеры, полученные при помощи математической модели. В четвертом ряду эти же примеры показаны во фронтальной проекции, а не под углом.