Книга: Мир математики. т.30. Музыка сфер. Астрономия и математика

Древняя задача определения долготы

Из Гибралтара, на юге Пиренейского полуострова, на родину отплывает пять английских кораблей. Туманной ночью 22 октября 1701 года в условиях плохой видимости, неподалеку от архипелага Силли (к юго-западу от Англии) адмирал Клаудесли Шовелл собирает офицеров, чтобы определить координаты кораблей и дальнейший курс. Все сходятся на том, что нужно следовать на север. Однако матрос с флагманского корабля «Содружество» сообщает капитану, что, по его подсчетам, корабли следуют неверным курсом, так как их координаты были определены неверно. На борту поддерживается строжайшая дисциплина, и матроса немедленно вешают за нарушение субординации. Спустя несколько часов «Содружество» налетает на огромные подводные камни близ архипелага Силли и тонет за несколько минут.

Эта же судьба постигает еще три корабля, и лишь одному удается спастись. При кораблекрушении погибло более 2 тысяч человек.

Это далеко не единственная история подобного рода. Прокладывать курс вдали от побережья было очень сложно, поскольку моряки не умели точно вычислять координаты корабля в открытом море. Конечно, любой опытный моряк умел определять широту по высоте Полярной звезды (в Северном полушарии) или по расположению Солнца в полдень. Однако с долготой все было намного сложнее.

Угловая высота Полярной звезды над горизонтом равна широте корабля.

Этим же свойством обладают и другие звезды, в частности Южный Крест или Пояс Ориона, однако оценить их положение на небе несколько сложнее. Аналогично, широту нетрудно определить по Солнцу в момент прохождения меридиана в 12 часов по солнечному времени, когда тени предметов будут самыми короткими.

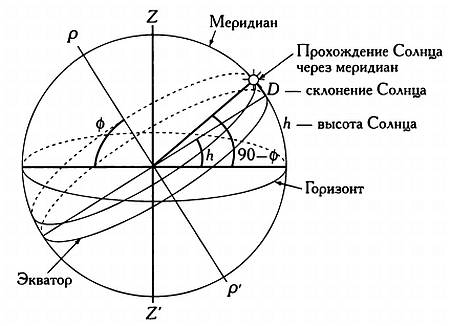
Чтобы определить широту места, нужно измерить высоту Солнца над горизонтом А, зная склонение Солнца в день наблюдений.

С помощью простейшего инструмента (квадранта или поперечного жезла) или более современного приспособления (секстанта или октанта) несложно измерить высоту Солнца над горизонтом в момент, когда оно пересекает меридиан север — юг, то есть когда оно находится в наивысшей точке над горизонтом. Этот угол, как показано на рисунке дальше, равен А = 90° — ф + D, склонение Солнца в любой день года можно узнать из астрономического ежегодника. Имеем ф = 90°— A + D.

Высота Солнца в момент прохождения местного меридиана равна 90 — ф (где ф — широта) с поправкой на склонение Солнца, которое может быть положительным (летом и весной) или отрицательным (зимой и осенью).

Однако определить долготу совсем не просто. Христофор Колумб в 1492 году попытался достичь Индии, следуя вдоль параллели с момента отплытия с Канарских островов. Широта его кораблей была постоянной, и Колумб не достиг Японии только потому, что путь ему преградила Америка. При таком выборе курса решения задачи о долготе удалось избежать. Но если бы корабли Колумба не достигли Америки, участники экспедиции погибли бы, поскольку Колумб преуменьшил размеры Земли, и когда на горизонте показалась земля, запасы провианта уже подходили к концу. Колумбу повезло…

Почему же определить долготу так сложно? Как мы уже говорили, в силу вращения Земли ось вращения и экватор определяются однозначно. Окружности, параллельные экватору, имеют разные размеры, но обладают одним общим свойством: все они меньше экватора. Однако меридианы, представляющие собой большие круги земной сферы, проходящие через ее полюса, имеют совершенно одинаковую длину, и нулевой меридиан выбирается только из соображений удобства. Основная проблема заключается в том, чтобы определить угловое расстояние из любой точки земной поверхности до этого меридиана, который выбран не из астрономических, а из политических соображений. В этом и заключается основная проблема при определении долготы. Несколько веков назад, когда корабли отправлялись в плавание, моряки располагали лишь примитивными методами определения координат. Они обычно определяли пройденное расстояние, выбрасывая за корму веревку и подсчитывая число узлов, ушедших за борт, в определенный интервал времени. Измерив этот интервал с помощью примитивных песочных часов, моряки вычисляли мгновенную скорость корабля и на основе этого значения примерно оценивали координаты. Однако скорость судна изменялась в зависимости от ветра, течений и других факторов. Иными словами, определить точное положение корабля в открытом море было практически невозможно. Путешествия длились месяцами, недостаток витамина С угнетал сердечно-сосудистую систему, моряки страдали от цинги. Власти всех морских держав были озабочены проблемой определения долготы, которая более 300 лет волновала умы великих ученых.

Как мы уже объясняли, 15° долготы эквивалентны одному часу, или, что аналогично, 1 градус долготы эквивалентен 4 минутам времени. К примеру, на экваторе, где длина земной окружности наибольшая, это расстояние будет равно примерно 111 км. Иными словами, ошибка в одну минуту соответствовала отклонению примерно на 27 километров. К югу или к северу от экватора расстояние, соответствующее одному градусу долготы, уменьшается, что также вносит неточность.

После нескольких месяцев, проведенных в открытом море, определить местонахождение корабля было невозможно. Из-за этого капитаны опасались отклоняться от более или менее известных маршрутов, что приводило к скоплениям судов в определенных регионах и упрощало жизнь пиратам. К примеру, в 1590 году португальский корабль «Мадре де Деуш» был атакован английской эскадрой, которая захватила ценный груз стоимостью полмиллиона фунтов, что в то время составляло половину всего бюджета английского министерства финансов. Задача определения долготы требовала незамедлительного решения.

Учитывая склонность капитанов следовать известным маршрутам, в XVIII веке был предложен любопытный проект. Организаторы проекта хотели поставить на якорь в Атлантическом океане по кораблю каждые 600 миль. Команды этих кораблей должны были стрелять из пушек и запускать фейерверки, видимые на расстоянии в 100 миль, и тем самым указывать курс капитанам других судов. Целью авторов проекта (впрочем, нереализованного) было создание безопасной морской «автомагистрали».

Испанские короли Карл V и Филипп II, король Великобритании Георг II и французский король Людовик XIV потратили много сил на поиски решения. Торговля с Вест-Индией, военные экспедиции, желание открывать новые земли привели к тому, что роль мореходного дела возросла, и, как следствие, увеличилось число кораблекрушений, уносивших множество жизней и ценного груза. Из-за нерешен ной задачи о долготе морские карты до XVII века грешили значительными неточностями. Составлять их вообще было непросто, из-за чего возникали серьезные споры о принадлежности территориальных вод. Все это объясняет, почему многие острова в Океании были открыты по два и даже по три раза. Мореплаватель открывал остров, не нанесенный на карту, и объявлял его собственностью своего короля. Несколько лет спустя другой мореплаватель вновь «открывал» этот же остров и отмечал его на морской карте в другом месте. Впоследствии это приводило к проблемам и спорам, особенно между французскими и английскими мореплавателями, которые были искренне уверены, что именно они открыли тот или иной остров.

Наконец было предложено два принципиально разных решения задачи о долготе: астрономическое и механическое. Астрономическое решение основывалось на наблюдениях периодического движения небесных тел с последующим сравнением их положения на небе. Механическое решение заключалось в создании механических часов, позволявших с точностью определять время. Дело в том, что задача определения долготы на самом деле сводится к задаче определения времени: разница во времени эквивалентна разнице в долготе, и требовалось просто точно измерить эту разницу.

Любой достаточно опытный моряк мог определить, когда наступал солнечный полдень, однако для решения задачи этого было недостаточно. Если бы моряк знал, когда наступает солнечный полдень в порту отплытия, то, определив разницу во времени, он смог бы узнать разницу долгот (повторим: один градус долготы соответствует четырем минутам). Требовалось найти способ, позволявший узнавать время в порту отплытия.

Астрономическое решение

Допустим, что наблюдатель находится в центре Земли и у него есть надежные часы.

Сначала он наблюдает прохождение звезды через нулевой меридиан в момент времени t₁ затем Земля поворачивается на некоторый угол, и наблюдатель видит, что эта же звезда проходит через меридиан места в момент времени t₂. Разница во времени t₂ — t₁ соответствует разнице долгот между нулевым меридианом и меридианом места. Так как наблюдатель находится не в центре Земли, а на ее поверхности, он может наблюдать только момент прохождения звезды через меридиан места. Момент прохождения звезды через нулевой меридиан определяется по астрономическим таблицам, после чего, определив разницу во времени, наблюдатель сможет решить задачу о долготе.

Основным решением задачи было наблюдение затмений. Допустим, что наблюдатель находится посреди Атлантического океана и наблюдает лунное затмение.

Если он знает, что затмение произошло в Лондоне в момент времени h₁ а сам он увидел затмение в момент времени h₂ то, определив разницу во времени h₂ — h₁ он сможет вычислить разницу между долготой корабля и долготой Лондона. Основная проблема заключается в том, с какой точностью мореплаватель может определить время h₂ по своим песочным часам. Кроме того, затмения наблюдаются не каждую ночь, а определять долготу требуется как минимум раз в сутки.

В 1514 году Иоханнес Вернер создал метод лунных расстояний, позднее улучшенный. Мы знаем, что Луна каждый час проходит расстояние, примерно равное ее диаметру, то есть половину градуса. Если у нас есть очень точная карта звездного неба, показывающая, когда Луна «касается» различных известных звезд, мы сможем определить, когда это «касание» можно наблюдать с нулевого меридиана. Если наблюдатель определит точный момент времени, в который Луна «касается» звезды, то сможет вычислить разницу во времени между нулевым меридианом и меридианом корабля. Однако время на корабле определяется по неточным песочным часам.

Кроме того, сложная траектория движения Луны была недостаточно хорошо изучена. Метод лунных расстояний стало возможно использовать с удовлетворительной точностью только в середине XVIII века. На тот момент Джон Флемстид провел более 40 тысяч наблюдений Луны и звезд, астроном-наблюдатель Тихо Браге составил прекрасный атлас звездного неба, Галлей подробно изучил взаимное влияние Земли и Луны друг на друга, а Джон Хэдли изобрел квадрант — астрономический инструмент, при использовании которого с помощью зеркал можно было определять угловую высоту небесных тел над искусственным горизонтом в случаях, когда естественный горизонт не виден. На основе квадранта позднее был создан секстант, дополненный небольшим телескопом и обладавший более высокой точностью.

В 1610 году Галилей открыл спутники Юпитера: Ио, Европу, Ганимед и Каллисто, которые впоследствии стали называться галилеевыми спутниками. Их затмения наблюдались с четкой периодичностью, и Галилей предложил решение задачи о долготе, основанное на результатах наблюдений затмений. Однако увидеть спутники Юпитера было непросто даже с обсерватории на берегу, поэтому метод Галилея оказался неприменим на практике. Хотя ученый даже сконструировал специальный шлем с подзорной трубой, упрощавший наблюдение, сам он признавал, что на его точность могло повлиять даже биение сердца наблюдателя. После смерти Галилея и с усовершенствованием телескопов этот метод начали применять на суше для более точного определения долготы и, следовательно, составления более точных карт. Людовик XIV говорил, что «потерял больше земель по вине своих картографов, чем по вине своих врагов».

Еще один метод определения долготы заключался в оценке изменений магнитного поля. Но от этого метода пришлось отказаться, поскольку отклонение магнитного поля зависело не только от места, но и от времени наблюдений.

Галилеевы спутники Юпитера, слева направо: Ио, Европа, Гэнимед, Каллисто.

* * *

* * *

Решение, найденное часовщиком

Требовалось создать точные механические часы, пригодные для мореплавателей. С их помощью моряки смогли бы определять точное время в порту отплытия (с известной долготой). Если бы часы были идеально точными, то достаточно было определить по Солнцу полдень, посмотреть на часы, показывающие время в порту отплытия, и найти разницу во времени. А уж на ее основании очень просто определить долготу корабля. Первые маятниковые часы изготовил Гюйгенс, однако они сохраняли точность лишь в определенных погодных условиях. Следовательно, использовать такие часы в открытом море было нельзя.

Разные страны предлагали премии тому, кто сможет изготовить механические часы необходимой точности: так, король Испании Филипп III пообещал пожизненную пенсию тому, кто решит задачу о долготе; британский парламент во времена правления королевы Анны, в 1714 году, принял Декрет о долготе, согласно которому того, кто решит задачу с погрешностью менее половины градуса (то есть 50 километров на экваторе), ждала премия в 20 тысяч фунтов. Как видите, требуемая точность была очень велика, а огромный размер премии наводит на мысли, что англичане были на грани отчаяния — от решения задачи о долготе зависела экономика всей страны. Чтобы автор решения получил премию, его часы должны были сохранять требуемую точность хода во время плавания до Вест-Индии и обратно. Для контроля был учрежден Совет по долготе, куда вошли глава Гринвичской королевской обсерватории, глава Лондонского королевского общества, морской министр, председатель палаты общин, делегат от вооруженных сил и несколько ученых. Получить премию пытались многие. Мы отметим лишь Джереми Такера: он сконструировал часовой механизм, позднее дополненный двумя усовершенствованиями, которые используются и по сей день. Речь о вакуумной камере со стеклянными стенками и особой системе, благодаря которой часы не останавливались во время завода.

Решение задачи о долготе нашел плотник Джон Гаррисон, который сконструировал первые часы из маленьких латунных деталей, когда ему не было и двадцати лет. Гаррисон дополнил часы таблицей уравнения времени для сравнения фактического и солнечного времени. Он же придумал маятник, состоящий из двух стержней, изготовленных из чередующихся полос различных металлов, чтобы компенсировать воздействие перепадов температуры на точность хода. Однако в морских часах маятнику было не место, поэтому Гаррисон разработал особый механизм, обеспечивавший равномерную передачу энергии от сжатой пружины.

* * *

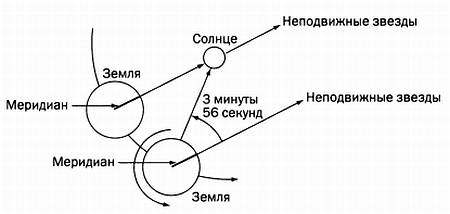
Разница между звездным и солнечным временем.

* * *