Книга: Природа описывается формулами. Галилей. Научный метод.

ПОД ВЛИЯНИЕМ АРХИМЕДА

Будучи учеником Риччи, Галилей попал под косвенное влияние подхода Архимеда к математике. Возможно, какое-то время он признавал представления Аристотеля о том, что математика не может описывать природу в силу своей конечности и что более глубокое познание мира возможно при помощи категории качества, а не количества.

Принцип Архимеда, согласно которому на тело, погруженное в жидкость, действует сила, равная весу вытолкнутой им жидкости, вдохновил его на первое изобретение — маленькие гидростатические весы, позволявшие измерять удельный вес тел.

Первое, очень короткое, эссе Галилея так и называлось — «Маленькие гидростатические весы». Оно было опубликовано в 1586 году и объясняло принцип действия устройства. В нем Галилей утверждал, что вдохновился эпизодом, когда Архимед раскрывает обман с короной царя Гиерона. Галилей совсем не был уверен, что классическое объяснение было истинным:

«Как известно [...], Архимед обнаружил обман ювелира в короне Гиерона, но мы до сих пор не знаем, к какому способу прибег этот великий ученый, чтобы определить это. То, что он, по некоторым источникам, поместил в воду корону, а затем — такие же по весу слитки чистого золота и серебра и по разнице вымещенной воды понял, что к золоту в короне было подмешано серебро, кажется мне, если позволительно так выразиться, весьма грубым и неизящным».

По мнению Галилея, Архимеду для решения задачи понадобилось бы его изобретение — гидростатические весы. Они состояли из двух плечей: на одно подвешивается предмет, который надо взвесить, а на другое ставятся гирьки до момента уравновешивания (см. рисунок). Затем предмет погружается в воду, и его масса вычисляется заново. К разнице этих двух масс применяется принцип Архимеда. Поскольку плотность воды составляет 1 г/см?, надо просто использовать формулу плотности р = m/V.

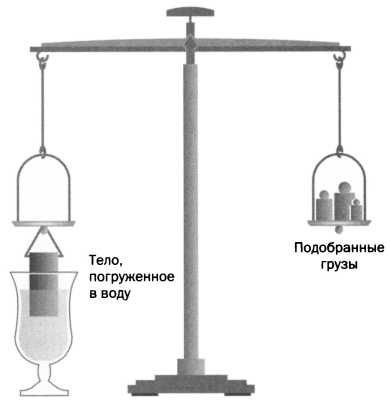
Гидростатические весы позволяют сравнить плотности тел и таким образом определить их удельный вес.

Риччи, как и его учитель, считал математику практической дисциплиной, которая могла использоваться во множестве различных областей, от военного дела до архитектуры. Такая точка зрения очень отличалась от пифагорейских и платоновских представлений, по которым реальность заключалась главным образом в числах. По мнению пифагорейцев, числа определяли структуру природных явлений, и изучение математических соотношений являлось путем познания мира.

Галилей изучал математику в тесной связи с практикой и наблюдениями. Свое восхищение Архимедом он выразил в том числе в таких строках: «...тем, кто... читал и изучал искуснейшие изобретения столь божественного человека, ... слишком ясно, насколько все остальные ученые были ниже Архимеда...»