Книга: Природа описывается формулами. Галилей. Научный метод.

ГАЛИЛЕЙ-ЭКСПЕРИМЕНТАТОР

В своих «Беседах...» Галилей подробно описывает опыт, в котором он подошел к решению задачи о падении тел с помощью наклонной плоскости. Галилей установил, что пройденный путь пропорционален квадрату времени. Эту пропорцию до сих пор изучают в школах. Сейчас ее записывают следующим образом: расстояние (s) и время (t) при равноускоренном движении соотносятся как s = ?gt?, где g — ускорение свободного падения, значение которого на уровне моря равно 9,81 м/с?.

«Вдоль узкой линейки или, лучше сказать, деревянной доски длиной около двенадцати локтей, шириной пол-локтя и толщиной около трех дюймов был прорезан канал шириной немного больше одного дюйма. Канал этот был прорезан совершенно прямым и, чтобы сделать его достаточно гладким и скользким, оклеен внутри возможно ровным и полированным пергаментом; по этому каналу мы заставляли падать гладкий шарик из твердейшей бронзы совершенно правильной формы. Установив изготовленную таким образом доску, мы поднимали конец ее над горизонтальной плоскостью, когда на один, когда на два локтя, и заставляли скользить шарик по каналу, отмечая [...] время, необходимое для пробега им всего пути; повторяя много раз один и тот же опыт, чтобы точно определить время, мы не находили никакой разницы даже на одну десятую времени биения пульса. Точно установив это обстоятельство, мы заставляли шарик проходить лишь четвертую часть длины того же канала; измерив время его падения, мы всегда находили самым точным образом, что оно равно всего половине того, которое наблюдалось в первом случае. Производя далее опыты при различной иной длине пути, сравнивая время прохождения всей линейки со временем прохождения половины, двух третей, трех четвертей или любых иных частей ее и повторяя опыты сотни раз, мы постоянно находили, что отношение пройденных путей равно отношению квадратов времени их прохождения при всех наклонах плоскости, то есть канала, по которому скользил шарик».

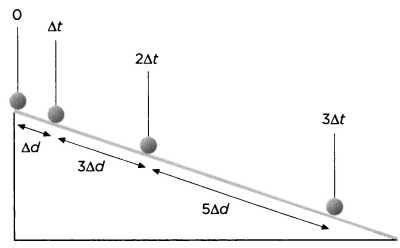
На рисунке показано, что за одну единицу времени шар проходит одну единицу расстояния, за две единицы времени — 4 (= 1 + 3) единицы расстояния (или за половину единицы времени — четверть расстояния); за три единицы времени — 9 (= 1 + 3 + 5) единиц расстояния и так далее. Таким образом, пройденное расстояние всегда равно квадрату временных промежутков (1?, 2?, З?,...).