Книга: Естествознание. Базовый уровень. 10 класс

§ 13 Пространство и расстояние

§ 13 Пространство и расстояние

Итак, мы выяснили, что интуитивно каждый человек понимает, что такое пространство. А как обстоит дело с более строгой научной характеристикой этого понятия? То пространство, с которым мы привыкли иметь дело в обыденной жизни, где мы измеряем длины, расстояния и размеры, называется евклидовым пространством по имени греческого математика Евклида, жившего около III в. до н. э. и создавшего аксиомы геометрии – науки об измерениях в пространстве. Геометрия Евклида была единственно признанной до появления работ российского математика Н. И. Лобачевского и немецкого математика Г. Римана.

Системы координат.

Обычно для описания пространства используется наиболее простая система координат, называемая прямоугольной. Её ещё называют декартовой по имени французского учёного Рене Декарта, который впервые предложил её в 1637 г. (рис. 33, 34). В этой системе определяется точка, которая называется началом координат или точкой отсчёта.

Рис. 33. Рене Декарт

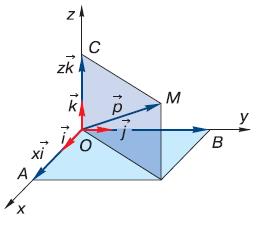
Рис. 34. Декартова система координат

В этой точке пересекаются три взаимно перпендикулярные прямые, одна из которых называется осью абсцисс, или осью х, вторая – осью ординат (осью у), а третья – осью аппликат (осью z). Очевидно, что в том пространстве, где мы обитаем, большее число взаимных перпендикуляров построить невозможно. Поэтому наше пространство называют трёхмерным. В физике и математике часто рассматриваются пространства с большим числом измерений: от четырёхмерного пространства-времени Минковского до пространств, имеющих бесконечное число измерений в квантовой физике. Однако наглядно представить себе пространство, где имеется больше трёх измерений, невозможно. Можно, наоборот, уменьшить число координат до двух, ограничившись только осями абсцисс и ординат, и получить систему координат на плоскости. Мы уже имели дело с такой системой в § 8, когда знакомились с построением графиков. Полная же система координат, описывающая положение любой точки в пространстве, является трёхмерной. Для того чтобы определить местонахождение этой точки, надо знать три числа, обозначающие проекции[6] этой точки на оси абсцисс, ординат и аппликат (x, у, z). Сумму величин p^?=xi^?+ yj^?+ zk^?называют вектором, определяющим положение точки в пространстве. Поскольку оси координат представляют собой бесконечные прямые и каждая из них распространяется в обе стороны от начала координат, то x, y и z могут иметь как положительные, так и отрицательные значения.

Расстояние между двумя точками в евклидовом пространстве определяют с помощью теоремы Пифагора. Глядя на рисунок, можно легко убедиться в том, что на плоскости расстояние между двумя любыми точками равно:

??х²+ y²,

а в пространстве:

??x² + у² + z².

В некоторых случаях используют не прямоугольные, а другие системы координат, например цилиндрическую и сферическую. Цилиндрическая система строится следующим образом. Допустим, нам нужно определить положение точки М (рис. 35, А). Пусть в пространстве задана декартова прямоугольная система координат Oxyz и R – расстояние от точки М до координатной оси Oz.

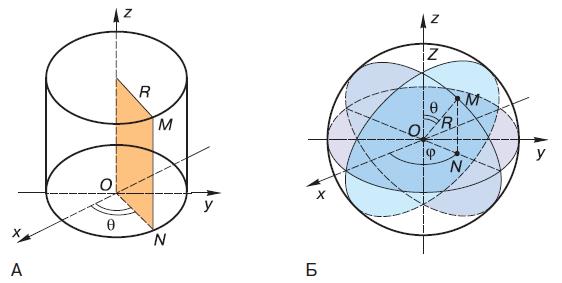
Рис. 35. Цилиндрическая (А) и сферическая (Б) системы координат

Тогда одной из координатных поверхностей (R = const), проходящих через точку М, является цилиндрическая поверхность вращения с осью Oz и радиусом R (поэтому координаты точки М называются цилиндрическими). Если при этом 0 – угол, который плоскость, проходящая через точку М и координатную ось Oz, образует с координатной плоскостью Oxz, то цилиндрическими координатами точки М является упорядоченная тройка чисел (R; ?; Z), где Z – проекция М на ось Oz.

Сферическая система координат используется в астрономии и навигации. Для определения положения точки необходимо знать её расстояние от начала координат – центра сферы (т. е. радиус сферы) и два угла (рис. 35, Б). Попробуйте сами построить такую систему, воспользовавшись приведённым рисунком.