Книга: Самая главная молекула. От структуры ДНК к биомедицине XXI века

Об узлах

Об узлах

Всякий знает, что такое узел. Мы каждый день завязываем множество узлов. Обычно мы делаем это так:

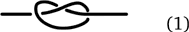
Не правда ли, самый простой узел? Ну а это что такое?

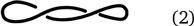
Немного подумав, благоразумный читатель ответит: «Просто закрученное в жгут кольцо. К узлам эта штука отношения не имеет. Зря это здесь нарисовано». Нет, я не зря изобразил жгут – он, как и само кольцо, из которого жгут образован,

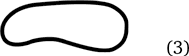
имеет не меньше, а, пожалуй, даже больше прав именоваться узлом, чем фигура (1).

Математик назовет фигуру (2) или фигуру (3) тривиальным узлом. А первую вообще откажется считать узлом.

«Ох, уж эти математики! – думаете, наверное, вы. – Вечно они все запутывают». Пожалуй, я бы согласился с вами. Я не математик и часто сам думаю точно так же. Но в данном случае я решительно с вами не согласен.

Можно, конечно, называть фигуру (1) узлом, но попробуйте четко объяснить, чем она отличается от такой:

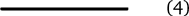
Ведь фигуру (1) всегда можно распутать, и цепь вернется в исходное состояние. Этого нельзя сделать только в одном случае – если концы цепи бесконечно длинные. Поэтому лучше вообще избавиться от концов:

Попробуйте-ка теперь распутать! Каждому ясно, чем фигура (5) отличается от фигуры (3): их никаким образом нельзя перевести одну в другую, не порвав цепь. Узел (5) называют трилистником или клеверным листом, так как его можно переделать вот так:

Думаю, теперь вы согласитесь, что понятие узла имеет строгий смысл только для замкнутых цепей, хотя в домашнем обиходе вы можете продолжать называть узлами фигуры типа (1), если вам это очень нравится.

Итак, мы уже знаем два узла – тривиальный (среди узлов он занимает то же положение, что и нуль среди чисел) и трилистник, (5) или (6). Следующий после трилистника по сложности узел называется восьмеркой. Он выглядит так:

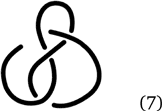
А это что такое?

Представьте себе, что такая штука сделана из веревки. Можно ли, не разрывая веревку, перевести ее в простое кольцо (тривиальный узел), или в трилистник, или в восьмерку? Или нельзя? Иными словами, до какого простейшего вида этот узел можно распутать?

Первым всерьез заинтересовался узлами британский физик и математик П. Тэйт. Это было в 1860-х годах. Тогда физики (как, впрочем, и сейчас) хотели понять, как устроены простейшие частицы материи. Тогда, как и сейчас, они думали, что частицы могут представлять собой вихри электричества. Как-то в письме к Тэйту Максвелл написал: «А что, если этот вихрь будет заузлен?» И нарисовал трилистник.

Тэйт имел склонность к абстрактным математическим построениям. Он стал думать: какие еще бывают узлы? Но вскоре совсем забыл о частицах (будто знал, что с ними и через полтораста лет не разберутся) и стал просиживать долгие часы с веревкой, завязывая всевозможные узлы. Тэйт составил первую таблицу узлов. В ней он последовательно разместил те узлы, которые смог придумать. В дальнейшем была проведена полная «инвентаризация» всех узлов, имеющих менее десяти пересечений на их проекциях. Таких узлов набралось 84. Часть из них изображена на рис. 35.

Узлы располагают по возрастанию минимального числа пересечений на их проекции. Для трилистника это число равно трем, для восьмерки – четырем. Если есть несколько разных узлов с одинаковым числом пересечений, то они группируются в таблице вместе и каждый получает, кроме обозначения числа пересечений, еще и дополнительный индекс.

Тэйт заинтересовал проблемой узлов знакомых математиков. Повозившись с узлами лет 60, они довольно здорово наловчились распутывать сложные узлы и в 1928 году придумали инвариант узла.

Инвариант узла – это такое алгебраическое выражение, значение которого не меняется, как бы вы ни запутывали узел. Умение вычислять инвариант позволяет в принципе распутать любой узел. Достаточно определить инвариант, а затем сравнить его со значениями инвариантов, вычисленными для узлов, вошедших в таблицу. Наиболее удобным инвариантом оказались так называемые полиномы (многочлены) Александера ?(t). Для тривиального узла ?(t) = 1. Для трилистника ?(t) = t²—t + 1. Для восьмерки ?(t) = t²–3t + 1 и т. д. Таким образом, каждый узел характеризуется не отдельным числом, а целым алгебраическим выражением, в котором есть некая переменная, не имеющая специального смысла.

Если вы умеете вычислять полином Александера, то довольно быстро убедитесь, что фигура 7 – это на самом деле тривиальный узел, только сильно запутанный. Возможно, вы этого делать не умеете, и придется повозиться, чтобы в этом убедиться. Или вы должны будете мне просто поверить.

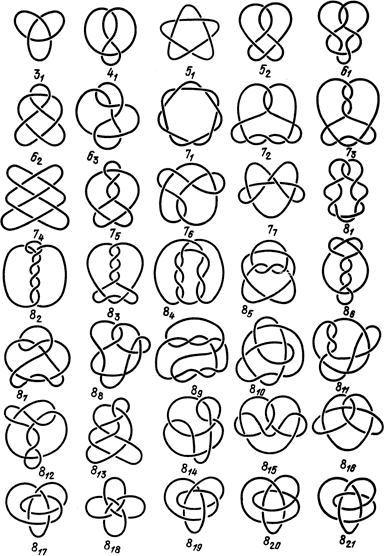
Рис. 35. Узлы