Книга: Высший замысел
8. Высший замысел
| <<< Назад 7. Кажущееся чудо |
Вперед >>> Словарь терминов |
8. Высший замысел
В этой книге мы рассказали, как закономерности в движении астрономических тел, таких как Солнце, Луна и планеты, навели людей на мысль, что этим движением управляют незыблемые законы, а не прихоть и капризы богов и демонов. Сначала существование таких законов стало очевидным только в астрономии (или астрологии, что было практически тем же самым). Явления на Земле происходят настолько сложным образом и подвержены столь многим воздействиям, что древние цивилизации не могли разглядеть сколь-либо отчетливых закономерностей в процессах, управляющих этими явлениями. Однако постепенно новые законы были выявлены и в других областях, кроме астрономии, что привело к идее научного детерминизма: должен быть полный набор законов, которые, учитывая состояние Вселенной в определенное время, описали бы, как она будет развиваться впредь. Эти законы должны действовать везде и всегда, иначе они не будут законами. Не может быть никаких исключений или чудес. Ни боги, ни демоны не могут вмешиваться в ход развития Вселенной.
Во времена, когда принцип научного детерминизма был впервые предложен, единственными известными законами были Ньютоновы законы движения и гравитации. Мы уже говорили о том, как эти законы расширил Эйнштейн в своей общей теории относительности и как были открыты другие законы, управляющие иными аспектами Вселенной.
Законы природы объясняют, как ведет себя Вселенная, но не отвечают на вопрос, который мы задали в начале книги: почему она проявляет себя именно так?
Почему есть что-то вместо того, чтобы не было ничего?
Почему мы существуем?
Почему существует именно этот конкретный набор законов, а не какой-либо другой?
Кто-то может считать, будто ответ на эти вопросы состоит в том, что есть Бог, который решил создать Вселенную именно таким образом. Резонно спросить: кем или чем создана Вселенная, но если ответ — Богом, то возникает другой вопрос: кто создал Бога? При такой точке зрения считается, что есть некая сущность, не нуждающаяся в творце, и ее называют Богом. Подобное мнение известно как основной аргумент в пользу бытия Бога. Однако мы утверждаем, что на эти вопросы можно ответить строго в рамках науки, без привлечения каких-либо сверхъестественных существ.
Согласно идее моделезависимого реализма, описанной в главе 3, наш мозг интерпретирует сигналы, поступающие от органов чувств, путем построения модели внешнего мира. Мы формируем мысленные представления о нашем доме, деревьях, других людях, об электричестве, поступающем из розеток, об атомах, молекулах и других вселенных. Эти мысленные построения и есть единственная реальность, которую мы можем знать. Никакой моделенезависимой проверки реальности нет. Следовательно, хорошо построенная модель создает собственную реальность. Обдумать вопросы реальности и творения нам может помочь пример с игрой «Жизнь», которую в 1970 году придумал молодой кембриджский математик Джон Конвей.
Слово «игра» в данном случае термин, сбивающий с толку. Здесь нет победителей и проигравших, фактически здесь вообще нет игроков. «Жизнь» по сути не игра, а набор законов, управляющих двухмерной вселенной. Это детерминированная вселенная: когда вы установили начальную конфигурацию, или начальное условие, то все, что будет происходить дальше, определяется законами.
Мир, придуманный Конвеем, представляет собой сеть квадратных клеток, похожую на шахматную доску, которая продолжается во все стороны бесконечно. Каждая клетка может быть либо «живой», либо «мертвой» (на иллюстрациях, помещенных далее, они показаны зеленым или черным цветом соответственно). У каждой клетки восемь соседей: сверху, снизу, слева, справа и четыре соседа по диагонали. Время в этом мире не непрерывно, а движется вперед дискретными шагами. Учитывая различное взаиморасположение мертвых и живых клеток, последующие события определяются количеством живых соседей в соответствии с такими законами:
1) Живая клетка с двумя или тремя живыми соседями остается жить (выживание).
2) Мертвая клетка с тремя живыми соседями оживает (рождение).
3) Во всех остальных случаях клетка умирает или остается мертвой. В случае если у живой клетки нет живых соседей или есть только один, она умирает от одиночества; если у нее больше трех живых соседей, она умирает от перенаселенности.
Посмотрим, как же все происходит: исходя из любого начального условия эти законы генерируют поколение за поколением. Изолированная живая клетка или две смежные живые клетки умирают в следующем поколении, потому что у них не хватает соседей.
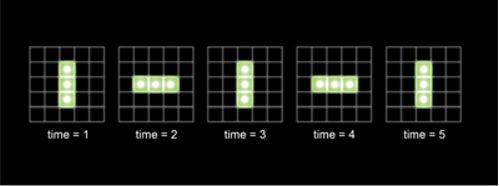
«Мигалки». «Мигалки» — это простой тип составного объекта в игре «Жизнь».
Три живые клетки по диагонали живут чуть дольше. После первого временного шага (этапа) крайние клетки умирают, остается только средняя, которая умирает в следующем поколении. Таким же образом «испаряется» любая диагональная линия клеток. Но если три живые клетки расположены горизонтально в ряд, средняя из них имеет двух соседей и выживает, тогда как две крайние умирают, но в этом случае рождаются клетки, прилегающие к средней сверху и снизу. Таким образом ряд превращается в столбик. Подобным же образом в следующем поколении (то есть на следующем этапе) столбик опять превращается в ряд, и т. д. Такие колеблющиеся фигуры называются «мигалки».
Если три живые клетки расположены в виде буквы Б, события идут по-другому. В следующем поколении клетка, которую огибает Б, получает свое рождение, и возникает фигура, называющаяся «блок» (2x2 клетки). «Блоки» относятся к типу фигур, который называется «натюрморты» или «устойчивые фигуры», потому что они переходят из поколения в поколение не изменяясь. Существует много разных фигур, которые в начальных поколениях изменяются, но вскоре оказываются одним из видов «натюрморта», либо умирают, либо же возвращаются к своему первоначальному виду, а затем процесс повторяется.
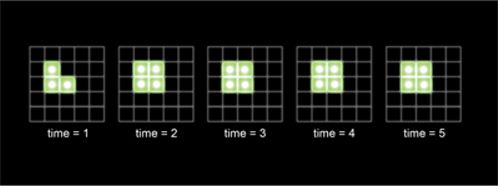
Превращение в «натюрморт». Некоторые составные объекты в игре «Жизнь» развиваются в формы, которым правилами предписано никогда не изменяться.
Существуют также фигуры, называемые «планеры» (или «глайдеры»), которые преобразуются в другие фигуры, а через несколько этапов (временных шагов) возвращаются к своему первоначальному виду, но сместившись на одну клетку вниз по диагонали. Если вы понаблюдаете за таким развитием какое-то время, то увидите, что «планеры» как будто ползут по сетке. Когда они сталкиваются, могут происходить любопытные преобразования, зависящие от формы каждого из «планеров» в момент столкновения.
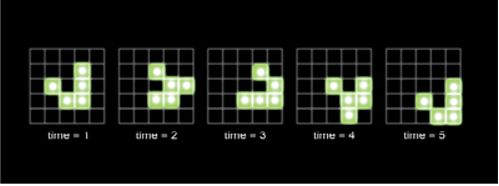
«Планеры». «Планеры» преображаются, принимая промежуточные формы, а потом, сместившись по диагонали, возвращаются к первоначальной форме.
Интересной эту игровую вселенную делает то, что фундаментальная «физика» ее проста, а «химия» может оказаться сложной. Имеется в виду, что составные объекты в ней существуют в различных масштабах. В наименьшем масштабе фундаментальная физика игры говорит нам, что есть лишь живые и мертвые клетки. В более крупном масштабе имеются «планеры», «мигалки», а также «блоки» и другие устойчивые фигуры из группы «натюрмортов». С дальнейшим укрупнением масштаба появляются еще более сложные объекты, такие как «планерные ружья» — стационарные формы, периодически порождающие новые «планеры», которые покидают свое «гнездо» и устремляются вниз по диагонали.
Если некоторое время понаблюдать за игрой «Жизнь» в каком-то одном масштабе, можно распознать законы, управляющие объектами этого масштаба. Например, среди фигур поперечником всего в несколько клеток вы сможете заметить такие законы, как «абсолютно неподвижные „блоки“», «„планеры“, движущиеся по диагонали», а также различные законы для случаев столкновения объектов. Вы можете создать всю физику для любого уровня составных объектов. Эти законы будут описывать сущности и понятия, которые отсутствовали в исходных законах. Там, например, не было таких понятий, как «столкновение» и «перемещение». Начальные законы определяли лишь «жизнь» и «смерть» отдельных неподвижных клеток. В игре «Жизнь», как и в нашей Вселенной, ваша реальность зависит от используемой вами модели.

Начальная конфигурация «планерного ружья». «Планерное ружье» примерно в десять раз больше «планера».
Конвей и его студенты создали этот игровой мир, желая узнать, может ли вселенная, фундаментальные законы которой так же просты, как те, что установлены ими для этой игры, содержать объекты настолько сложные, что они смогут воспроизводить самих себя. Существуют ли в мире игры «Жизнь» такие составные объекты, которые, попросту следуя в течение нескольких поколений (т. е. временных шагов) исходным законам игры, породят другие объекты, подобные себе? Конвей и его студенты не только смогли продемонстрировать, что это возможно, но даже показали, что подобный объект может, в некотором смысле, быть умным! Что мы имеем в виду? Уточним: они показали, что огромные скопления клеток, которые самовоспроизводятся, представляют собой «универсальную машину Тьюринга». В нашем случае это означает, что (для любого расчета, с которым компьютер в нашем физическом мире может в принципе справиться) если на входе задать машине соответствующие данные, то есть снабдить ее условиями игры «Жизнь», то спустя несколько этапов работы машина окажется в том состоянии, когда можно будет увидеть, что получилось на выходе, — это будет соответствовать результатам данного компьютерного расчета.
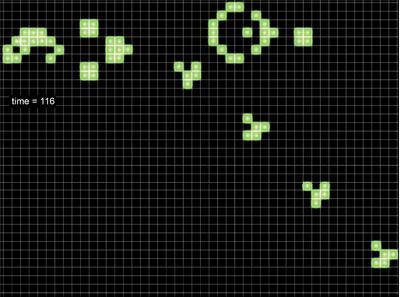
«Планерное ружье» через 116 поколений (этапов). Со временем «планерное ружье» изменяет форму, испускает «планер» и возвращается к своим начальным конфигурации и положению.
Затем оно повторяет процесс бесконечно.
Чтобы почувствовать, как это работает, рассмотрим, что происходит, когда «планеры» наталкиваются на простой «блок» живых клеток размером 2x2. Если «планеры» приближаются подходящим путем, то ранее неподвижный блок сдвинется либо к источнику «планеров», либо от него. Фактически все основные функции современного компьютера, такие как логические вентили И и ИЛИ, также могут быть созданы из «планеров». При таком подходе потоки «планеров» можно использовать для передачи и обработки информации, подобно тому как в физическом компьютере используются электрические сигналы. Как и в нашем мире, такие самовоспроизводящиеся фигуры являются сложными объектами. По одной из оценок, основанной на давней работе венгро-американского математика Джона фон Неймана (1903–1957), минимальный размер самовоспроизводящейся фигуры в игре «Жизнь» — десять триллионов клеток, что примерно равно количеству молекул в одной человеческой клетке.
Живые существа можно рассматривать как сложные системы ограниченного размера, которые стабильны и могут самовоспроизводиться. Описанные выше объекты удовлетворяют условию воспроизводства, но, вероятно, нестабильны: слабое возмущение извне вполне может разрушить чувствительный механизм. Однако легко представить себе, что немного усложненные законы позволят создать и более сложные системы со всеми признаками жизни. Представьте себе существо такого типа, объект в мире, подобном конвеевскому. Такой объект будет реагировать на воздействия окружающей среды и, следовательно, выглядеть принимающим решения. Будет ли такая жизнь знать о своем существовании? Будет ли она обладать самосознанием? Мнения по этому вопросу резко расходятся. Некоторые считают, что осознание своего существования присуще только людям. Это наделяет их свободой воли — способностью делать выбор между различными возможностями действий.
Как определить, обладает ли существо свободой воли? Если мы встретим инопланетянина, как распознать, робот это или существо, обладающее собственным разумом? Поведение робота будет полностью детерминировано, в отличие от разумного существа, обладающего свободой воли. Следовательно, в принципе робота можно будет определить по предсказуемости его действий. Но, как мы уже говорили в главе 2, это может оказаться трудным до невозможности, если существо крупное и сложно устроенное. Мы не можем точно решать даже уравнения для трех и более взаимодействующих друг с другом частиц. А поскольку инопланетянин размером с человека содержал бы около тысячи триллионов триллионов частиц, даже если бы он был роботом, то было бы невозможно решить уравнения и предсказать, что он будет делать. Поэтому мы должны сказать, что любое сложное существо обладает свободой воли, имея в виду, что это есть не его фундаментальное свойство, а лишь признание нашей неспособности произвести расчеты, которые позволили бы нам предсказать его действия.
Пример с конвеевской игрой «Жизнь» показывает, что даже очень простой набор законов может произвести сложные свойства, подобные тем, что присущи разумной жизни. Должно существовать много наборов законов, обладающих этим свойством. Что выбирает законы, управляющие нашей Вселенной? Так же, как и во вселенной Конвея, законы нашей Вселенной определяют развитие системы, учитывая ее состояние в любой момент. В мире Конвея творцами являемся мы — это мы выбираем начальное состояние вселенной, определяя объекты и их расположение в начале игры.
В нашей физической Вселенной аналогами таких объектов игры «Жизнь», как «планеры», выступают отдельные материальные тела. Любой набор законов, описывающих непрерывный мир, подобный нашему, будет иметь понятие энергии, которая сохраняет свое количество, то есть ее количество не изменяется со временем. Энергия пустого пространства будет постоянной, независимой ни от времени, ни от местонахождения. Измеряя энергию любого объема пространства относительно энергии того же объема пустого пространства, эту константу вакуума можно вычесть, поэтому мы вполне можем считать ее равной нулю. Есть условие, которому должны удовлетворять любые законы природы: они должны предписывать, чтобы энергия отдельного тела, окруженного пустым пространством, была положительной, то есть для создания тела нужно проделать работу. Поэтому, если энергия отдельного тела отрицательна, оно может быть создано в состоянии движения таким образом, чтобы его отрицательная энергия была точно уравновешена положительной энергией вследствие его движения. Будь это так, не было бы причины, препятствующей телам возникать где угодно. Пустое пространство было бы тогда нестабильным. Но если для создания отдельного тела нужно потратить энергию, то такой нестабильности не возникает, потому что, как мы уже сказали, энергия вселенной должна оставаться постоянной. Вот что требуется, чтобы вселенная была локально стабильной: нужно сделать ее такой, чтобы ничто не появлялось повсюду просто так из ничего.
Если полная энергия вселенной должна всегда оставаться нулевой и если для создания тела нужно потратить энергию, то как же целая вселенная может быть создана из ничего? Вот зачем нужен закон гравитации. Поскольку гравитация притягивает, гравитационная энергия отрицательна: чтобы разделить связанную гравитацией систему — такую, например, как Земля с Луной, — нужно приложить усилия. Эта отрицательная энергия может быть уравновешена положительной энергией, необходимой для создания материи, но это не так уж просто. Отрицательная гравитационная энергия Земли, например, составляет менее чем одну миллиардную положительной энергии материальных частиц, из которых Земля состоит. Такое тело, как звезда, будет иметь больше отрицательной гравитационной энергии, и чем звезда меньше, чем ближе различные ее части друг к другу, тем больше будет эта отрицательная гравитационная энергия. Но прежде чем она сможет превысить положительную энергию материи, звезда сожмется и превратится в черную дыру, а черные дыры имеют положительную энергию. Вот почему пустое пространство стабильно. Тела, подобные звездам или черным дырам, не могут появиться просто так, из ничего. А вот вселенная целиком может.
Из-за того что пространство и время формируются гравитацией, пространство-время может быть локально стабильным, но глобально нестабильным. В масштабе всей вселенной положительная энергия материи может уравновешиваться отрицательной гравитационной энергией, и потому нет ограничения для возникновения целых вселенных. Поскольку существует гравитация, вселенная может возникнуть самопроизвольно из ничего путем, о котором рассказано в главе 6. Самопроизвольное рождение и есть причина того, что Вселенная существует. Нет необходимости призывать на помощь Бога, чтобы он поджег фитиль и дал начало развитию Вселенной. Именно поэтому есть что-то, вместо того чтобы не было ничего, поэтому существуем и мы.
Почему законы нашей Вселенной таковы, какими мы их описали? Окончательная теория Вселенной должна быть непротиворечива и должна предсказать конечные результаты для тех величин, которые мы можем измерить. Мы увидели, что требуется наличие закона, подобного закону гравитации, а прочитав главу 5, убедились: для того чтобы теория гравитации предсказала конечные величины, она должна обладать так называемой суперсимметрией между фундаментальными взаимодействиями в природе и материей, на которую они действуют. М-теория является общей суперсимметричной теорией гравитации. Поэтому М-теория — единственный кандидат на место полной теории Вселенной. Если же она конечна — а это еще надо доказать, — то она будет моделью вселенной, способной к самопроизвольному возникновению. Мы должны быть частью такой вселенной, поскольку другой непротиворечивой модели нет.
М-теория и есть та единая теория, которую надеялся найти Эйнштейн. То, что мы, люди, сами являясь всего лишь скоплением фундаментальных природных частиц, смогли столь близко подойти к пониманию законов, управляющих нами и нашей Вселенной, представляет собой великую победу. Но, возможно, истинное чудо в том, что абстрактные логические рассуждения привели нас к уникальной теории, предсказывающей и описывающей огромную изумительно разнообразную Вселенную, простирающуюся перед нашим взором. Если теория подтвердится наблюдениями, это станет успешным завершением поисков, длившихся более 3000 лет. Тогда мы разгадаем Высший замысел.
| <<< Назад 7. Кажущееся чудо |
Вперед >>> Словарь терминов |
