Книга: Как работает Вселенная: Введение в современную космологию

1.2.7. Лунные приливы и отливы

1.2.7. Лунные приливы и отливы

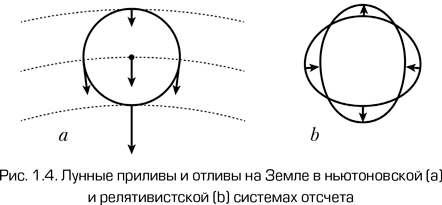
Для объяснения лунных приливов на Земле в рамках ньютоновского подхода мы рассмотрим сначала гравитационное поле неподвижной Луны. Рассматривая ее как точечную массу, мы видим, что силовые линии ее гравитационного поля, т. е. направления ускорения свободного падения на Луну, радиальные. Таким образом, суммарная сила, действующая на любую частицу на Земле, является суммой притяжения к остальной части Земли и силы, действующей в направлении Луны (мы не рассматриваем другие небесные тела, чтобы избежать путаницы). Для перехода к системе отсчета, связанной с Землей, мы должны вычесть ускорение свободного падения в центре масс Земли из ускорения свободного падения, действующего на каждую точку, как показано на рис. 1.4. В результате мы получаем знакомую картину: приливы в направлении к и от Луны и отливы в перпендикулярных направлениях.

Таким образом, с ньютоновской точки зрения приливная сила – это просто разница ускорений свободного падения между произвольной точкой и некоторой опорной точкой, например центром Земли. С релятивистской точки зрения приливная сила – это то, что отличает гравитацию от сил инерции, вызванных, например, ускорением ракеты.

Переходя в систему свободно падающего наблюдателя, вы можете обнулить силу, действующую в одной точке, как правило, в центре масс, но в любой другой точке имеется ненулевая разность – приливная сила. В ОТО приливные силы являются проявлением кривизны пространства-времени.

Вопрос: Почему приливы, вызванные небольшой Луной, сильнее, чем приливы, вызванные огромным Солнцем?

Ответ: Формулу для приливной силы можно найти в учебниках, она утверждает, что эта сила обратно пропорциональна кубу расстояния. Тем не менее, вместо того чтобы просто использовать эту формулу, покажем, как эта зависимость от расстояния может быть получена с помощью простой аналогии.

Рассмотрим два точечных тела единичной массы – одно в центре Земли, а другое на поверхности Земли. Приливная сила во второй точке может зависеть только от трех параметров: от расстояния между двумя точками, в которых находятся тела, от расстояния до Луны, а также от угла между направлением на Луну и линией, соединяющей эти точки. Эта приливная сила, равная разности сил, действующих на две точечные массы, равна также сумме сил, действующих на второе тело и на первое тело, если вторая взята с противоположным знаком.

Воспользуемся электростатической аналогией и заменим эти тела точечными единичными зарядами, а Луну – внешним точечным зарядом, величина которого выбирается таким образом, что силы, действующие на точечные заряды, идентичны гравитационным силам, действующим на точечные массы[20]. Обратим знак центрального заряда (именно поэтому нам понадобилось переключиться на электрическое поле, так как не существует такого понятия, как отрицательная масса). Теперь на заряд в центре Земли действует сила той же величины, но в противоположном направлении. Эти два противоположных заряда образуют диполь, причем его размеры существенно меньше расстояния до Луны.

Сила, с которой точечный заряд, которым мы заменили Луну, взаимодействует с нашим электрическим диполем, равна искомой приливной силе. Согласно третьему закону Ньютона, она равна также силе, с которой диполь действует на точечный заряд в центре Луны. Поле диполя убывает обратно пропорционально кубу расстояния, поэтому поле приливных сил должно убывать по тому же закону. Возвращаясь к гравитации, мы наконец-то получаем, что приливные силы падают обратно пропорционально кубу расстояния до тела, вызывающего приливы, и пропорциональны его массе.

Теперь сделаем некоторые простые расчеты. Солнце весит 2,0?1030 кг и расположено на расстоянии 1,5?108 км. Луна весит 7,3?1022 кг и находится на расстоянии 3,8?105 км. Таким образом, Солнце в 2,7?107 раз тяжелее и в 395 раз дальше, чем Луна. Если возвести отношение расстояний в куб, мы получаем 6,2?107, что в 2,2 раза больше, чем отношение масс. Таким образом, лунные приливы в 2,2 раза сильнее солнечных приливов.

Однако, если нас интересует отношение гравитационных сил, мы должны использовать отношение квадратов расстояний, которое в 176 раз меньше, чем отношение масс, и Солнце легко выигрывает это соревнование. Если мы интересуемся вкладом в гравитационный потенциал, обратно пропорциональный расстоянию, то вклад от галактик в скоплении Девы, расположенных на расстоянии около 54 млн световых лет (св. лет) от Земли, будет существенно большим, чем вклад как Солнца, так и Луны.