Книга: Астрономия на пальцах.

Глава 8. Ансамбль струнных

Глава 8. Ансамбль струнных

Не думаю, что эта заключительная глава будет большой. Но зато она будет очень важной и крышесносной – не столько в смысле сложности, сколько в смысле заключенных в ней идей.

Ученые XIX века жили в правильном механистическом мире. Несколько наивном, но прямом и красивом. Вселенная в их понимании была вечной, бесконечной, предопределенной, а также стационарной. Атомы – неделимыми частицами. Пространство – просто ареной действия, сценой, где происходят события. А время… Что такое время? Сплошная череда перемен!

Физики ХХ века поняли, что все не так просто. Их мир стал динамичным, непредсказуемым и относительным. Вселенная расширялась. Массы, энергии, расстояния и даже темп происходящих событий (время) оказались зависимы от скорости света. Причем, любые сигналы в мире не могли распространяться быстрее этой скорости. Время и пространство физики формально объединили в один пространственно-временной континуум. Атомы перестали быть мельчайшими, потому что на арену знания вышли их детальки – элементарные частицы: электрон, протон и нейтрон. Позже были открыты и другие частицы – нейтрино, антипротоны, позитроны… Причем сами частицы перестали быть «абсолютно твердыми». Нет, не в том смысле, что их можно было разобрать дальше на еще более мелкие детальки. А в том, дорогие мои люди, смысле, что они перестали, во-первых, быть частицами и «размылись», то есть приобрели свойства волн. А во-вторых, при попытках их разбить, разломать они не разваливались на составляющие, а множились, превращаясь в другие частицы. И, грубо говоря, чем больше энергии прикладывалось к ним при столкновении, чтобы разломать, тем больше частиц образовывалось. Потому что энергия, оказывается, может превращаться в массу и наоборот!

Чтобы глубже понять устройство огромной Вселенной, ученые бились с загадками самых малых ее деталек – элементарных частиц, полей, вакуума. Им хотелось написать Теорию всего. А для этого требовалось объединить все известные физикам взаимодействия в единое целое и понять, как это все работает.

Не давали физикам также вопросы: а что стоит за материей?.. что такое электрический заряд?.. что такое масса?.. и почему все именно так, а не иначе?

И вот в попытках ответов они придумали так называемую теорию струн – она теперь главнейший кандидат на Теорию всего.

Оказалось (с точки зрения теории струн), что в основе материи лежат некие струны – крохотулечные линейные объекты, которые могут колебаться, как струны. И по расчетам выходило, что разные колебания этих струн воспринимаются нами в нашем мире как разные свойства элементарных частиц – заряд, масса…

Мир сделан из микровибраций!

Теория оказалась весьма интересной, крайне запутанной и очень перспективной. А также мало кем понимаемой. Но нам с вами важно понять в этой теории самое главное: эти самые струны, из которых все сделано, ни из чего не состоят!

Когда мы говорим, что нечто состоит из чего-то, мы, используя бытовой опыт, имеем в виду какое-то вещество. Но со струнами ситуация уже иная! Струны как раз и были придуманы для того, чтобы ответить на вопрос, из чего сделано вещество, то есть элементарные частицы. И вот выяснилось (с точки зрения данной теории), что из неких струн. Они первичны.

– Ну хорошо! – Воскликнет пораженный в самое сердце и не желающий сдаваться читатель. – А струны-то эти все же из чего сделаны, раз они существуют? Из чего они, черт побери?!

Отвечу: из чистой математики!

Дело в том, что проверить справедливость теории струн практически нельзя. Для этого потребуются столь сумасшедшие энергии, каких мы в наших земных ускорителях не достигли и вряд ли когда-нибудь достигнем. Такие энергии были лишь в первые секунды существования Вселенной. По сути, человечество вплотную приблизилось к моменту, когда чистая математика пришла на смену физике. Точнее, математическая геометрия. Физика в пределе свелась к геометрии пространства.

Вообще, первым, кто свел физику к геометрии был Эйнштейн. В его теории относительности гравитация, то есть всемирное тяготение – это всего лишь следствие искривления пространства. Тяжелые тела искривляют вокруг себя пространство и, грубо говоря, по этим вдавленностям «сцены» они и скатываются друг к другу – как бы притягиваются. Или не «как бы», потому что реально притягиваются – именно так мы это и воспринимаем.

И вот теперь оказалось, что не только гравитация, но и все прочие физические проявления – лишь следствие геометрии нашего многомерного мира.

Стоп! А что значит «многомерный мир»? И что это все-таки за струны такие геометрические в удивительной теории струн? Отвечу…

Мы не можем сказать, из чего «сделаны» струны, сам вопрос не имеет смысла. Но мы можем описать эти струны, понять, какие они.

Они – одномерные. А пространство, в котором они колеблются, – многомерное.

Непонятно?

Сейчас разберемся. Что такое мерность пространства? Ну, это все знают! А кто не знает, сейчас узнает.

Наше пространство трехмерно. В нем три измерения – длина, ширина и высота. Вы спросите: а как еще может быть? Ну, в теории может быть по-разному. Школьная геометрия, например, изучает, в основном, двумерное пространство. Двумерное пространство – это плоскость. На плоскости есть только два измерения – длина и ширина, высоты нету… Одномерное пространство – линия. В нем только одно измерение – длина… И есть нуль-мерное пространство – точка. Точка – она и есть точка – ни длины в ней, ни ширины, ни высоты…

Можно представить себе некий двумерный мир и живущих в нем плоскатиков, причем ясно, что жизнь у ребят не сахар: им приходится производить выделения из организма через то же самое отверстие, через которое они едят. То есть какают плоскатики через рот. Иначе невозможно: если вы попробуете нарисовать плоскатика в виде «плоской трубы», в один конец которой входит пища (рот), а из другого конца выходит бяка (попа), вы увидите, что ваш плоскатик развалился на две не соединенные друг с другом части. Человеку в этом смысле повезло: в трехмерном мире благодаря высоте тело не разваливается на две части.

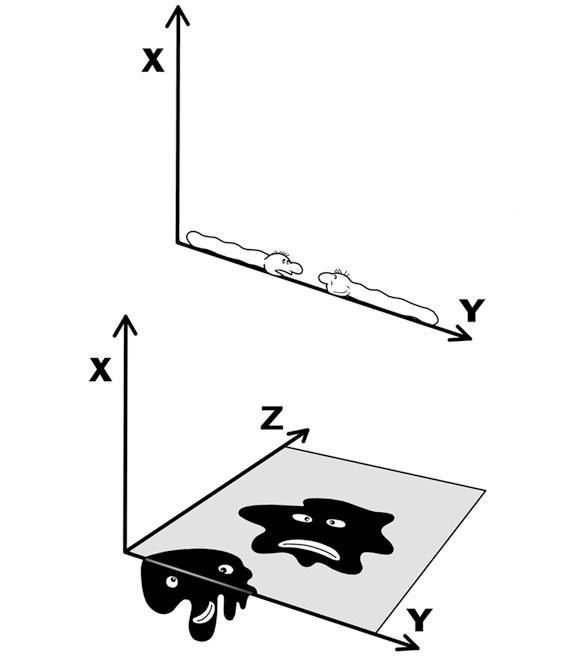
Плохо быть плоскатиком! И линейщиком… Для удобства восприятия у линейных созданий показана некая толщина, чтобы мы их увидели. Но вообще-то поперечного размера не должно быть в одномерном мире.

В одномерном мире ситуация еще хуже – живущие там линейщики не смогли бы даже обойти друг друга, каждый житель этого мира может иметь только двух соседей – одного слева и одного справа.

Пространственное измерение – это перпендикуляр, который можно восстановить к другому измерению. Если к одномерной линии прочертить под углом 90 градусов другую линию (перпендикуляр), получится уже двумерность, то есть плоскость. В плоскость тоже можно воткнуть сверху перпендикуляр – третью координату – получится пространство. В плоскости существуют только плоские фигуры – треугольники, окружности, квадраты… А в пространстве объемные – пирамиды, шары, кубы, конусы… Это все легко себе представить, не так ли?

А вот четырехмерное пространство представить себе никак невозможно – просто потому, что мы не можем выйти за пределы своего трехмерия и воткнуть еще один перпендикуляр так, чтобы он располагался под прямым углом к остальным трем. Некуда его втыкать в нашем мире! Но это не значит, что четырехмерие, пятимерие и так далее не могут существовать.

Могут.

Теоретически. И поэтому в теории струн одномерные, не имеющие толщины струны колеблются в 10-мерном пространстве. Наш мир, получается, десятимерен, если верить теории струн! Почему же мы не видим других измерений, а видим только три? Да потому что остальные измерения свернуты, отвечает теория, они компактифицированы. «Лишние» измерения скручены в такие как бы трубочки, диаметр коих столь мал, что нами не замечается.

Увы, наглядных представлений тут нет. Потому понять это все можно только с помощью математики, оперируя сложными формулами, которые понимают считаные сотни людей на планете. И тут возникает главный вопрос: ну ладно, а почему вообще математика, то есть чистой воды голая придумка человека, правильно описывает реальный мир? Почему мир математичен, то есть подчиняется неким правилам математики, высосанным из пальца? Ведь, повторюсь, математика – это целиком выдуманная наука, состоящая из абстрактных значков. Значки эти и правила, по которым ми можно оперировать, придуманы людьми.

Отчего же природа им подчиняется?

Это величайшая загадка мироздания. Объяснения нет. Но математические и геометрические закономерности (в виде так называемых золотых сечений, например) мы видим везде в природе. Пока что, в какие бы глубины вселенной и микромира мы ни забрались, всюду математика работает. И нет никаких причин полагать, что когда-нибудь она откажет, будучи не в силах описать мир. Более того, среди строгих ученых ходит поговорка о том, что любая наука является наукой лишь настолько, насколько она оперирует математикой. С этой точки зрения история – не наука, литературоведение – не наука, психология – не наука. Ибо нету в них нужной для науки точности, которую привносит в дисциплину математика! Но почему работает сама математика, будучи голой придуманной абстракцией, никто не знает.

Ответа на сей вопрос пока нет. И то, что физика на каких-то самых глубоких уровнях миропознания свелась к геометрии пространства и чистой математике, поражает. Но с другой стороны, а разве могло быть иначе?..