Книга: Эволюция и прогресс

Глава 3. Факторы микроэволюции

Глава 3. Факторы микроэволюции

Для того чтобы в вопросах эволюции оставаться на твердой почве фактов, разумно руководствоваться принципом униформизма (актуализма), т. е. при объяснении явлений отдаленного прошлого исходить из анализа процессов, совершающихся в настоящее время. Не будем спешить и придумывать особые законы, влекущие эволюцию организмов по пути морфофизиологического прогресса. Сначала постараемся понять протекающую перед нашими глазами жизнь природных популяций, после чего сделаем попытку распространить эти (микроэволюционные) процессы на гораздо большие отрезки времени.

Генный поток

Сначала попробуем ответить на вопрос: что такое вид? Это понятие относится к наиболее важным и сложным в современной биологии. Начнем с того, что особи, связанные отношением родства, принадлежат одному виду. Под родством же люди обычно подразумевают каким-то образом зарегистрированную общность происхождения. Например, братья и сестры имеют общими двух предков в поколении родителей. Двоюродные братья и сестры имеют общих предков в поколении дедов, троюродные — в поколении прадедов и т. д. Таким образом, с понижением степени родства общие предки перемещаются на все более отдаленные поколения. Совокупность особей, связанную отношением родства (включая и самые отдаленные его степени), можно было бы назвать видом. По существу, это очень близко к библейскому определению рода человеческого как всех потомков Адама и Евы. Однако такое определение крайне неудобно и ненадежно. Разве особи разных видов (например, волки и лисицы) не связаны отдаленным (эволюционным) родством? Как определить ту степень родства, которая еще позволяет отнести организмы к одному виду?

С генетической точки зрения, от предка к потомку передаются практически в неизменном виде наследственные факторы, гены. Поэтому общность происхождения — это общность генов. Миф об Адаме и Еве на самом деле довольно точно отражает реальную ситуацию, во всяком случае, есть веские основания считать, что вся совокупность наследственных факторов человечества восходит к генам очень небольшой группы особей. И если бы гены при передаче от родителей к потомкам не изменялись (т. е. не мутировали), то все люди были бы действительно братьями.

В ядре любой соматической (т. е. не половой) клетки организма имеются два аллельных варианта каждого гена, два аллеля — один от матери, другой от отца. Исключение составляют только половые клетки — гаметы, в их геноме каждый локус представлен всего одним аллелем, такой набор генов называется гаплоидным. При оплодотворении гаплоидные геномы гамет соединяются в диплоидный геном зиготы, который затем точно копируется механизмом клеточного деления. Таким образом, геномы всех соматических клеток организма на всех стадиях его развития (включая и зиготу) идентичны. Гаплоидный геном гамет возникает в результате действия особого клеточного механизма — мейоза. Суть его состоит в том, что в одну гамету попадает только один аллельный вариант каждого генного локуса, какой именно — материнский или отцовский — решает случай.

Сделаем одно важное (и в какой-то степени спорное) предположение. Будем считать, что все особи одного вида обладают набором одних и тех же генных локусов, т. е. при мутировании может изменяться не число, а только аллельное состояние локусов. Потерю гена формально можно трактовать как его мутирование к нулевому аллелю. Правда, с добавлением гена (его дупликацией) вопрос обстоит сложнее. Итак, примем, что все особи одного вида содержат в хромосомах каждой клетки (в своем геноме) одно и то же число генных локусов, или генов.

Поскольку при передаче наследственного материала от родителя к потомку с некоторой вероятностью может произойти мутация по любому гену, то чем ниже степень родства особей, тем выше вероятность различия аллелей по каждому локусу. Различие аллелей ведет к различию фенотипов, т. е. к уменьшению внешнего сходства. Следовательно, степень родства можно оценить по близости внешнего вида особей. Мы оцениваем такое сходство на глаз, интуитивно схватывая огромное число признаков. В итоге, глядя на окружающие нас живые организмы, мы можем рассортировать их по внешнему виду, что, как правило, эквивалентно разбиению по видовой принадлежности.

Нет ли способа объективно оценивать степень сходства генов? Оказывается, такой способ есть, и им уже давно пользуются биологи. Считается, что особи разного пола принадлежат к одному виду, если они способны к самостоятельному скрещиванию и их потомство плодовито. При оплодотворении две гаметы родителей сливаются в зиготу, при этом объединяются два набора аллелей — от отца и матери. Под контролем конкретной комбинации аллелей (генотипа) зигота превращается во взрослый организм. В связи с этим можно говорить о генетической программе развития организма, хотя это выражение не более, чем метафора, во всяком случае данная «программа» не имеет ничего общего с компьютерной. Итак, онтогенез потомка протекает под контролем сразу двух генетических программ. Если они не очень хорошо согласованы, то онтогенез может либо вовсе не завершиться, либо привести к созданию дефектной особи. Таким образом, метод скрещивания фактически оценивает близость аллелей по локусам, контролирующим онтогенез. Именно этим методом и пользуются особи одного вида в своей естественной жизни. Впрочем, для многих животных со сложным поведением оценка видовой принадлежности по внешним признакам также является необходимым условием для скрещивания, и спаривания не произойдет, если особи разных полов не «поймут» ритуала ухаживания.

Ситуация, когда любые две взрослые разнополые особи одного вида могут стать участниками скрещивания, называется панмиксией. Естественно, в реальности условия для панмиксии выполняются далеко не всегда, поскольку для соединения любой пары гамет нужно, Чтобы родители — обладатели гамет — находились недалеко друг от друга. Тем не менее в пределах этого «недалеко» панмиксия выполняется. Например, жителей большого этнически однородного города с хорошо организованным транспортом можно считать связанными панмиксией.

У большинства зоологических видов особи способны к активному движению, кроме того, могут двигаться их личинки или гаметы. У ботанических видов к широкому расселению способны семена, споры, пыльца, а нередко и фрагменты растений. Мы можем взглянуть на это явление немного иначе и увидеть в нем блуждание генов по ареалу вида. Данный процесс имеет много общего с диффузией броуновских частиц. Поток таких частиц в каком-то направлении пропорционален градиенту (перепаду) их концентрации вдоль этого направления и коэффициенту диффузии — параметру, отражающему подвижность самих частиц. В конечном счете концентрация частиц во всей области их блуждания выравнивается, и наступает диффузионное равновесие.

Точно так же по ареалу вида «движутся» и аллели. Как и в случае диффузии, через некоторое время, определяемое размерами ареала вида и способностью генов к перемещению, должно установиться равновесие аллельных частот. Если скорость движения генов высока, то процесс выравнивания этих частот идет быстро. При панмиксии, когда в скрещивание может вступить любая пара разнополых особей, аллельное равновесие устанавливается практически моментально, т. е. за одно поколение. Нередко мы имеем дело только с переходом к такому равновесию, когда на территории, занятой видом, обнаруживаются градиенты по частотам разных аллелей. Эти градиенты — клины — можно изобразить графически в виде семейства изолиний, как это принято для топографических карт. Вдоль такой изолинии частота аллеля постоянна. Где изолинии гуще, градиент частоты аллеля круче.

По аналогии с диффузионным потоком можно ввести понятие о генном потоке как о переносе аллелей через единицу длины изолинии. Ясно, что такой поток будет тем мощнее, чем круче градиент и чем больше коэффициент диффузии генов. Наиболее мощные генные потоки образуются, когда в какую-то область ареала с высокой концентрацией определенного аллеля проникает группа иммигрантов с другой частотой того же аллеля.

Представим себе, что область блуждания броуновских частиц разделена на несколько отсеков перегородками с разной проницаемостью. Понятно, что если все частицы поместить в один из таких отсеков, то характер последующей диффузии будет существенно зависеть от геометрии расположения перегородок и проницаемости каждой из них. Точно так же территория, где обитают особи одного вида, далека от однородности. Здесь могут быть и реки, и горы, и луга, и леса, — и все это создает препятствия (барьеры) для генных потоков.

Ясно, что если вид занимает сильно пересеченную местность, то время выравнивания концентраций аллелей будет много больше, чем в случае однородного ландшафта. Более того, в реальной ситуации существует немало районов, отделенных от остальных частей ареала практически непроницаемыми барьерами. Представим ареал как замкнутое пространство, разделенное на ячейки барьерами разной проницаемости. Внутри таких ячеек препятствий для генного потока практически нет, поэтому аллельные частоты в них выравниваются сравнительно быстро. Во всяком случае, скорость этого процесса внутри ячеек на несколько порядков выше, чем на их границе. Ясно, что даже в соседних ячейках частоты одних и тех же аллелей могут резко различаться. Вот эту-то часть вида, населяющую одну ячейку, и назовем популяцией. Каждая популяция может быть охарактеризована своим генофондом, т. е. составом аллелей каждого локуса. Популяцию, занимающую ячейку с непроницаемыми стенками, назовем изолированной.

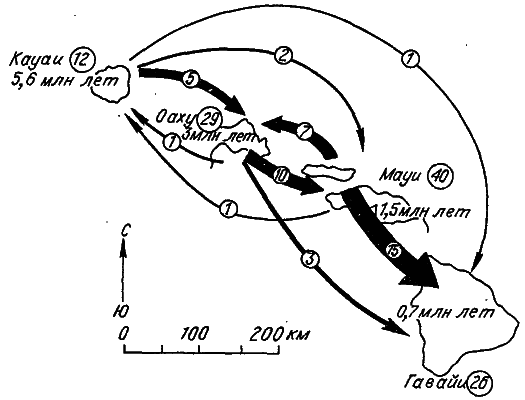
Рис. 9. Схема видообразования гавайских дрозофилид (по: [Carson, 1983]).

Стрелками показаны направление и число заносов мух-основательниц новых видов. В кружках — количество видов-эндемиков каждого острова.

Встает естественный вопрос, как особи попадают в изолированные ячейки? Можно лишь заметить, что абсолютно непроницаемых барьеров нет, кроме того, их проницаемость со временем изменяется. Если виды существуют в течение миллионов лет, то легко себе представить, что большинство барьеров в их ареалах изменяют за это время свою проницаемость в широчайшем диапазоне. Даже такой молодой вид, как Н. sapiens (его возраст оценивают всего в 40 тысяч лет), уже успел столкнуться с неоднократным наступлением и отступлением ледника, представляющего собой весьма эффективный изолирующий барьер.

Американский генетик Х. Карсон сумел восстановить родословную одной группы дрозофилид, обитающих на Гавайских островах (рис. 9). Эти вулканические острова возникали друг за другом в направлении с северо-запада на юго-восток. Самому древнему острову Кауаи 5,6 миллиона лет, а самому молодому острову Гавайи — всего 700 тысяч лет. Анализ политенных хромосом 97 видов гавайских дрозофил привел Карсона к заключению, что все они происходят от одного вида, обитавшего на острове Кауаи. Затем мухи проникли на более юный остров Оаху и, наконец, на остров Гавайи. Число родственных видов во много раз превосходит число островов, поэтому следует предположить, что иногда происходило попадание мух с одного заселенного острова на другой. При этом, несмотря на общность происхождения, иммигранты не скрещивались с туземцами, т. е. обе группы дрозофилид за время географического разобщения успевали стать разными видами. Залеты мух с острова на остров относятся к очень редким событиям, поэтому скорее всего в основе каждого нового вида стояла всего одна осемененная самка.

Этот пример показывает, что для интеграции генофондов популяций в единый генофонд вида продолжительность существования барьеров должна быть намного меньше времени превращения изолированной популяции в новый вид. Очевидно, что со временем в разделенных друг от друга частях некогда единой популяции могут произойти изменения аллельного состава генов, достаточные для того, чтобы воспрепятствовать спариванию особей или нарушить нормальное течение онтогенеза их потомков; иными словами, разобщенные генофонды станут несовместимыми. Такая несовместимость представляет собой особый, самый эффективный, генетический барьер, разделяющий популяции навсегда.

Итак, на популяции одного вида постоянно действуют два фактора, противоположных по своему конечному эффекту. Генный поток стремится слить генофонды популяций в единый генофонд, тогда как процесс видообразования пытается воздвигнуть между временно разобщенными популяциями непреодолимые генетические барьеры. Далее нам предстоит понять, какие факторы лежат в основе генетической дифференциации популяций.

Элементарный акт микроэволюции

Очевидно, что в ходе эволюции идет замещение одних аллелей на другие в ряде локусов. Будем считать элементарным микроэволюционным актом замещение в одном из локусов старого аллеля на новый у всех особей популяции. Учитывая огромные численности природных популяций (10⁵ — 10⁹ особей), «элементарный акт» микроэволюции требует для своего завершения длительного времени. В связи с этим вспомним некоторые рассмотренные выше эволюционные теории.

С точки зрения приверженцев номогенеза, эволюционный сдвиг развивается под влиянием каких-то внутренних факторов без всякой связи с изменениями окружающей среды. По мнению Л.С. Берга, «при возникновении новых географических форм (видов, подвидов, наций) образованием новых признаков захватывается громадная масса особей, обитающих в определенной географической местности». Такое явление можно было бы объяснить, допустив строгую направленность характера мутирования, когда у большинства особей популяции в клетках зародышевого пути в значительной части локусов происходит превращение старых аллелей во вполне конкретные новые. Фантастичность такого представления самоочевидна.

С точки зрения ламаркизма, процесс возникновения новых аллелей уже с самого начала имеет приспособительное значение. Иными словами, между изменениями среды и характером мутирования должна существовать связь, обусловленная каким-то неизвестным молекулярным механизмом. Главное состоит в том, что возникшие мутанты должны быть лучше приспособлены к окружающей среде. Скажем, если в среде обитания популяции падает концентрация кислорода, то в локусах, кодирующих полипептиды гемоглобина, возникают мутации, повышающие сродство этого белка к кислороду. Если же затем в окружающей среде концентрация кислорода вновь повышается, то локусы гемоглобина мутируют в обратном направлении. Заметим, что эти мутации должны происходить в клетках зародышевого пути, в которых гены гемоглобина даже не экспрессируются. Все наши знания о характере мутирования не соответствуют такому ходу событий.

Наиболее спокойной, целиком основанной на известных фактах, представляется нам точка зрения неодарвинизма (вейсманизма). Новые аллели в данном случае возникают совершенно спонтанно: ни скорость возникновения мутаций, ни их эффект никак не связаны с изменениями окружающей среды. При этом каждый локус можно охарактеризовать особым свойством— мутабильностью, т. е. вероятностью смены им аллельного состояния. Для ряда генов, изменения которых ведут к четким, легко регистрируемым изменениям фенотипа особей, мутабильность была измерена. Для совершенно разных организмов она составила 10^-5—10^-6 на одну копию локуса за генерацию. Иными словами, из каждых 100 тысяч особей, возникших в популяции за поколение, лишь одна может оказаться носителем новой мутации по конкретному гену.

Заметим, что для завершения элементарного микроэволюционного акта мутантный аллель должен заменить старые аллели во всех экземплярах этого локуса в популяции. Расчеты показывают, что надеяться исключительно на процесс мутирования по меньшей мере неразумно. Даже при строгой направленности перехода A₁ ? А₂ (где А₂ — новый аллель, а А₁ — старый) для превращения только половины старых аллелей в новые при мутабильности 10^-5 надо ждать около 70 тысяч поколений. К тому же старый аллель может превратиться в совсем другие аллели — А₃, А₄и т. д., и их эффект на фенотип совсем не обязан совпадать с эффектом аллеля А₂. Если представить, например, что доля новых аллелей, изменяющих фенотип особи в одном направлении, равна доле аллелей с противоположным эффектом, то средний фенотип особи популяции вообще останется неизменным, лишь постепенно будет возрастать многообразие аллелей, а следовательно, и многообразие фенотипов. Итак, с неодарвинистской точки зрения, элементарный микроэволюционный акт не может быть обеспечен одним мутированием, для этого нужны дополнительные факторы.

Естественный отбор в популяциях

Мы уже упоминали о том, что Ч. Дарвин ввел понятие естественного (природного) отбора по аналогии с отбором искусственным. Последний сознательно или бессознательно осуществляется человеком, который отбирает на потомство особей с «полезными» для него свойствами. При естественном отборе в качестве селекционера выступает сама природа. Но сказать «природа», значит, не сказать ничего, с равным успехом можно было бы употребить и слово «бог». Какие же реальные факторы стоят за словами «естественный отбор»? Сам Дарвин трактует это понятие следующим образом: «Я назвал это начало, в силу которого каждое незначительное изменение, если оно полезно, сохраняется, естественным отбором…» Иными словами, природа находит «полезным» любое наследуемое свойство особей, которое повышает их жизнеспособность, т. е. их шансы на выживание в борьбе за жизнь.

Попробуем подойти к этому немного строже. Определим жизнеспособность как вероятность особи завершить свой онтогенез. Раз дарвиновская «полезность» наследуется, значит, можно найти гены, чьи аллели обеспечивают своих носителей разной жизнеспособностью. В популяционной генетике каждому генотипу приписывается его приспособленность — величина, которая показывает, каковы у обладателей данного генотипа шансы на вклад своих аллелей в генофонд взрослых потомков. Легко заметить, что понятие «приспособленность» шире, чем «жизнеспособность». Ведь особи с равной выживаемостью могут различаться по числу производимых гамет, шансам найти партнера по спариванию, оплодотворяющей способности гамет и т. д. Очевидно, что все такие наследуемые свойства дают их носителям больше шансов передать свои гены потомкам. В связи с этим выделяют несколько компонент приспособленности — жизнеспособность, плодовитость, скорость индивидуального развития и др.

В рассматриваемой ниже простейшей модели отбора приспособленность отождествляется только с одной из ее главных компонент — жизнеспособностью. Пусть в популяции, насчитывающей N особей, локус А представлен всего двумя аллелями А₁ и А₂. Тогда особи должны разделиться на три генотипических класса: 1) гомозиготы А₁А₁ с численностью N₁₁; 2) гомозиготы А₂А₂ с численностью N₂₂; 3) гетерозиготы А₁А₂ с численностью N₁₂, т. е.

N = N₁₁ + N₂₂ + N₁₂. (3.1)

Каждая особь вносит в генофонд популяции два экземпляра гена А, или (выражаясь несколько иначе) каждая особь является донором (или поставщиком) двух экземпляров этого локуса. Гомозиготы А₁А₁ вносят 2N₁₁ копий аллеля А₁, гомозиготы А₂А₂— 2N₂₂ копий аллеля А₂, тогда как гетерозиготы А₁А₂— 2N₁₂ копий аллеля А₁ и столько же копий аллеля А₂. Отсюда легко оценить долю (частоту) каждого аллеля среди всех 2N экземпляров локуса А, которыми располагает генофонд популяции. Обозначим частоту аллеля А₁ через р, а частоту аллеля А₂ через q (отметим, что р + q = 1). Эти частоты можно вычислить по формулам

p = (2N₁₁ + N₁₂) / 2N = (N₁₁ + 0,5N₁₂) / N, (3.2)

q = (2N₂₂ + N₁₂) / 2N = (N₂₂ + 0,5N₁₂) / N. (3.3)

Гетерозиготы являются донорами сразу двух аллелей, в связи с этим (чисто формально) можно считать, что одна половина гетерозигот вносит в генофонд аллель А₁, а другая — аллель А₂. Тогда всех особей популяции можно представить в виде суммы двух классов — доноров аллеля А₁ с численностью N₁ и доноров аллеля А₂ с численностью N₂. При этом

N₁ = N₁₁ + 0,5N₁₂, (3.4)

N₂ = N₂₂ + 0,5N₁₂. (3.5)

Взглянув на правые части равенств (3.2) и (3.3), мы видим, что в популяции частота каждого аллеля равна доле его доноров:

p = N₁ / N; q = N₂ / N. (3.6)

Рассмотрим популяцию на двух стадиях развития ее особей — на стадии зиготы и взрослого организма. Обозначим численность зигот через N, а численность взрослых — через N'. Каждая из этих величин (N и N') складывается из численностей трех генотипических классов: N₁₁, N₂₂, N₁₂ — для зигот и N₁₁', N₂₂', N₁₂' — для взрослых. Теперь каждому генотипическому классу припишем его приспособленность: w₁₁ — гомозиготам A₁A₁, w₂₂ — гомозиготам А₂А₂ и w₁₂— гетерозиготам. Определим приспособленность каждого генотипа как долю зигот (с данным генотипом), достигших взрослой стадии, т. е.

w₁₁ = N'₁₁ / N₁₁; w₁₂ = N'₁₂ / N₁₂; w₂₂ = N'₂₂ / N₂₂. (3.7)

Так же можно ввести представление и о приспособленности любой группы генотипов. Например, можно говорить о средней приспособленности популяции (w) как о доле всех зигот, успешно завершивших развитие. Аналогично определяется средняя приспособленность доноров каждого аллеля — w₁ и w₂:

w = N' / N; w₁ = N₁' / N₁; w₂ = N₂'/ N₂. (3.8)

Наша главная задача состоит в том, чтобы определить, как под действием отбора изменяется аллельный состав популяции, иначе говоря, как изменяется частота аллелей А₁ и А₂ за время онтогенеза особей.

Доля аллеля в генофонде популяции равна доле его доноров (формулы (3.6)). В случае аллеля А₂ это (N₂ / N) — на стадии зигот и (N₂' / N') — на стадии взрослых. Поэтому сдвиг частоты аллеля А₂ в результате отбора (?q) можно получить как разность: (N₂' / N') — (N₂ / N). Выразив численности взрослых через численности зигот (см. уравнения (3.8)), получим

?q = N₂*w₂ / Nw — N₂ / N = q((w₂ — w) / w). (3.9)

Итак, сдвиг частоты аллеля в генофонде популяции в результате отбора равен частоте этого аллеля до отбора, умноженной на относительное превосходство приспособленности его доноров над средней приспособленностью популяции.

Отбор в панмиктической популяции

Перейдем к панмиктической популяции. Здесь при оплодотворении аллели гамет соединяются в генотипы зигот по правилам свободного попарного комбинирования. Зиготы с генотипами А₁А₁, А₁А₂ и возникают в соотношениях р²: 2pq: q² (рис. 10). Эти же соотношения, получившие название закона Харди-Вайнберга, будут справедливы и для взрослых членов популяции, если приспособленность всех генотипов одна и та же. Закон Харди-Вайнберга довольно часто выполняется в природных популяциях, он позволяет легко вычислять частоты генотипов, исходя из частот аллелей.

В нашей модели отличия в приспособленности особей обусловлены только разным уровнем их жизнеспособности, поэтому численности зигот трех генотипических классов А₁А₁, А₁А₂ и А₂А₂ соответственно равны Np², 2Npq и Nq². Тем самым зиготы в точности отражают генофонд популяции взрослых особей предыдущего поколения. В результате действия отбора численности генотипов взрослых особей, развившихся из зигот, приобретают вид

N₁₁' = Np²w₁₁; N₁₂' = 2Npqw₁₂; N₂₂' = Nq²w₂₂. (3.10)

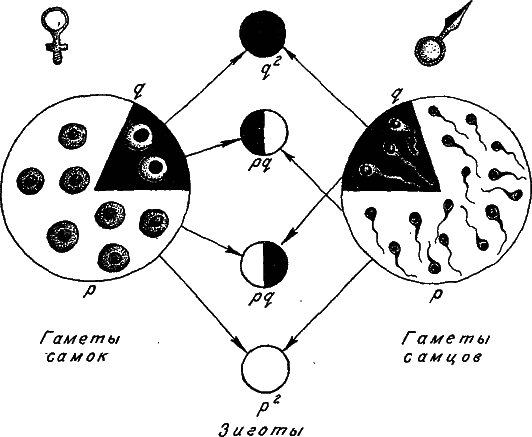
Рис. 10. Схема формирования генотипов зигот при случайном соединении гамет (при панмиксии).

Объяснения в тексте.

Численность всех взрослых особей после отбора связана с численностью зигот уравнением

N' = N(р²w₁₁ + 2pqw₁₂ + q²w₂₂). (3.11)

Поскольку отношение N'/N выражает среднюю приспособленность популяции (см. уравнения (3.8)), поделив обе части уравнения (3.11) на N, получим

w = р²w₁₁ + 2pqw₁₂ + q²w₂₂. (3.12)

По аналогии с формулой (3.5) можно получить численность доноров аллеля А₂ после отбора, т. е. среди взрослых потомков

N₂' = N₂₂' + 0,5N₁₂', (3.13)

или, учитывая соотношения (3.10),

N₂' = Nq²w₂₂ + Npqw₁₂. (3.14)

Поделив обе части этого уравнения на N₂ = Nq (см. (3.6)), получим значение приспособленности доноров аллеля А₂:

w₂ = N₂' / N₂ = (Nq(qw₂₂ + pw₁₂)) / Nq, (3.15)

т. е.

w₂ = pw₂₂ + qw₁₂.

Точно так же можно показать, что

w₁ = pw₁₁ + qw₁₂. (3.16)

Итак, мы располагаем всеми данными для вычисления сдвига частот аллелей после отбора (см. уравнение (3.9)).

Отбор в смысле Ч. Дарвина основан не на абсолютном уровне истребления молодых особей, а на различиях в степени такого истребления. В связи с этим приспособленность какой-то группы особей удобно объявить равной единице, а приспособленность других групп представить в виде суммы 1 + s (s — коэффициент отбора). Такой прием позволяет рассмотреть наиболее интересную для нас задачу — судьбу мутаций, влияющих на относительную приспособленность их носителей.

Судьба вредной мутации

Предположим, что в огромной панмиктической популяции возник и каким-то образом распространился новый аллель А₂ локуса А. (Ранее этот локус был представлен аллелем А₁.) Ясно, что мутантный аллель может встречаться в гомо- и гетерозиготном состояниях. Если мутация вредная, значит, приспособленность гомозигот А₂А₂ должна быть ниже, чем у гомозигот по нормальному аллелю А₁А₁. Это обстоятельство мы можем отразить равенствами w₁₁ = 1, w₂₂ = 1—s. Возникает вопрос: какая приспособленность будет у гетерозигот А₁А₂?

В классической генетике рассматриваются три случая: 1) мутация рецессивна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по нормальному аллелю w₁₂ = w₁₁ = 1; 2) мутация доминантна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по мутантному аллелю w₂₂ = w₁₂ = 1—s; 3) случай неполного доминирования, когда приспособленность гетерозигот ниже, чем у гомозигот по нормальному аллелю, но выше, чем у гомозигот по мутантному. Степень доминирования можно оценить с помощью специальной величины А, варьирующей от нуля до единицы. При этом приспособленность гетерозигот можно выразить формулой w₁₂ = 1 — hs, охватывающей все три рассмотренных выше случая. При h = 0 мы имеем дело с рецессивной вредной мутацией, при h = 1 — с доминантной, а при неполном доминировании — 0 < h < 1.

Особый интерес для нас представляет случай полудоминирования, когда h = 0,5. Дело в том, что, по-видимому, большинство вредных мутаций, постоянно возникающих в природных популяциях, полудоминантны. Приспособленности генотипов в этом случае определяются соотношениями

w₁₁ = 1; w₂₂ = 1 — s; w₁₂ = 1 — 0,5s. (3.17)

Эти равенства позволяют вычислять (с помощью формулы (3.12)) значение средней приспособленности популяции:

w = р² + 2pq(1 — 0,5s) + q²(1 — s),

или

w = (р² + 2pq + q²) — qs(р + q).

Напомним, что p + q = 1, поэтому

w = 1 — qs. (3.18)

Аналогично с помощью уравнения (3.15) можно оценить приспособленность доноров мутантного аллеля:

w₂ = q(1 — s) + р(1 — 0,5s) = 1 — qs — 0,5ps. (3.19)

Теперь, подставив в уравнение (3.9) только что полученные значения для w и w₂, получим сдвиг в частоте мутантного аллеля за одно поколение отбора:

?q = -0,5(pqs / 1 — qs). (3.20)

Так как мутация возникла недавно, то ее частота должна быть очень низкой. Если к тому же невелик и коэффициент отбора, то знаменатель правой части уравнения (3.20) мало отличается от единицы. Поэтому сдвиг частоты мутантного аллеля за одно поколение отбора можно оценить с помощью приближенной формулы

?q ? -0,5pqs. (3.21)

Знак минус в правой части равенства указывает на то, что естественный отбор «стремится» снизить частоту аллеля A₂. Эффективность этого отбора, получившего название очищающего, тем выше, чем выше частота мутантного аллеля и степень его вредоносности (s).

Очевидно, что скорость появления в популяции мутантных аллелей пропорциональна частоте нормальных, из которых они возникают. Пренебрегая обратными мутациями, т. е. возникновением нормальных аллелей из мутантных, повышение доли аномальных аллелей за одно поколение можно оценить с помощью уравнения

?q = vp, (3.22)

где v — мутабильность локуса, р — частота нормального аллеля.

В то же время очищающий отбор снижает частоту мутантных аллелей со скоростью 0,5pqs за поколение (где s — средний коэффициент отбора против вредных мутаций). Поскольку оба процесса — мутирование и отбор — противоположны по своему эффекту на приспособленность популяции, то должна существовать точка мутационно-селекционного равновесия, когда поступление новых мутаций компенсируется их удалением из популяции очищающим отбором. Очевидно, в этой точке должно выполняться приближенное равенство

vp = 0,5pqs,

откуда можно оценить равновесную частоту вредного аллеля q:

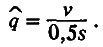
Эта частота прямо пропорциональна скорости появления вредных мутаций и обратно пропорциональна их среднему коэффициенту отбора. Поскольку природные популяции, несмотря на постоянно действующий процесс мутирования, не вымирают, то, очевидно, очищающий отбор со своей задачей успешно справляется. Между прочим, прямая оценка частот вредных мутаций в природных популяциях дрозофилы согласуется с уравнением (3.23).

Дрейф генов

Легко догадаться, что размер любой природной популяции не бесконечен хотя бы из-за ограниченности пищевых ресурсов. Ясно, что колебания в интенсивности таких факторов, как хищники, болезни и т. д., должны отражаться на численности особей. Тем не менее популяция, обитающая в одной и той же местности в течение нескольких тысяч лет, способна сохранять свою численность на более или менее постоянном уровне. Чтобы лучше уловить идею генетического дрейфа, примем, что размер популяции неизменен. Мы знаем, что каждая особь способна произвести (и действительно производит) очень много гамет, которые после оплодотворения могли бы дать начало большому числу потомков. Постоянство размера популяции означает, что в среднем одна особь производит всего две гаметы, дающих начало взрослым особям следующего поколения. Иными словами, в основе формирования генофонда популяции потомков лежит выбор 2N гамет из гигантского по объему гаметного фонда родителей. Насколько полно аллели этих выбранных гамет отражают генофонд популяции?

При случайном выборе из гигантского гаметного фонда всего 2N гамет (пусть даже ровно по две от каждой особи) аллельные частоты в генофонде потомков обязательно отклонятся от их значений в генофонде родителей. Отметим, что при случайном выборе двух гамет из всех производимых одной гетерозиготной особью мы точно отразим ее генотип лишь в 50 % случаев. В остальных 50 % обе гаметы будут нести только один аллель, другой будет потерян.

Интуитивно ясно, что при уменьшении объема гаметной выборки падает точность, с которой она отражает аллельный состав генофонда родителей. Специальный анализ показывает, что наиболее вероятное (среднеквадратическое) отклонение (?) частоты аллеля в обе стороны от исходной величины растет с уменьшением размера популяции, подчиняясь соотношению

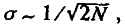
т. е. это отклонение обратно пропорционально квадратному корню из размера популяции.

Итак, на основании чисто статистических закономерностей частота каждого аллеля при смене поколений претерпевает сдвиг в совершенно непредсказуемом направлении. Этот феномен и представляет собой генный дрейф, его статистический характер не позволяет точно предсказать значения аллельных частот в популяции в ряду поколений. Более того, динамику изменения этих частот невозможно воспроизвести в принципе. Сколько бы раз мы ни следили за частотой какого-то аллеля, мы никогда не встретимся с двумя одинаковыми его судьбами.

Особое значение генный дрейф приобретает в вопросе о судьбе аллелей, не различимых естественным отбором. Такие аллели принято называть селективно-нейтральными или просто нейтральными. Сейчас мы увидим, что дрейф генов выступает как мощный фактор фиксации нейтральных аллелей. Проследим за динамикой частоты такого аллеля (A₁).

Пусть в популяции (будем считать ее популяцией нулевого поколения) исходная частота этого аллеля равна р₀.

Предположим, у нас есть возможность очень много раз проследить за динамикой изменения частоты аллеля А₁ в большом ряду поколений. Тогда, определяя его частоту (р₁) в популяциях первого поколения, в каждой из них мы обнаружим отклонение от значения р₀. Поэтому частоту аллеля А₁ в любой из популяций первого поколения можно представить как р₀ + ?р (?р — сдвиг частоты). Поскольку естественный отбор аллели не различает, вероятность изменения частоты аллеля А₁ в обоих направлениях одна и та же, т. е. среднее значение сдвига (где усреднение проведено по всем популяциям первого поколения) должно равняться нулю. Иными словами, средняя частота данного аллеля в совокупности популяций первого поколения <р₁> должна в точности равняться его исходной частоте в нулевом поколении.

Так как направление сдвига частоты аллеля А₁ сохраняет свою полную неопределенность и в последующих поколениях, то средняя частота этого аллеля <р₂> в совокупности популяций второго поколения не должна отличаться от <р₁>. Отсюда мы приходим к выводу, что в любом поколении средняя частота аллеля в совокупности популяций, происходящих от какой-то одной, остается равной частоте этого аллеля в исходной популяции, т. е.

р₀ = <р₁> = <р₂> =… (3.25)

Несмотря на то что в каждой популяции динамика изменения аллельных частот непредсказуема, мы можем с полной уверенностью утверждать, что рано или поздно такие изменения прекратятся. Могут быть только два финала: или частота аллеля возрастет до единицы, или она опустится до нуля. Достижение нуля означает потерю аллеля, а достижение единицы — его фиксацию. На рис. 11 приведено несколько судеб нейтральных аллелей, смоделированных компьютером. Каждая траектория частоты аллеля заканчивается либо нулем, либо единицей. Случайный характер изменения аллельной частоты напоминает движение броуновской частицы в трубке, на концы которой помещено клейкое вещество. Очевидно, что при своем блуждании частица когда-нибудь достигнет одного из концов трубки и там приклеится (зафиксируется). Итак, генный дрейф «стремится» уменьшить разнообразие аллелей, одна их часть теряется, а другая фиксируется.

Теперь рассмотрим совокупность всевозможных финалов частоты аллеля А₁. У части финальных популяций она будет равна единице, а у всех других — нулю. Очевидно, что доля популяций, зафиксировавших в конце концов аллель А₁ (иначе говоря, вероятность фиксации данного аллеля), равна его средней частоте в полной совокупности финальных популяций. Поскольку (см. формулу (3.25)) последняя должна равняться частоте аллеля в исходной популяции (р₀), мы приходим к нетривиальному заключению: вероятность фиксации нейтрального аллеля равна его частоте в генофонде популяции. Например, если эта частота равна 0,5, то аллель с равной вероятностью может или исчезнуть из популяции, или в ней зафиксироваться. Теперь перейдем к очень важному следствию — к судьбе только что возникшей мутации.

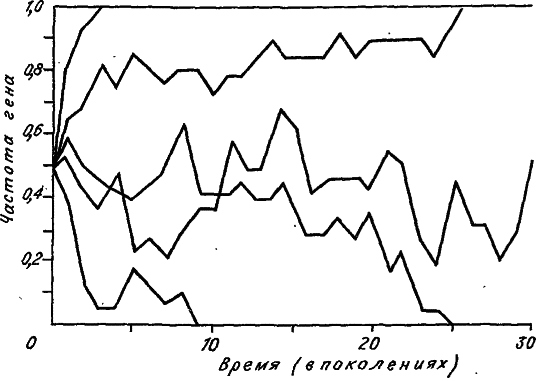
Рис. 11. Дрейф аллельных частот в пяти машинных экспериментах. Размер популяции N = 10. Исходная частота обоих аллелей 0,5 (по: [Kimura, 1983]).

Пусть в популяции возник совершенно новый нейтральный аллель. Очевидно, что его частота в момент возникновения равна 1/2N, поэтому и зафиксироваться с помощью дрейфа он может с той же вероятностью. Этот результат приводит нас к грустному выводу: фактически любой вновь возникший аллель обречен на исчезновение, поскольку вероятность этого события чрезвычайно близка к единице (1 — 1/2N). В то же время заметим, что процесс мутирования постоянно ведет к появлению новых аллелей. Если через V обозначить мутабильность локуса, то в каждом поколении в популяции должно появляться 2NV мутантных аллелей. Поскольку они не различаются естественным отбором, любой из них может зафиксироваться с вероятностью 1/2N. Значит, в данном случае скорость фиксации любого мутантного аллеля только за счет генного дрейфа должна равняться 2NV(1/2N). Обозначив скорость фиксации мутантного аллеля через К, приходим к очень простому уравнению

K = V. (3.26)

Этот изящный результат, полученный М. Кимурой в 1960 г., показывает, что в популяциях (вне зависимости от их размеров) может идти процесс фиксации новых аллелей, скорость которого определяется только скоростью мутирования локусов. Однако среднее число поколений, нужное для фиксации мутантного аллеля с помощью дрейфа, пропорционально размеру популяции и, как показал Кимура, оно близко к 4N.

Заметим, что геном любого вида содержит несколько тысяч локусов, поэтому в генофонде любой популяции только вследствие неизбежного генного дрейфа почти в каждом поколении фиксируются какие-то аллели. Однако подчеркнем, что этот вывод мы получили при допущении, что жизнеспособность организма не зависит от аллельного состава локусов; иными словами, естественный отбор эти аллели не различает. Несмотря на то что фиксация нейтральных аллелей занимает много времени, у данного процесса есть одна выгодная для популяции особенность — он проходит для нее совершенно бескровно.

Движущий отбор

До сих пор мы имели дело с панмиктической популяцией конечного размера, занимающей ограниченную территорию с фиксированными условиями среды. На самом же деле мир, в котором обитает популяция, изменчив, и идеально приспособиться к нему невозможно. Представим себе, что наша популяция в какой-то момент времени хорошо приспособлена к условиям своего существования, однако вдруг эти условия начали медленно, но неуклонно ухудшаться. В данной ситуации перед популяцией встает проблема огромной сложности: нужно не просто отбраковать относительно редкие мутантные аллели (чему в немалой степени помогает генетический дрейф), но и заменить старые, далеко не дефектные аллели на иные, более благоприятные, т. е. лучше соответствующие новым условиям среды.

Будем считать, что благоприятные мутации полудоминантны, т. е. h = 0,5. Если принять приспособленность гомозигот по старому аллелю (w₁₁) за единицу, то приспособленность гомозигот по благоприятному аллелю (w₂₂) должна равняться (1+s), а гетерозигот — (1+0,5s). По аналогии с рассмотренным выше случаем вредных мутаций, заменяя — s на +s, можно рассчитать среднюю приспособленность популяции (w) и среднюю приспособленность доноров благоприятного аллеля (w₂):

w = 1 + qs, (3.27)

w₂ = 1 + 0,5ps + qs, (3.28)

тогда сдвиг частоты благоприятного аллеля за одну генерацию можно определить по формуле

?q = (0,5pqs) / (1 + qs). (3.29)

При малых значениях q и s знаменатель в правой части этого уравнения мало отличается от единицы, поэтому с хорошей точностью должно выполняться соотношение

?q ? 0,5pqs, (3.30)

т. е. скорость возрастания частоты благоприятного аллеля в генофонде популяции прямо пропорциональна его частоте и селективному преимуществу.

Глядя на соотношение (3.30), можно подумать, что были бы в наличии благоприятные мутации, а процесс их фиксации — дело десятое. Однако анализ решения этого уравнения показывает, что даже при таком высоком коэффициенте отбора, как 0,1, для достижения частот благоприятного аллеля, близких к единице, требуется около 100 поколений, при s = 0,01 — не менее 1000.

В этих оценках мы не учитывали ограниченность размера реальных популяций. Кроме того, мы полагали, что каждый носитель благоприятной мутации имеет все возможности реализовать свое селективное преимущество. На самом же деле, разбиение вида на небольшие популяции является весьма эффективным средством не столько для фиксации, сколько для удаления редких аллелей — как нейтральных, так и благоприятных.

Для того чтобы новый благоприятный аллель вытеснил старый, нужно еще и простое везение. К сожалению, мы сейчас убедимся, что шансы на такое везение не очень велики. Представим себе, что в популяции сколь угодно большого, но постоянного размера возник благоприятный аллель А₂. Его носителем может быть только гетерозигота А₁А₂. Поскольку размер популяции постоянный, каждая особь передает в генофонд следующего поколения в среднем только две копии локуса А. Значит, гетерозигота А₁А₂может передать эти две копии в виде одной из трех комбинаций: А₁А₁, А₂А₂ и А₁А₂. Первая комбинация означает потерю аллеля А₂, вероятность этого события равна 25 %. В 50 % случаев в генофонд следующего поколения будет передана только одна копия мутантного аллеля (и в следующем поколении он может снова с вероятностью 25 % потеряться), а в 25 % случаев количество мутантных аллелей удвоится.

В этом рассуждении мы не учитывали эффекта статистического варьирования числа потомков каждого родителя. Точное решение задачи было получено выдающимся английским математиком и генетиком Р. Фишером. Он продемонстрировал, что вероятность потери вновь возникшей нейтральной мутации в первом же поколении равна 0,37 и быстро растет с увеличением числа поколений, стремясь в конечном счете к единице. Если же мутантный аллель сообщает его носителю селективное преимущество s в гомозиготном состоянии и 0,5s в гетерозиготном, то вероятность его фиксации численно близка к s. Итак, если коэффициент отбора в пользу носителя одной копии благоприятного аллеля составляет целых 5 %, то все-таки шансы его утратить равны 90 %. Следует заметить, что обычно s намного меньше единицы и даже меньше 0,1.

Положение может спасти лишь повторное возникновение благоприятных мутаций. Если скорость их возникновения равна v, то в популяции с размером N за одно поколение должно появляться 2Nv новых благоприятных мутаций, из которых будет фиксироваться доля, численно равная s. Отсюда скорость фиксации полудоминантных благоприятных мутаций (K) определяется уравнением

К = 2Nvs. (3.31)

Заметим, что здесь v обозначает не скорость мутирования вообще, а только скорость возникновения благоприятных мутаций. Если среди всех возникающих за поколение мутаций (V) благоприятные составляют долю f, то уравнение (3.31) можно слегка преобразовать:

К = 2NVfs. (3.32)

Эта формула хорошо передает особенность адаптивной эволюции. Ведь если число генов в геномах разных видов различается незначительно, то при приблизительном равенстве мутабильности локусов скорость адаптивной эволюции прямо пропорциональна доле благоприятных мутаций (среди всех возникающих) и средней степени их благоприятности. Если макроэволюция полностью сводима к микроэволюции, то уравнение (3.32) показывает, что для ускорения эволюции есть только два средства: увеличить селективное преимущество новых аллелей над старыми (s) и, главное, повысить «выход» благоприятных мутаций (f).

Плата за эволюцию

До сих пор мы рассматривали приспособленность как шансы зигот стать взрослыми организмами. Однако это понятие можно трактовать чуть-чуть иначе. В популяции постоянных размеров каждая особь оставляет в среднем одного взрослого потомка. Если особи с каким-то генотипом имеют повышенную или пониженную приспособленность, то это значит, что среднее число их потомков должно быть несколько больше или меньше единицы. Получается, что в популяции фиксированных размеров число взрослых потомков, оставляемых особью (ее мальтузианский параметр), может служить мерой ее приспособленности.

Мы знаем, что приспособленность популяции, в генофонде которой присутствует благоприятный аллель, за одно поколение немного возрастает, следуя за увеличением частоты данного аллеля. Но так как биомасса популяции увеличиться не может, то для сохранения прежней численности (в среднем один потомок на одного родителя) должно сократиться число потомков от обычных особей, не обладающих благоприятным аллелем. Иными словами, какая-то часть популяции должна остаться без взрослых потомков, что с генетической точки зрения эквивалентно ее гибели (случай так называемой генетической смерти). Очевидно, что это падение относительной приспособленности должно компенсироваться увеличением мальтузианского параметра у носителей благоприятного аллеля.

Процесс фиксации благоприятного аллеля обычно занимает много поколений, и на каждом из них имеет место гибель определенной доли популяции. Просуммировав эти доли по всем поколениям (с момента появления аллеля до его фиксации), можно получить величину так называемой платы за эволюцию. Количественную оценку этой суммы дал в 1957 г. знаменитый английский ученый-энциклопедист Дж. Холдейн. Он продемонстрировал, что плата за фиксацию полудоминантного благоприятного аллеля равна -2lnq₀ (q₀ — начальная частота аллеля). Иными словами, эта плата не зависит от коэффициента отбора, имеет значение лишь исходная частота благоприятного аллеля.

Если размер популяции равен миллиону особей, то частота благоприятного аллеля в момент его возникновения (1/2N) должна быть равна 0,5 * 10^-6. Удвоенный натуральный логарифм этой величины равен примерно 29, т. е. для реальных популяций его можно принять равным 30. Заметим, что снижение средней приспособленности на единицу означает генетическую смерть (не надо смешивать ее с обычной смертью) всех особей популяции. Получается, что за фиксацию (с помощью отбора) одного аллеля популяция должна «заплатить» 30-кратной генетической гибелью своих особей.

Это образное выражение совсем не следует понимать буквально. Биомасса эволюционирующей популяции остается на прежнем уровне, так как снижение относительной приспособленности носителей старого аллеля компенсируется повышением мальтузианского параметра у особей с благоприятным аллелем. Однако такое повышение не может превзойти возможностей особи к размножению — ее репродуктивного потенциала. Это обстоятельство ставит естественное ограничение на скорость адаптивной эволюции. Необходимость постоянно компенсировать генетическую гибель части популяции означает, образно выражаясь, увеличение нагрузки на репродуктивную функцию особей (во всяком случае, носителей благоприятного аллеля).

Теперь представим, что в популяции идет процесс фиксации сразу нескольких благоприятных аллелей. Ясно, что в этом случае плата за адаптивную эволюцию резко возрастает, что заставляет нас прийти к весьма пессимистическому выводу: популяция не в состоянии осуществлять параллельные адаптивные замещения аллелей сразу по нескольким локусам, поскольку дополнительная нагрузка на репродуктивный потенциал может превзойти возможности организма. Выходит, что благоприятные мутации скорее всего фиксируются популяцией не параллельно, а последовательно, т. е. адаптивная эволюция не может идти быстро.

Определенным выходом из «дилеммы Холдейна» могло бы явиться кооперативное, синергическое взаимодействие благоприятных мутаций. Подобное взаимодействие подразумевает, что две такие мутации повышают приспособленность больше, чем на простую сумму соответствующих коэффициентов отбора. В этом случае естественный отбор «хорошо видит» лишь комбинацию обоих мутантных генов и поэтому фиксирует их единым пакетом.

Генетический груз

В любой природной популяции всегда присутствуют вредные аллели, снижающие уровень ее приспособленности. Очищающий отбор «стремится» эти аллели удалить, но они снова появляются за счет вечно идущего процесса мутирования. Выше мы рассмотрели условия существования мутационно-селекционного равновесия. Для полудоминантных мутаций их равновесная частота довольно низка. Если в каком-то локусе скорость возникновения вредных мутаций равна 10^-6, а s ~ 0,03, то равновесная частота вредящих аллелей в генофонде составит всего 6*10^-5 (см.(3.23)). Казалось бы ничтожная доля, но ведь наше рассуждение подходит для всех локусов генома. Если это число равно 10 тысячам, то равновесная частота поврежденных аллелей при суммировании по всем локусам будет близка к 2/3. А если средняя скорость мутирования выше? Например, если средняя мутабильность локуса равна 10^-5, то можно прийти к заключению, что в природных популяциях вообще отсутствуют особи без дефектных аллелей.

Исследования японского генетика Т. Мукаи, проведенные на дрозофиле, свидетельствуют в пользу именно этого предположения. Мукаи проанализировал спектр мутаций, снижающих жизнеспособность мух, и обнаружил, что большая их часть представлена полудоминантными мутациями, снижающими приспособленность всего на 2–4 %, остальные мутации рецессивны и снижают в гомозиготном состоянии жизнеспособность мух практически до нуля. Общая скорость возникновения слегка вредящих мутаций составляет около 0,4 на гаплоидный геном (т. е. на гамету) за поколение.

Заметим, что Мукаи оценивал лишь мутации, снижающие жизнеспособность, тогда как приспособленность должна включать и другие ее компоненты (например, плодовитость). В связи с этим реальное число повреждающих мутаций, возникающих в каждом поколении в геноме гаметы, может оказаться близким к единице (если не больше). При такой интенсивности мутирования можно уже подумать об уровне приспособленности популяции. Если мутантов не слишком много, то понижение производства ими потомков вполне может быть скомпенсировано усиленным размножением особей, лишенных генетических недостатков. Этих последних назовем для удобства элитой.

Различие между числом потомков у элиты и среднестатистической особи отражает так называемый мутационный генетический груз (L), смысл которого ясен из формулы

L = (w_э — w) / w_э, (3.33)

где w_э — средняя приспособленность генетической элиты. Фактически генетический груз показывает, во сколько раз особь из элиты превосходит по мальтузианскому параметру среднюю особь популяции.

Теперь снова вернемся к реальной ситуации, когда в среднем каждая гамета получает одну вредную мутацию. Как с этим может справиться очищающий отбор? Здесь может показаться, что положение совершенно безвыходное, поскольку все гаметы оказываются бракованными, и элите не из чего возникнуть. Однако дело спасает случайный характер мутирования.

Распределение мутаций по гаметам равносильно распределению капелек дождя по плиткам мостовой. Пусть дождь был слабым, и на одну плитку в среднем упала одна капля, но это не означает, что на каждую плитку попало в точности по одной капле. Ясно, что на некоторые плитки упали две, на иные три капли, а часть плиток вообще осталась сухой. В теории вероятностей такая ситуация хорошо описывается законом Пуассона. В соответствии с ним доля сухих плиток равна е^-u. Здесь е — основание натуральных логарифмов, и — среднее число капель дождя, приходящееся на одну плитку. В нашем генетическом случае и — это число вредных мутаций, возникающее в среднем в одной гамете, поэтому доля гамет, счастливо избежавших мутаций, равняется е^-u, а доля зигот, возникших от слияния бездефектных гамет, составляет е^-2и. Отсюда следует, что для сохранения средней приспособленности популяции бездефектные особи должны размножиться в е^2и раз. В частности, при и = 1 каждая особь должна произвести не менее 7,39 потомков, что составляет довольно приличную нагрузку на репродуктивную способность элитных самок. А если эта величина еще больше?…

Однако вредные мутации могли бы удаляться не штуками, а сразу пакетами — по две, по три и т. д. Например, если вредная мутация рецессивна, то в гетерозиготном состоянии она не сказывается на приспособленности. Поэтому отбор «видит» только мутантную гомозиготу и, удаляя ее, освобождает генофонд сразу от двух экземпляров вредного аллеля. Если вредящий эффект мутации ощущается уже у гетерозиготы, то ее гибель унесет один вредный аллель, но заодно и один хороший. Следовательно, учитывая весьма широкое распространение слегка вредящих полудоминантных мутаций, природные популяции должны быть обременены весьма существенным генетическим грузом. Средством для его снижения мог бы быть кооперативный характер взаимодействия вредных аллелей разных локусов, когда вредящий эффект одной и той же мутации тем выше, чем больше подобных мутаций уже присутствует в геноме. При этом приспособленность особи по мере добавления мутаций падает по очень крутой параболе. Получается, что геном особи как бы накапливает вредные мутации, а при достижении какого-то порогового значения происходит резкое падение приспособленности; особь с таким геномом гибнет, освобождая генофонд популяции сразу от нескольких вредных мутаций.

По мысли советского генетика А.С. Кондрашова, деление особей на два пола является специальным изобретением для снижения генетического груза. Его расчеты показывают, что половой процесс, резко увеличивая размах изменчивости особей по числу вредных мутаций, позволяет популяции гораздо эффективнее освобождаться от последних.

Главный вывод, который мы должны сделать после ознакомления с проблемой генетического груза, заключается в том, что среднее число вредных мутаций, возникающих в одной гамете за поколение, не должно превышать определенной фиксированной величины и* (которая является произведением средней мутабильности генов на их число в геноме). Скорее всего уровень спонтанного мутирования в природных популяциях близок к этой критической величине. В пользу такого предположения свидетельствуют две группы фактов. Во-первых, скорость появления однотипных мутаций с качественным эффектом на фенотип у совершенно разных организмов довольно близка; во-вторых, оценка числа жизненно важных генов (потеря которых ведет к прекращению развития) в геноме таких эволюционно далеких видов, как дрозофила и мышь, дает в обоих случаях близкие значения (5—10 тысяч генов).

Заметим, что наличие верхнего предела в скорости мутирования (u*) равносильно существованию ограничения на рост информационного содержания генома. Это обстоятельство часто не учитывается многими молекулярными биологами, которые считают, что количество наследственной информации можно оценить исходя из содержания ДНК в гаплоидном ядре.

Медленные сдвиги среды

Итак, судьба разобщенных барьерами частей вида определяется соотношением двух процессов — экологической дифференциацией популяций и разрушением изолирующих барьеров. Находясь в несколько отличных экологических условиях, популяции под влиянием естественного отбора «стремятся» к ним лучше приспособиться, т. е. по ряду локусов зафиксировать разные аллели. Но этому стремлению противодействует генный поток, который, «просачиваясь» сквозь несовершенные барьеры, может вносить в каждую популяцию неблагоприятные (т. е. менее отвечающие местным условиям) аллели. Таким образом, генный поток выступает здесь как фактор, понижающий приспособленность каждой популяции, что позволяет говорить о миграционном генетическом грузе.

Есть только одно средство для закрепления успеха экологической дифференциации разделенных популяций — они должны за время своей изоляции стать разными видами, т. е. заменить географический барьер генетическим. Постоянное «стремление» вида расщепиться на несколько дочерних, по существу, представляет собой попытку вида освободиться от миграционного генетического груза. Кроме того, на периферии своего ареала вид может сталкиваться с качественно иными условиями среды, адаптация к которым означала бы прорыв вида в новую экологическую область.

Обрисованная здесь картина выглядит довольно оптимистично, но не следует забывать, что все эти адаптационные процессы предполагает фиксацию новых аллелей по десяткам локусов. Выше мы убедились в том, что на это требуются тысячи и даже десятки тысяч поколений. Но самое главное состоит в том, что естественный отбор проходит без селекционера, а где гарантии, что коэффициент отбора способен сохранять на протяжении нескольких тысяч поколений хотя бы свой знак? Иными словами, для адаптивной эволюции вектор естественного отбора должен сохранять направление и интенсивность в течение огромных отрезков времени. А учитывая противодействие со стороны генного потока, действие естественного отбора должно распространяться на значительную часть ареала вида, желательно на весь его ареал.

Естественный отбор — это метафора, его давление можно понимать как постепенное изменение интенсивности каких-то жизненно важных факторов в пространстве и (или) во времени. Например, если ареал вида соседствует с экологической областью, где уровень его абсолютной приспособленности на порядок ниже, то необходимо, чтобы такой контакт сохранялся в течение нескольких десятков тысяч поколений. Или же по всей территории, занятой видом, должно идти однонаправленное изменение какого-то жизненно важного параметра. Для адаптации к такой ситуации необходимо, чтобы скорость изменения параметра была очень небольшой. Во всяком случае, время перехода от оптимальных условий к очень плохим должно составлять тысячи или даже десятки тысяч лет.

О значении стабильности среды для экологической дифференциации, по-видимому, свидетельствует удивительное явление повышения численности видов большинства групп растений и животных в направлении от полюсов к экватору. Действительно, климат в тропиках гораздо стабильнее, чем в умеренных широтах. Достаточно вспомнить о недавнем оледенении, практически не отразившемся на животном и растительном мире экваториальной зоны.

Кроме того, многие жизненно важные параметры среды испытывают медленные колебания с периодом, исчисляемым миллионами и даже десятками миллионов лет. Так, за последние 220 млн лет климат на Земле сменялся циклически с теплого на холодный не менее 16 раз, примерно по 15 млн лет на цикл (рис. 12). Уровень мирового океана также подвержен циклическим изменениям. Только за последние 65 млн лет его уровень 8 раз изменялся на 100–250 метров. Еще более медленны, но более грандиозны орогенические (горообразовательные) циклы. В них можно выделить длительный геосинклинальный период с продолжительностью до 500 млн лет; за ним в течение примерно 50 млн лет идет период бурного поднятия коры, после которого в течение нескольких десятков миллионов лет может длиться возвращение к геосинклинальному периоду. Во время периода горообразования горы «вздымаются» со скоростью около одного миллиметра в год. В геосинклинальный период эрозия стачивает поднятия быстрее, чем они появляются. Осадки могут накапливаться в мелководных эпиконтинентальных морях со скоростью до одного километра за 10 миллионов лет. Все эти геологические явления, среди которых следует упомянуть еще и дрейф континентов, изменяют, характер морских и воздушных течений, а тем самым и климат многих областей.

Итак, данные геологии свидетельствуют о том, что на Земле действительно происходили и происходят очень медленные и однонаправленные изменения среды, захватывающие огромные территории. Характерное время таких изменений выражается миллионами лет.

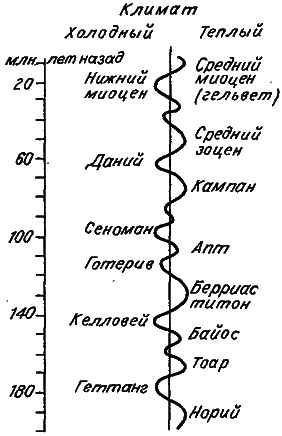
Рис. 12. Изменение среднегодовой температуры в течение юры и мела (по: [Красилов, 1977]).

Легко представить, что чем меньше ареал, занимаемый видом, тем больше у него шансов попасть под действие рассматриваемых здесь медленных однонаправленных сдвигов среды. Американский палеонтолог А. Буко проследил за изменением в течение силура и девона видового состава брахиопод, обитавших в разных геологических провинциях, по-видимому, просто в разных эпиконтинентальных морях. Оказалось, что единственным фактором, от которого зависела скорость изменения фауны, была площадь этих морей. Чем меньше площадь, тем быстрее изменялся состав брахиопод. Заметим, что речь идет о миллиардах особей, занимавших ареалы в миллионы квадратных километров.

Рассмотрев в этой главе обстоятельства, при которых возможны ненейтральные изменения генофонда вида, мы приходим к двум важным выводам: во-первых, уровень приспособленности вида к среде следует признать всего лишь удовлетворительным, и, во-вторых, скорость фенотипического сдвига (приспособительного характера) не может быть очень высокой.