Книга: Самая главная молекула. От структуры ДНК к биомедицине XXI века

Физики и математики за работой

Физики и математики за работой

Конечно, чтобы понять как следует, в чем состоит роль сверхспирализации, необходимо всесторонне изучить не только ее влияние на биологические функции ДНК, но и на физическую структуру молекулы. За дело взялись физики. Однако сразу же возникли серьезные проблемы. Разные физические методы, с помощью которых пытались измерить величину сверхспирализации, давали разные результаты.

Как-то в начале 1970-х годов Джером Виноград, открывший явление сверхспирализации и работавший в Калтехе (так называют сокращенно Калифорнийский технологический институт), встретил математика Брока Фуллера, также из Калтеха, и попросил его помочь разобраться в проблеме кольцевых ДНК, поскольку сам он к тому времени совершенно запутался. Фуллер живо заинтересовался рассказом Винограда. Он почувствовал, что здесь могут оказаться полезными некоторые результаты, как раз привлекшие внимание математиков в то время. Они касались неожиданной связи между топологией и дифференциальной геометрией.

Эти две области математики изучают одинаковые объекты, кривые и поверхности, но с абсолютно разных точек зрения. Дифференциальная геометрия исследует локальные свойства поверхности, такие как кривизна, кручение. Топологию, напротив, совершенно не интересуют эти характеристики, для нее имеет значение, например, есть ли в поверхности дырки (но не важно, какой формы эти дырки), сколько их и т. д. Так, мраморную статую может изучать и геолог, и искусствовед. Но геолога интересует только камень, а искусствоведа – форма, приданная камню скульптором. Вряд ли эти люди нашли бы между собой общий язык, подходя к делу строго профессионально.

Столь же неожиданной оказалась для математиков связь между дифференциально-геометрическими и топологическими характеристиками одного класса поверхностей – двусторонних полос. Знаменитый лист Мёбиуса – частный случай полосы. Чтобы смастерить лист Мёбиуса, возьмите полоску бумаги, перекрутите ее на 180° вдоль длинной оси и склейте концы полоски. Затем начните с любой точки и ведите карандашом линию, параллельную краям полосы. Вскоре вы увидите, что вернулись к исходной точке, ни разу не оторвав карандаша от листа. Это и есть замечательное, даже несколько загадочное свойство листа Мёбиуса – он имеет всего лишь одну сторону. Поэтому его называют односторонней полосой.

Теперь вырежьте еще полоску из бумаги и вновь склейте концы. Но при этом перекручивайте их не на 180°, как при склейке листа Мёбиуса, а на угол, равный т ? 360°, где т – целое число. Вы всегда будете получать двусторонние полосы. У двусторонней полосы два края представляют собой замкнутые кривые, причем они могут быть незацепленными или образовывать зацепление с каким-то значением порядка зацепления Lk, причем очевидно, что Lk = т.

Фуллер быстро сообразил, что с точки зрения математики молекула зкДНК представляет собой двустороннюю полосу. Краями полосы следует считать сахарофосфатные цепи молекулы. То, что зкДНК может быть только двусторонней полосой, – факт чисто химический, связанный с существованием направления в каждой из цепочек ДНК, причем комплементарные цепи направлены навстречу друг другу, т. е. антипараллельны (о чем мы поговорим подробно в конце этой главы). Легко убедиться, что если из такой молекулы попытаться склеить лист Мёбиуса, то ничего не получится – концы комплементарных цепей подойдут друг к другу в положении «голова к голове» и «хвост к хвосту», т. е. не смогут соединиться.

То, что сообщил Фуллер в статье, опубликованной вскоре после его разговора с Виноградом, состояло в следующем. Топологическая характеристика зкДНК, т. е. полосы, Lk не выражается однозначно через какую-либо геометрическую, а следовательно, и физическую характеристику молекулы. Она связана сразу с двумя геометрическими характеристиками. Первая хорошо известна в дифференциальной геометрии. Это кручение, осевая закрутка полосы Tw (от английского слова twist). Это есть суммарное количество оборотов, которое делает вектор, лежащий в плоскости полосы и перпендикулярный оси полосы, при движении вдоль полосы. Вторая характеристика не имела названия. Фуллер впервые дал ей имя – райзинг Wr (от английского глагола writhe, что значит скрючиваться, корчиться), так что модой давать экзотические названия, возникшей сначала в физике элементарных частиц (вспомните кварки, очарование, цвет и т. д.), постепенно заразились и математики.

Результат, приведенный Фуллером, был впервые строго доказан американским математиком Джеймсом Уайтом в 1968 году. Он устанавливает однозначную связь между Lk, Tw и Wr:

Поразительно то, что столь простая формула (она вполне могла бы принадлежать Гауссу) была открыта столь поздно. Она оказала неоценимую помощь в изучении свойств кольцевых ДНК. В чем же состоит значение этой, казалось бы, простой до примитивности формулы?

Прежде всего очень важно то, что величина Wr зависит только от формы, которую имеет ось полосы в пространстве, но совершенно не зависит от того, как полоса закручена вокруг своей оси. Далее, для Wr существует общая формула, позволяющая вычислить эту величину для любой кривой. Эта формула была известна очень давно и называется интегралом Гаусса, но истинный смысл этого интеграла как разности между Lk и Tw для полосы стал ясен только после построения теории полос.

Наконец, совсем необычно то, что в левой части формулы Уайта стоит величина, которая может принимать только целочисленные значения (это непосредственно следует из определения Lk – ведь количество протыканий поверхности не может быть не целым). В то же время обе величины, стоящие справа, могут принимать любые значения, вовсе необязательно целочисленные.

В этом месте может, даже должен возникнуть целый каскад недоуменных вопросов. Ведь величина Tw – это число оборотов, которые делает полоса вокруг своей оси. Почему же это не целое число, если полоса замкнута? Да и вообще, существует ли райзинг? Чем, собственно, Lk отличается от Tw? Не находим ли мы, вычисляя Lk и Tw, разными способами одну и ту же величину?

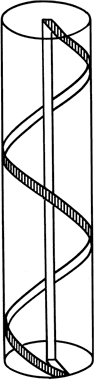
Рис. 29. Полоса, намотанная на цилиндр

Чтобы разобраться во всем этом, поставим опыт. Вырежем из бумаги узкую полоску шириной сантиметр. Обмотаем ею какой-нибудь цилиндрический предмет (типа того, как показано на рис. 29) несколько раз, причем сделаем это так, чтобы полоска при наматывании не закручивалась вокруг собственной оси. Затем чуть-чуть выдвинем концы полоски так, чтобы их можно было склеить. Это не вызовет сколько-нибудь значительной осевой закрутки.

Так мы получим замкнутую полосу, у которой, по самому способу ее получения, Tw = 0. Чему же будет равно Lk? Это можно выяснить теперь экспериментально. Возьмем ножницы, проткнем ими полоску в любом месте и разрежем ее вдоль по всей длине. Получатся две сцепленные друг с другом совсем узенькие полоски. Порядок их зацепления и есть Lk краев исходной полосы.

Вот и выходит, что можно создать Lk, не создав никакого Tw. То, что мы делали, когда обматывали полоску вокруг цилиндрического предмета, – это придавали ей райзинг. Равенство Lk = Tw справедливо тогда, когда ось полосы лежит на плоскости. Ощущение, что так должно быть всегда, основано на том, что мы обычно представляем себе полосу (или молекулу ДНК) так, будто ее ось описывает простую фигуру, скажем, окружность или что-то вроде того.

После статьи Фуллера стало ясно, что противоречия при исследовании сверхспирализации возникли потому, что одни методы измеряют физические характеристики, зависящие от Wr, а другие – от Tw. Получив в руки надежный математический аппарат, физики начали планомерно изучать влияние сверхспирализации на свойства зкДНК.

Как раз в то время в обиход стал входить метод гель-электрофореза, о котором мы говорили в главе 5. Была продемонстрирована очень высокая разрешающая способность метода при разделении молекул ДНК, имеющих разную длину. И тогда немецкому ученому Вальтеру Келлеру пришла в голову сумасшедшая идея: а что если попробовать разделить при помощи гель-электрофореза молекулы зкДНК с разными значениями Lk? Принцип разделения здесь должен быть совсем не тот, что для линейных молекул ДНК разной длины.

У молекул, отличающихся только числом сверхвитков (такие молекулы называют топоизомерами), длина будет одинакова. Следовательно, одинаковы будут и заряд, и действующая со стороны электрического поля сила. Однако скорость движения молекулы в геле определяется не только приложенной к ней силой, но и сопротивлением, которое она испытывает при движении. А это зависит в свою очередь от формы молекулы. Ясно, что если молекула имеет форму сильно переплетенной веревки, как на рис. 28, то она будет испытывать гораздо меньшее сопротивление среды при движении в поле, чем расправленная молекула. Иными словами, чем больше райзинг по абсолютной величине, тем быстрее должна двигаться молекула. Речь идет о райзинге, а не об Lk, потому что сопротивление среды определяется пространственной формой оси двойной спирали и не зависит практически от того, как закручена спираль вокруг оси.

Рассуждая таким образом, Келлер стал работать с гелем и вскоре показал, что если нанести на гель препарат сверхспиральной ДНК, выделенной из клетки, то получится набор отдельных полос, отстоящих друг от друга приблизительно на равные расстояния. Единственная дискретная характеристика зкДНК – величина Lk. Значит, молекулы ДНК, находящиеся в этих полосах, могут отличаться друг от друга только значением Lk, т. е. каждая полоса отвечает определенному топоизомеру. Скорее всего, соседние топоизомеры отличаются по значению Lk на единицу. Впоследствии было доказано, что так оно и есть.

Результат разделения молекул зкДНК, отличающихся по величине сверхспирализации, показан на рис. 30. Справа дан снимок геля после окончания электрофореза. Чтобы ДНК была видна, гель прокрашивают флуоресцирующим красителем, который прочно связывается с ДНК и как бы метит ее. Слева показан график зависимости интенсивности флуоресценции красителя от координаты вдоль геля. Можно видеть, насколько четкого разделения удается достичь. По таким картинкам нетрудно подсчитать величину сверхспирализации, отвечающую каждому топоизомеру.

В изучении кольцевых ДНК и сверхспирализации метод гель-электрофореза дал столь же много, как и в определении ДНКовых последовательностей. Было сделано множество тонких измерений, позволивших определить важнейшие характеристики зкДНК. Именно с помощью гель-электрофореза была точно определена энергия, которая может быть запасена в ДНК с помощью сверхспирализации.

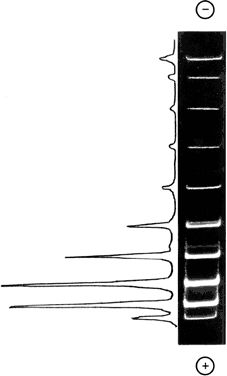
Рис. 30. Разделение молекул ДНК, отличающихся числом сверхвитков, методом гель-электрофореза. Опыт проводился с ДНК маленькой плазмидой рА03. содержащей 1683 пары нуклеотидов. Первоначально молекулы были нанесены сверху, вблизи отрицательной обкладки (это место не показано на рисунке)

Какие изменения в структуре ДНК может вызывать сверхспирализация? Понятно, что выгодным будет любое изменение структуры, в результате которого произойдет ослабление напряжения, вызванного в зкДНК сверхспирализацией. Поэтому было ясно, что сверхспирализация должна способствовать образованию в двойной спирали раскрытых областей, а также крестообразных структур. Крестообразные структуры в ДНК могут возникать в участках с последовательностями-перевертышами.

Что такое перевертыши? Они существуют в любом языке, не только в ДНКовом. Вот пример на русском языке: ИСКАТЬТАКСИ. Читайте эту фразу слева направо или справа налево – будет одно и то же (промежутки между словами и знаки препинания при составлении перевертышей не принимаются во внимание). А вот перевертыш подлиннее: НАЖАЛКАБАННАБАКЛАЖАН.

В свое время, когда поступили первые сообщения о существовании и возможной важной роли перевертышей в ДНКовых текстах (это было после открытия рестриктаз), началось повальное увлечение сочинением перевертышей на русском языке среди специалистов по ДНК. Мне очень нравится перевертыш, придуманный в то время Валерием Ивановичем Ивановым, известным специалистом по физике ДНК: РИСЛИНГСГНИЛСИР. Я представляю себе при этом короля и его дворецкого, торжественно провозглашающего: «Рислинг сгнил, сир!»

В ДНКовых текстах часто встречаются перевертыши. Из-за того, что ДНК состоит из двух цепей (т. е. как бы из двух параллельных, точнее, антипараллельных текстов), перевертыши могут быть двух типов. Такие перевертыши, как в обычном, одиночном тексте, называют зеркальными. В ДНК чаще встречаются перевертыши, которые читаются одинаково по каждой из цепей в направлении, заданном химическим строением ДНК (еще раз напомним, что две цепи ДНК имеют противоположное направление).

Практически всегда такими перевертышами бывают те участки, которые узнаются рестриктазами. Вот примеры (слева дано название рестриктаз; эти названия весьма причудливы, так как включают в себя первые три буквы названия бактерии, из которой выделена рестриктаза; стрелками показаны места разрезания ДНК рестриктазой):

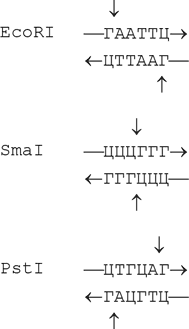
Так вот, замечательное свойство ДНКовых перевертышей состоит в том, что они могут образовывать крестообразные структуры. В самом деле, ведь обязательно левая половина перевертыша будет комплементарна правой, т. е. можно сделать так:

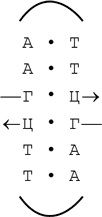
для места узнавания рестриктазой ЕсоRI и аналогично для любого другого перевертыша. Во всяком случае это не противоречит правилу комплементарности.

Однако сразу возникают вопросы. Разрешает ли структура ДНК существование таких резких изломов, какие должны возникнуть в двух вершинах креста? Ведь цепь ДНК обладает определенной жесткостью, не так просто сделать в ней резкий излом. В главе 3 мы уже обсуждали эту проблему в связи с укладкой ДНК в хромосомах. Двойная спираль – весьма жесткая штука, и для ее изгибания в хромосомах существуют специальные белки (гистоны и другие). Правда, одиночная цепь гораздо менее жесткая, так что вообще изломы в одиночной цепи возможны. Но они требуют затрат энергии. Поэтому совершенно неясно, зачем в ДНК будет возникать крест, если он может превратиться в регулярную двойную спираль. Но все это так в случае линейных молекул. А в сверхспирализованных?

Образование креста приводит к снятию сверхспирального напряжения. Не может ли это сделать выгодным образование креста в сверхспиральной ДНК? Какая сверхспирализация для этого необходима?

Чтобы ответить на все эти вопросы, группа теоретиков Института молекулярной генетики АН СССР – Вадим Аншелевич, Александр Вологодский, Александр Лукашин и автор этих строк – в 1979 году подробно проанализировала процесс образовании раскрытых и крестообразных структур в линейных и сверхспирализованных ДНК.[2] Теоретический анализ показал, что вероятность образования и раскрытых пар, и крестов в линейной ДНК очень мала. Особенно ничтожна вероятность возникновения креста – она порядка 10^–15, т. е. практически равна нулю. С ростом сверхспирализации картина очень сильно меняется. Быстро увеличивается вероятность образования раскрытых пар. Но вероятность образования крестов в коротких перевертышах вроде тех, которые узнаются рестриктазами, остается пренебрежимо малой при любых значениях сверхспирализации.

Другое дело – более длинные перевертыши, содержащие 15–20 или более пар. Такие перевертыши редко, но встречаются в ДНК. Вот, например, перевертыш из плазмиды Соl Е1, он показан на рис. 31. Для таких длинных перевертышей вероятность образования крестов растет, согласно расчетам, фантастически резко с ростом сверхспирализации. При нормальных значениях сверхспирализации, типичных для многих ДНК, вероятность образования креста оказывается порядка единицы, т. е. становится в 10¹⁵ (миллион миллиардов!) раз больше, чем в линейной молекуле. После того как наши теоретические предсказания были опубликованы, многие экспериментаторы принялись искать крестообразные структуры в зкДНК. Первыми финишировали две команды – британская (Дэвид Лилли) и американская (Роберт Уэллс). Им удалось доказать, что длинные перевертыши в сверхспиральных ДНК действительно образуют кресты.

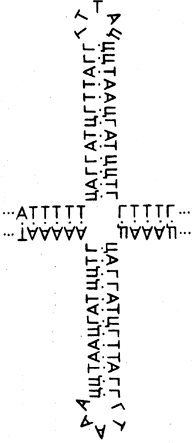
Рис. 31. Такой крест образуется в ДНК Co1 Е1. когда она находится в сверхспиральном состоянии

Как же удалось это сделать? Ведь сами шпильки, возникающие в крестообразных структурах, слишком малы, чтобы их можно было разглядеть даже в электронный микроскоп. Поэтому для поиска крестов был применен такой прием. Сверхспирализованную ДНК обрабатывали ферментом – однонитевой эндонуклеазой. Этот фермент рвет только одиночную цепь ДНК, но не трогает двойную спираль. Поэтому обычную линейную, или кольцевую замкнутую, но не сверхспирализованную молекулу фермент не разрывает. Оказалось, однако, что сверхспирализованную ДНК он разрывает, причем в строго определенном месте. Определили последовательности нуклеотидов слева и справа от места разрыва. Оказалось, что во всех случаях разрезание шло строго в середине больших перевертышей, именно тех, в которых, согласно теоретическим расчетам, должны образовываться кресты. Такие опыты, казалось бы, могут иметь только одно объяснение: в сверхспирализованных ДНК в местах длинных перевертышей двойная спираль с большой вероятностью превращается в крестообразную структуру; однонитевая эндонуклеаза разрывает образующиеся при этом в вершинах креста однонитевые петли.

Однако вскоре возникли сомнения. Образуются ли кресты на самом деле в ДНК или они возникают лишь под действием белка, однонитевой эндонуклеазы? Чтобы рассеять эти сомнения, необходимо было зарегистрировать образование крестов каким-либо другим методом, без фермента. Но, как уже говорилось выше, непосредственно увидеть кресты нельзя даже под электронным микроскопом. Как же быть?

Вновь на помощь пришел метод гель-электрофореза. Воистину нет цены тем услугам, которые эта удивительно простая методика оказала и продолжает оказывать тем, кто занимается ДНК. Мы привыкли к тому, что научный прогресс немыслим без сложнейших, дорогостоящих установок, начиненных сверхсовременной электроникой, сверхмощными компьютерами, лазерами и бог знает чем еще. Эти установки многие годы разрабатывают мощные фирмы с многотысячным персоналом, и стоят они десятки и сотни тысяч долларов. А вот представьте себе, что вы попали в лабораторию 1980-х годов, где проводились работы по изучению структуры ДНК, пользующиеся широкой известностью, и попросили показать экспериментальную установку, на которой эти работы были выполнены. Вы были бы поражены. Вас бы провели в комнату, в которой ничего не было, кроме обычного химического стола. Среди всяких склянок с реактивами вам показали бы небольшую, явно самодельную прозрачную коробку из плексигласа, частично заполненную водой, от которой отходят два тоненьких провода. И все. И вам еще сказали бы, что в это самое время на этой установке идет важный опыт. Вы почувствуете себя одураченным, как на выступлении хорошего фокусника. «Не может быть, – воскликнули бы вы, – чтобы с помощью такой примитивной штуки можно было решать тончайшие вопросы структуры ДНК, которые не помогают выяснить ни самые мощные электронные микроскопы, ни другие чудеса современной техники! Это какой-то обман».

Никакого обмана нет. Просто, как в любом хорошем фокусе, самого главного не разглядишь. Разумеется, этот волшебный ящик был бы совершенно бесполезен, если бы в нем не лежала прозрачная пластинка геля, а на гель не был бы наслоен образец ДНК, который вы, конечно, не могли заметить. И весь фокус в том, что это за ДНК. Она была специально приготовлена с использованием самых изощренных методов генной инженерии. Прежде чем попасть в этот неказистый приборчик, ДНК прошла через руки многих людей, крупнейших экспертов в своем деле, разбросанных по лабораториям в разных частях света. И каждый использовал все свои знания, все свое умение, чтобы изменить свойства этой ДНК нужным ему образом. Наконец, где-то в одной из соседних комнат были проведены последние приготовления ДНК к запланированному опыту. Вот вам и разгадка фокуса. В последние десятилетия успех в исследовании структуры ДНК стал невозможен без освоения специалистами по структуре ДНК методов генной инженерии.

Но вернемся к крестам. Использование метода гель-электрофореза для регистрации крестов в ДНК основано на том, что в результате перехода участка ДНК, имеющего последовательность-перевертыш, в крестообразное состояние, происходит частичное снятие сверхспиральных напряжений в молекуле. Молекула расправляется, становится менее сверхскрученной и начинает медленнее двигаться в геле под действием электрического поля из-за большего сопротивления среды. В результате топоизомер, в котором образовался крест, оказывается на электрофореграмме, типа приведенной на рис. 30, выше, чем топоизомер, имеющий на единицу меньшее число отрицательных сверхвитков, но не несущий креста. Так что в случае образования крестов должна нарушаться регулярная «лесенка», в которой топоизомеры с ростом отрицательной сверхспирализации движутся все быстрее и быстрее. Происходит наложение двух «лесенок» – отвечающих топоизомерам без крестов и с крестами. В результате на опыте возникает довольно сложная картина полос, в которой легко запутаться.

Разобраться в этой картине помогает остроумный прием, придуманный в начале 1980-х годов и получивший название «двумерный гель-электрофорез».

Опыт проводят не в столбике геля, как в случае традиционного, одномерного гель-электрофореза, а в квадратной пластинке из геля. На один из углов пластинки наслаивают образец ДНК и к двум противоположным сторонам квадратной пластинки прикладывают электрическое поле. В результате получают систему полосок, идущих вдоль одной из сторон пластинки. Эта картина тождественна той, которая получается при одномерном гель-электрофорезе. Теперь электроды переключают так, чтобы электрическое поле было перпендикулярно тому полю, в котором проводили первое разделение. При этом гель насыщают молекулами хлорокина. Эти молекулы связываются с двойной спиралью ДНК и уменьшают осевую закрутку (т. е. величину Tw). Связывание приводит к резкому уменьшению сверхспирального напряжения во всех топоизомерах образца, и его оказывается недостаточным, чтобы вызвать образование крестов. Кресты исчезают, и, следовательно, при гель-электрофорезе во втором направлении должна образоваться только одна, регулярная «лесенка». То, что в результате получается, видно на рис. 32.

Самое главное в этой картине – это то, что в регулярном следовании пятен происходит разрыв. В том, что во всех топоизомерах, идущих после разрыва, действительно возник крест, легко убедиться с помощью однонитевой эндонуклеазы. Если провести двумерный электрофорез после обработки препарата ДНК однонитевой эндонуклеазой, то на получившейся картине исчезают все пятна, следующие после разрыва. Это происходит потому, что эндонуклеаза атакует однонитевые петли креста и рвет их. ДНК перестает быть замкнутой, топологические напряжения снимаются, и все топоизомеры превращаются либо в расправленные кольца, либо (после длительной обработки однонитевой эндонуклеазой) в линейные молекулы.

Если далее локализовать место разрыва на молекуле ДНК, то оказывается, что эндонуклеаза наносит разрыв в точности в центре главного палиндрома. Такие опыты, проведенные впервые Виктором Лямичевым и Игорем Панютиным все в том же Институт молекулярной генетики АН СССР, окончательно рассеяли всякие сомнения в том, что кресты действительно самопроизвольно возникают в ДНК при достаточной отрицательной сверхспирализации. Эти опыты также продемонстрировали, что наши теоретические предсказания вероятности образования крестов в сверхспиральных ДНК верны количественно.

Рис. 32. Типичная картина двумерного гель-электрофореза, наблюдаемая при образовании в ДНК крестообразных или других альтернативных структур, о которых речь будет идти в главе 9. Специально приготовленная смесь различных топоизомеров одной и той же ДНК, несущей вставку, способную переходить в альтернативную структуру, была помещена в левый верхний угол квадратной пластинки геля. Затем было приложено электрическое поле так, чтобы молекулы ДНК двигались сверху вниз вдоль левого края пластинки. После завершения разделения топоизомеров в первом направлении гель насыщали молекулами хлорокина, которые уменьшают сверхспиральное напряжение. Концентрацию хлорокина подбирали с таким расчетом, чтобы сверхспирального напряжения было недостаточно для образования альтернативной структуры. Затем направление электрического поля меняли так, чтобы молекулы двигались слева направо. В результате последовательность пятен во втором направлении соответствовала последовательности топоизомеров.

Самое верхнее пятно отвечает нулевому топоизомеру, т. е. релаксированной, несверхспирализованной ДНК. Пятна, следующие от этого пятна по часовой стрелке, отвечают положительным топоизомерам, а те, что против часовой стрелки, – отрицательным. Ясно виден скачок подвижности, наблюдающийся в данном случае между топоизомерами –10 и –12. Это означает, что в топоизомерах –12, –13,… альтернативная структура присутствует, а в топоизомерах…, –9, –10 она отсутствует. Топоизомер –11 занимает промежуточное положение – в нем альтернативная структура то образуется, то исчезает

Какова роль крестов в ДНК? Пока об этом ничего не известно. Думают, что крестообразные структуры могут служить местами посадки на ДНК каких-то белков. Во всяком случае кресты – это первый надежно доказанный пример того, что структура отдельных участков биологически активной ДНК может существенно нарушаться при условиях, близких к тем, в которых ДНК функционирует в живой клетке. Насколько важную роль играют эти и, возможно, другие нарушения, о которых будет рассказано в главе 9, в работе ДНК в клетке – это вопрос дальнейших исследований.