Книга: Астероидно-кометная опасность: вчера, сегодня, завтра

Таблица 7.6. Влияние принятых значений ускорения, вызываемого эффектом Ярковского, на величину минимального расстояния от Апофиса до Земли и смещение астероида вдоль орбиты на 13 апреля 2029 г.

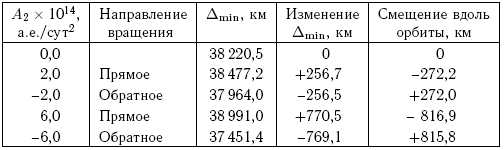
Изменения смещения вдоль орбиты при A₂ = (+6,-6) 10^-14 а.е./сут² близки к оценкам, полученным в работе [Giorgini et al., 2008]. Конечно, подобные расчеты имеют только качественный характер, поскольку реальное значение A₂ из имеющихся наблюдений найти невозможно. Но метод может быть использован в будущем, если будет получено необходимое число достаточно точных наблюдений.

Оценим теперь, как влияет эффект Ярковского на положение эллипса рассеяния на плоскости цели и на вероятность столкновения Апофиса с Землей в 2036 г. Будем исходить из предположения, что величина A₂ для астероида равна -2 10^-14 а.е./сут², что приводит к сокращению его полуоси и к увеличению среднего движения. В результате к апрелю 2029 г. астероид сместится вдоль орбиты на величину +272 км (табл. 7.6). Таким образом, астероид, соответствующий номинальному решению, найденному с учетом дополнительного ускорения, пересечет плоскость цели несколько раньше, и его минимальное расстояние от Земли составит, как показано в табл. 7.6, 37 964 км по сравнению с расстоянием в 38 220,5 км, на котором астероид должен проследовать мимо Земли в 2029 г. согласно решению, полученному ИПА.

7.7.7. Перспективы уточнения орбиты Апофиса. Для планирования возможного изменения орбиты Апофиса в случае, если это изменение будет вести к неизбежному или весьма вероятному столкновению, важно иметь представление о том, каковы перспективы проведения дальнейших астрометрических и физических наблюдений данного астероида и какого уточнения модели движения астероида можно ожидать в предстоящий период. При рассмотрении данного вопроса важно иметь в виду, что активные действия по изменению орбиты Апофиса должны быть предприняты до 2029 г. Величина корректирующего одиночного импульса, прикладываемого к астероиду до апреля 2029 г., чтобы избегнуть столкновения в 2036 г., примерно на три порядка меньше необходимого импульса после сближения в 2029 г. [Ивашкин, Стихно, 2008]. Причина такого различия вполне понятна. В случае, если коррекция выполняется до 2029 г., необходимо лишь несколько изменить минимальное геоцентрическое расстояние астероида (изменить орбиту так, чтобы ее пересечение с плоскостью цели произошло вне ближайшей окрестности «замочной скважины» размером около 600 м). Остальную работу по изменению траектории выполнит гравитационное поле Земли. После 2029 г. гелиоцентрическую орбиту астероида придется смещать уже на величину порядка нескольких радиусов Земли.

Размеры астероида и особенности его орбиты таковы, что благоприятные условия для его наблюдения складываются лишь в определенные весьма непродолжительные периоды времени. На рисунках 7.6–7.8 показаны элонгация астероида Апофис от Солнца, его звездная величина и расстояние от Земли в период 2006–2024 гг. На протяжении 2009–2011 гг. видимая звездная величина астероида будет оставаться в пределах 19,5^m–22,1^m. Но относительно большой блеск имеет место при малых элонгациях от Солнца. Сомнительно, что при звездной величине, превышающей 21^m, астероид можно будет наблюдать в элонгациях, меньших 50°. Таким образом, ближайшее «окно» для оптических наблюдений откроется не ранее декабря 2011 г., когда элонгация превысит 50°, а звездная величина будет меньше 21^m.

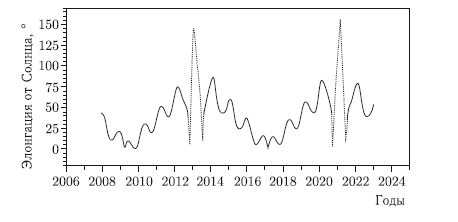
^{Рис. 7.6. Элонгация астероида Апофис от Солнца}

Возможности проведения новых радиолокационных наблюдений Апофиса также очень ограничены. Для наиболее крупного 300-м радиолокатора в Аресибо (Пуэрто-Рико, США) предельно возможное расстояние приема отраженного от астероида сигнала (при заданных размерах астероида и значении радиоальбедо его поверхности) составляет 0,31 а.е. Для 70-м локатора в Голдстоуне (США) расстояние приема составляет всего 0,14 а.е.

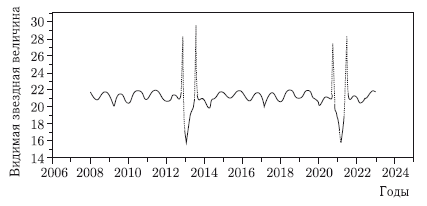
^{Рис. 7.7. Видимая звездная величина астероида Апофис}

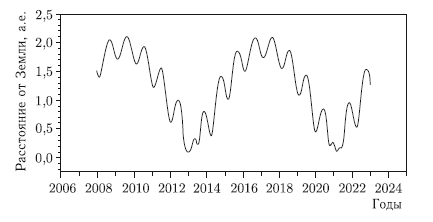
^{Рис. 7.8. Расстояние от астероида Апофис до Земли}

Примерно такие же возможности имеются у радиолокатора в Евпатории и модернизируемого радиотелескопа в Уссурийске. Таким образом, «окна» для радиолокационных наблюдений будут открыты только в конце 2012 г. — первой половине 2013 г., в октябре 2020 г. и феврале — августе 2021 г.

В работе [Chesley, 2005] предпринята попытка оценить, насколько точно может быть определена орбита Апофиса из возможных оптических и радиолокационных наблюдений, при условии, что из них будет получена не только астрометрическая информация о положениях Апофиса, но и найдено положение оси и направление вращения астероида. Как отмечалось ранее, две последние величины важны для оценки влияния эффекта Ярковского на движение астероида. В работе предполагается, что в периоды, наиболее благоприятные для наблюдений, каждую вторую ночь будет получено одно астрометрическое наблюдение со средней ошибкой в 0,2?, а в периоды, когда наблюдения будут менее доступны, но все еще возможны для крупных телескопов, одно наблюдение с той же ошибкой будет получено в течение каждой лунации. Далее предполагается, что в периоды 14–20 февраля и 6–10 июля 2013 г., а затем в периоды 9–12 октября 2020 г. и 16–20 марта 2021 г. с помощью радиолокатора в Аресибо будет выполнено в сумме 23 измерения расстояния до астероида с различной точностью в зависимости от расстояния. С учетом уже имеющихся наблюдений и предположительно осуществленных к исходу того или иного интервала можно оценить, с какой точностью определяется большая полуось эллипса рассеяния на плоскости цели в 2029 г. по всем имеющимся на рассматриваемый момент наблюдениям. Из вычислений Чизли следует, что к началу 2014 г. большая полуось эллипса рассеяния сократится примерно до 30 км, а к началу 2022 г. — до величины, несколько превышающей 10 км, если радарные наблюдения осуществлены не будут, и до 1 км, если они будут выполнены. Кроме того, в работе Чизли моделируется уточнение эллипса рассеяния с учетом годичного приема радиосигналов с эквивалентной точностью ±2 м от передатчика, доставленного на Апофис в 2019 г. С учетом радионаблюдений точность определения большой полуоси эллипса рассеяния повысится до 100 м.

В работе [Giorgini et al., 2008] эта проблема также обсуждается, но с применением иных подходов. Впрочем, результаты в целом оказываются сопоставимыми.

Можно поставить вопрос: какова вероятность того, что с учетом всех факторов столкновение с Апофисом в 2036 г. произойдет, и как вероятность столкновения будет эволюционировать с течением времени? Можно попробовать найти ответ на этот вопрос, если еще раз обратиться к рис. 7.5. Мы уже видели, что «замочная скважина» для столкновения в 2036 г. располагается на расстоянии 1444,7 км = 4,11?_? от центра эллипса, что определяет малую вероятность столкновения. Но при этом не был принят во внимание эффект Ярковского. Он способен сдвинуть центр эллипса, а вместе с ним и весь эллипс рассеяния вдоль большой оси в ту или иную сторону. Направление смещения и его величина зависят от положения оси вращения астероида. Если наклон оси вращения к плоскости орбиты астероида меньше 90° (прямое вращение), то, как нетрудно видеть, реактивный эффект покидающих тело тепловых фотонов имеет составляющую, направленную по вектору орбитальной скорости тела (рис. 7.9).

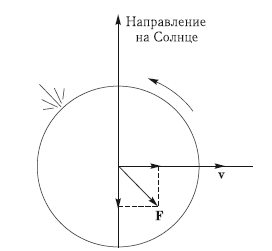
^{Рис. 7.9. Эффект Ярковского в случае прямого вращения астероида; F — вектор реактивного ускорения, v — орбитальная скорость астероида}

Это приводит к увеличению большой полуоси орбиты астероида и уменьшению его среднего движения. Астероид будет двигаться по орбите с некоторым отставанием во времени и догонит плоскость цели 13 апреля 2029 г., несколько позже по сравнению с невозмущенным случаем. Из этого следует, что координата ? центра эллипса окажется больше и астероид пройдет мимо Земли на несколько большем расстоянии от ее центра и от «замочной скважины» (положение последней в возмущенном случае останется практически тем же). В случае обратного осевого вращения астероида все будет обстоять с точностью до наоборот. Астероид пересечет плоскость цели в более ранний момент времени по сравнению с невозмущенным случаем, и весь эллипс как целое сместится в сторону меньших геоцентрических расстояний. По расчету [Giorgini et al., 2008] эффект Ярковского может привести к смещению астероида вдоль орбиты на величину от 325 км до 740 км в зависимости от принятых значений радиуса, плотности вещества и коэффициента теплопроводности. Можно рассчитать, что значение координаты ? при этих смещениях вдоль орбиты изменится на величины того же порядка. При прямом направлении вращения это означает, что расстояние от центра эллипса до «замочной скважины» возрастет на указанные величины и что столкновение практически невозможно (вероятность столкновения меньше 10^-7). При обратном направлении вращения эффект Ярковского способен сдвинуть эллипс рассеяния так, что «замочная скважина» окажется в пределах 3a_?. Вероятность столкновения в этом случае остается малой, но заметно отличной от нуля.