Книга: Гиперпространство: Научная одиссея через параллельные миры, дыры во времени и десятое измерение

Возрождение теории Калуцы – Клейна

Возрождение теории Калуцы – Клейна

Эту проблему называли «величайшей в науке всех времен». В прессе ее именовали святым Граалем физики, стремлением объединить квантовую теорию и гравитацию, тем самым создав «теорию всего». Эта задача не давала покоя самым блистательным умам XX в. Не вызывало сомнений, что решивший ее будет удостоен Нобелевской премии.

К 1980-м гг. физика зашла в тупик. Сила гравитации упрямо держалась особняком от трех других сил. Парадоксально, но, несмотря на то что первое представление о классической теории гравитации физики получили благодаря трудам Ньютона, к пониманию квантовой теории гравитации они пришли в последнюю очередь (из всех теорий взаимодействия).

Все корифеи физики пытались решить эту задачу, но безуспешно. Эйнштейн посвятил единой теории поля последние 30 лет своей жизни. Даже великий Вернер Гейзенберг, один из основателей квантовой теории, конец жизни посвятил попыткам создать свой вариант единой теории поля и опубликовал труд, посвященный этому предмету. В 1958 г. Гейзенберг объявил по радио, что ему вместе с его коллегой Вольфгангом Паули наконец удалось разработать единую теорию поля, недостает лишь некоторых технических деталей. (Когда пресса распространила это ошеломляющее заявление, Паули пришел в ярость – из-за того, что Гейзенберг поспешил. Паули отправил соавтору письмо, в которое вложил чистый лист бумаги с подписью: «Вот доказательство, что я умею рисовать, как Тициан. Недостает лишь технических деталей»{51}.)

Позднее в том же году Вольфганг Паули наконец прочел лекцию по единой теории поля Гейзенберга – Паули в присутствии физиков, жаждущих услышать недостающие подробности. Однако лекцию восприняли неоднозначно. Наконец, Нильс Бор поднялся и заявил: «Все мы единодушны в том, что ваша теория безумна. Мы расходимся лишь в вопросе о том, достаточно ли она безумна»{52}. Попыток осуществить «окончательный синтез» предпринималось столько, что они породили ответный скептицизм. Лауреат Нобелевской премии Джулиан Швингер сказал: «Это не что иное, как очередной симптом болезни, которой страдает каждое поколение физиков, – непреодолимое желание получить ответы на все фундаментальные вопросы еще при жизни»{53}.

Но к 1980-м гг. «квантовая теория дерева» после полувека почти непрерывного успеха начала выдыхаться. Я отчетливо помню, какая атмосфера досады и раздражения царила в то время среди приунывших молодых физиков. Всем казалось, что Стандартную модель погубил ее же собственный успех. Она была настолько удачна, что каждая международная физическая конференция воспринималась как очередная печать одобрения. Все разговоры сводились к очередному успеху в скучном эксперименте со Стандартной моделью. На одной физической конференции я обернулся, чтобы взглянуть на зал, и обнаружил, что половина слушателей уже дремлет; между тем оратор продолжал бубнить и показывать одну схему за другой, демонстрируя способ увязать последние полученные данные со Стандартной моделью.

Я чувствовал себя как физики на рубеже веков. Они тоже, по-видимому, зашли в тупик. На протяжении десятилетий они занимались нудным делом, вписывали в таблицы данные по спектральным линиям разных газов или же решали уравнения Максвелла для все более сложных металлических поверхностей. Поскольку в Стандартной модели девятнадцать незаданных параметров, которые можно произвольно «настроить» на любую величину, как волну в радиоприемнике, мне представлялось, что физики потратят еще несколько десятилетий на поиски точного значения всех девятнадцати.

Пришло время совершить революцию. Следующее поколение физиков манил мир «мрамора».

И конечно, на пути к истинной квантовой теории гравитации возникло несколько серьезных проблем. Одна из проблем создания теории гравитации заключается в том, что сила этого взаимодействия ужасающе мала. К примеру, требуется масса всей Земли, чтобы удерживать обрывки бумаги на моем столе. Но расческой, которой я только что причесался, я могу поднять со стола эти бумажки, преодолевая силу планеты Земля. Электроны моей расчески гораздо мощнее силы притяжения целой планеты. А если мне понадобится сконструировать «атом» с электронами, притянутыми к ядру силой гравитации, а не электрической силой, такой атом должен будет иметь размеры Вселенной.

Обычно мы считаем силу гравитации пренебрежимо малой по сравнению с силой электромагнитного взаимодействия, следовательно, с огромным трудом поддающейся измерению. Но при попытке записать квантовую теорию гравитации ситуация меняется. Квантовые поправки, обусловленные гравитацией, сопоставимы с планковской энергией, или 1019 млрд эВ, т. е. значительно превосходят все возможности, достижимые на планете Земля в данном веке. Запутанность ситуации усугубляется при попытке построить исчерпывающую теорию квантовой гравитации. Как мы помним, специалисты по квантовой физике пытаются проквантовать силу: они разбивают ее на мелкие порции энергии, называемые квантами. При бессистемном квантовании теории гравитации ее функция постулируется как обмен мелкими порциями гравитации, или гравитонами. Стремительный обмен материи гравитонами – вот что удерживает ее от гравитационного распада. В этой модели нам не дает оторваться от пола и улететь в космос со скоростью тысячу миль в час незримый обмен триллионами крохотных частиц-гравитонов. Но всякий раз, когда физики пытались произвести простые расчеты, чтобы вычислить квантовые поправки к законам гравитации Ньютона и Эйнштейна, они обнаруживали, что результат бесконечно велик и, следовательно, бесполезен.

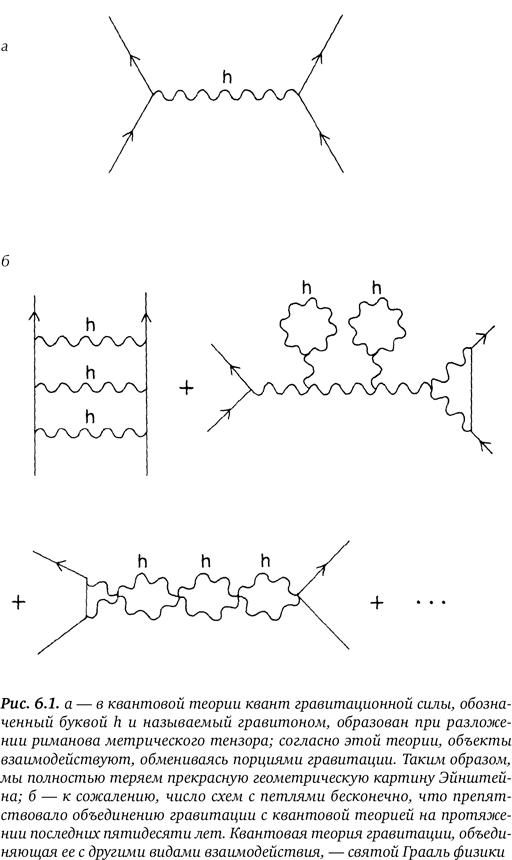
Посмотрим, к примеру, что происходит при столкновении двух электрически нейтральных частиц. Для того чтобы получить диаграмму Фейнмана для данной теории, нам понадобится приближение, поэтому предположим, что кривизна пространства-времени, а значит, риманов метрический тензор приближается к единице. Предположим, что пространство-время неискривленное, почти плоское, тогда можно разложить компоненты метрического тензора как g₁₁ = 1 + h₁₁, где 1 – плоское пространство в нашем уравнении, а h₁₁ – поле гравитона. (Эйнштейн, конечно, пришел бы в ужас, узнав, как специалисты по квантовой физике уродуют его формулы, разбивая метрический тензор. Это все равно что взять прекрасную мраморную глыбу и разбить ее кувалдой.) Совершив это насилие, мы получаем квантовую теорию в традиционном виде. На рис. 6.1, а мы видим, что две нейтральные частицы обмениваются квантами гравитации, обозначенными полем h.

Проблема возникает при обобщении всех диаграмм с петлями: мы видим, что они расходятся, как на рис. 6.1, б. Для поля Янга – Миллса мы могли бы с помощью хитроумных фокусов перетасовывать все эти бесконечные величины, пока не сократим их или не получим величины, не поддающиеся измерению. Однако можно продемонстрировать, что обычные способы перенормировки не срабатывают, если мы применяем их к квантовой теории гравитации. Более чем полувековые старания физиков каким-либо способом избавиться от этих бесконечностей оказались тщетными. Другими словами, попытки сокрушить «мрамор» с помощью грубой силы потерпели крах.

А потом в начале 80-х гг. XX в. возникло любопытное явление. Как мы помним, теория Калуцы – Клейна не находила применения на протяжении 60 лет. Но физики были настолько раздосадованы неудачными попытками объединить гравитацию с другими квантовыми взаимодействиями, что начали преодолевать предубежденность по отношению к незримым измерениям и гиперпространству. Они были готовы на альтернативный вариант, и таковым оказалась теория Калуцы – Клейна.

Ныне покойный физик Хайнц Пейджелс так вспоминал ажиотаж вокруг возрождения теории Калуцы – Клейна:

Даже нобелевский лауреат Стивен Вайнберг с энтузиазмом встретил ренессанс теории Калуцы – Клейна. Но нашлись и такие физики, которые скептически отнеслись к ее возрождению. Напоминая Вайнбергу, как трудно экспериментальным путем измерить эти компактифицированные измерения, Говард Джорджи из Гарварда сочинил следующий лимерик:

Хотя теория Калуцы – Клейна тоже была неперенормируема, живой интерес к ней пробудило то, что она давала надежду на «мраморную» теорию. Превращение уродливой, беспорядочной «деревянной» мешанины в чистую, элегантную «мраморную» геометрию было мечтой Эйнштейна. Но в 1930-е и 1940-е гг. о природе «дерева» почти ничего не знали. А к 1970 г. Стандартная модель наконец раскрыла его тайну: оказалось, что материя состоит из кварков и лептонов, связанных вместе полем Янга – Миллса и подчиняющихся симметрии SU (3) ? SU (2) ? U (1). Задача заключалась в том, как получить эти частицы и загадочные симметрии из «мрамора».

Поначалу казалось, что это невозможно. Ведь симметрии, о которых идет речь, – результат взаимообмена точечных частиц друг с другом. Если N кварков мультиплета перетасовать, получится симметрия SU (N). Она выглядит исключительно симметрией «дерева», а не «мрамора». Какое отношение SU (N) имеет к геометрии?