Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

Потребовалось немало времени, чтобы идеи Пуанкаре получили признание. Следующий прорыв произошел в 1913 году, когда Джордж Биркгоф доказал так называемую «последнюю геометрическую теорему» — недоказанное предположение, из которого Пуанкаре вывел существование, в подходящих для того условиях, периодических орбит. Мы сегодня называем этот результат теоремой Пуанкаре — Биркгофа о неподвижной точке.

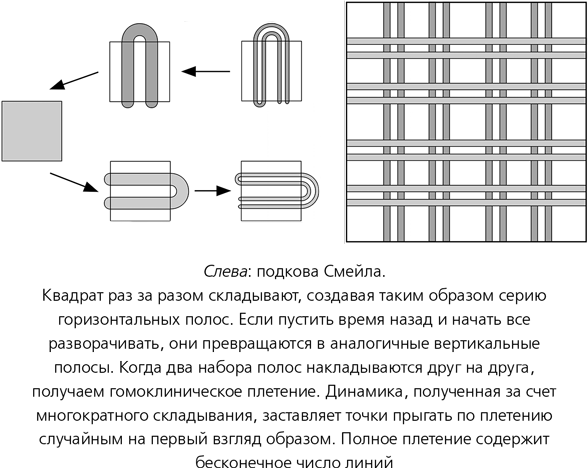
Математики и другие ученые до конца осознали существование хаоса лет 50 назад. Следуя по стопам Биркгофа, Стивен Смейл провел глубокое исследование геометрии гомоклинического плетения; он встретил ту же проблему в другой области динамики, что и побудило его заинтересоваться этим вопросом. Он придумал динамическую систему со сходной геометрией, которую намного проще анализировать; эта система получила известность как подкова Смейла. Она начинается с квадрата, который растягивается в длинный тонкий прямоугольник и загибается в форме подковы, а затем накладывается на первоначальный квадрат. Повторение этой процедуры раз за разом очень напоминает замес теста и порождает те же хаотические последствия. Геометрия подковы позволяет строго доказать, что такая система хаотична и что в некоторых отношениях она ведет себя как случайная последовательность бросков монетки, несмотря на свою полную детерминированность.

По мере того как проявлялись масштабы и богатство хаотической динамики, растущий ажиотаж в научной среде разбудил интерес к хаосу в средствах массовой информации, которые окрестили все это предприятие «теорией хаоса». На самом же деле хаотическая динамика всего лишь часть, хотя, бесспорно, значительная и захватывающе интересная часть, еще более важной области математики, известной как нелинейная динамика.