Книга: Математика космоса [Как современная наука расшифровывает Вселенную]

* * *

Должен признаться, что я придерживаю в рукаве козырь — потенциальный способ сохранить привычные законы природы и при этом полностью отказаться от темного вещества. Не потому, что ему есть экзотические альтернативы, но потому, что расчет, доказывающий вроде бы существование темного вещества, может оказаться ошибочным.

Я сказал «может оказаться» потому, что не хочу перехваливать эту идею. Но математики начинают ставить под сомнение допущения, которые входят в уравнение Кеплера, и их результаты, хоть пока и неполные, показывают, что здесь есть о чем поговорить. В 2015 году Дональд Саари проанализировал математические аргументы, при помощи которых космологи оправдывают присутствие темного вещества, и нашел свидетельства того, что законы Ньютона в теории строения галактик и кривых вращения применены неверно.

Если так, то темному веществу, вероятно, уготована судьба Вулкана.

Объектом внимания Саари является исключительно логическая структура стандартной математической модели, которую астрономы используют для вывода уравнения Кеплера. Его расчеты заставляют усомниться в том, что такая модель применима в данном случае. Это радикальная гипотеза, но Саари — специалист в математике задачи n тел и гравитации в целом, поэтому имеет смысл познакомиться с его рассуждениями. Я избавлю вас от подробных расчетов — если захочется их проверить, загляните в его статью[102].

Все опирается на уравнение Кеплера. Это уравнение следует прямо и однозначно из одного ключевого модельного допущения. Реалистичная модель галактики должна включать сотни миллиардов звезд. Их планетами и другими мелкими телами, вероятно, можно пренебречь, но точная модель представляет собой задачу n тел, где n равно 100 миллиардам или больше. Возможно, это число можно уменьшить без особого изменения результатов, но, как мы видели в главе 9, даже при n = 3 (и даже 2,5) задача n тел решается очень тяжело.

Поэтому астрономы принимают модельное допущение, которое вместе с одной элегантной математической теоремой позволяет упростить галактику до одного-единственного тела. После этого они, чтобы вывести из уравнения Кеплера теоретическую кривую вращения, анализируют движение звезды вокруг этого тела. Допущение состоит в том, что на галактических масштабах галактики больше похожи на непрерывную жидкую среду — звездный суп, чем на дискретную систему n тел. В таких условиях «непрерывной среды» применима чудесная теорема, доказанная Ньютоном. (При помощи этой теоремы он показывал, что сферические планеты можно рассматривать как точечные массы.) Суть теоремы заключается в том, что при условии некоторых разумных допущений касательно симметрии суммарная сила, действующая внутри и на некоторой сферической оболочке, равна нулю, тогда как сила, действующая вовне, в точности соответствует той, какой она была бы, если все вещество внутри оболочки было сосредоточено в центральной точке.

Представьте себе звезду в галактике — назовем ее пробной звездой — и представьте сферическую оболочку с центром в центре галактики, проходящую через эту звезду. Масса внутри этой оболочки — это то, что я чуть раньше называл «масса внутри данного радиуса». Независимо от того, как ведут себя звезды внутри оболочки, мы можем применить теорему Ньютона и сосредоточить их суммарную массу в центре галактики, при этом суммарная сила, приложенная к пробной звезде, никак не изменится. Звезды вне оболочки никакого воздействия на нее не оказывают, потому что пробная звезда лежит на этой самой оболочке. Значит, движение пробной звезды вокруг центра галактики сводится к задаче двух тел: одна звезда обращается вокруг очень тяжелой точечной массы. Уравнение Кеплера непосредственно следует из такой постановки задачи.

Допущение о симметрии, необходимое для того, чтобы можно было применять теорему Ньютона, состоит в том, что все звезды движутся по круговым орбитам и что все звезды на одинаковом расстоянии от центра галактики движутся с одинаковой скоростью, то есть динамика системы обладает вращательной симметрией. В этом случае несложно вывести точные решения уравнений движения для звездного супа. Можно выбрать либо формулу для распределения массы, либо формулу для кривой вращения, и при помощи уравнения Кеплера вывести вторую формулу. Ограничение одно: по мере роста радиуса масса должна увеличиваться.

Таким образом, модель звездного супа непротиворечива, точно согласуется с Ньютоновой гравитацией и подчиняется уравнению Кеплера. Лежащее в ее основе допущение об осевой симметрии тоже, судя по всему, не противоречит наблюдениям. Так что мы получаем освященную временем модель, основанную на умной и верной математике, и к тому же она делает задачу решаемой. Неудивительно, что астрономам она нравится.

К несчастью, в ней есть математический недостаток. Пока не ясно, насколько этот недостаток серьезен, но он определенно небезобиден и может даже оказаться фатальным.

Два аспекта этой модели вызывают вопросы. Один из них — это допущение о круговых орбитах всех звезд. Но самое серьезное — допущение о непрерывной среде (звездный суп). Проблема в том, что сглаживание распределения звезд внутри оболочки игнорирует важный аспект их динамики. А именно — эффект взаимодействия между звездами, близкими к оболочке, и той звездой, скорость обращения которой мы пытаемся вычислить.

В модели с непрерывной средой не имеет значения, вращается вещество внутри оболочки или находится в покое. Важна лишь суммарная масса внутри оболочки. Более того, сила, с которой эта масса действует на пробную звезду, всегда направлена к центру галактики. Уравнение Кеплера зависит от этих фактов.

Однако в реальной системе n тел звезды — дискретные объекты. Если вблизи пробной звезды проходит другая звезда, дискретность подразумевает, что эта проходящая звезда доминирует в местном гравитационном поле и притягивает пробную звезду к себе. Иначе говоря, проходящая звезда «тянет» пробную за собой. Это ускоряет обращение пробной звезды вокруг галактического центра. Конечно, одновременно это замедляет проходящую звезду, но ей на смену быстро приходит другая звезда, идущая непосредственно позади. Такой интуитивный аргумент позволяет предположить, что уравнение Кеплера недооценивает скорости обращения на больших расстояниях от центра. Если так, это помогает объяснить аномалию.

Вот очень упрощенная аналогия. Представьте себе маленький шариковый подшипник, приставленный сверху к вращающемуся прядильному колесу (оба находятся в одной плоскости, а гравитация отсутствует, и ничто не возмущает подшипник). Если колесо представляет собой идеально гладкую окружность, то оно никак не влияет на подшипник и может с тем же успехом покоиться. Дискретная модель n тел, однако, заменяет колесо на зубчатую шестеренку. Теперь каждый зубчик шестеренки ударяет по подшипнику, давая ему толчок в направлении вращения. С уменьшением зубчиков толчки не исчезнут, хотя и ослабнут, зато зубчиков будет больше. Так что снижение толчка за счет очень маленьких зубчиков — это не то же самое, что толчки от колеса вообще без зубчиков, которые равны нулю.

Данный аргумент нельзя воспринимать просто как неопределенные разглагольствования. Саари проводит расчеты, чтобы доказать, что сглаженный звездный суп не в состоянии адекватно моделировать распределение n тел для большого n. В частности, в нем не учитывается эффект «буксировки». Однако в целом этот эффект может оказаться невелик, поскольку реальная динамика n тел сложнее, чем только что приведенный сценарий. Чтобы оценить важность эффекта буксировки, нам придется использовать точную модель системы n тел для всех звезд внутри оболочки и найти с ее помощью их суммарное действие на пробную звезду.

Лучший способ сделать это состоит в том, чтобы построить такое состояние системы n тел, которое сохранит все ключевые свойства, предполагаемые у звездного супа, за исключением непрерывности. Если данное конкретное состояние изменяет уравнение Кеплера, мы можем быть практически уверены, что причина как раз в том, что n дискретных тел заменены непрерывным звездным супом. Эти ключевые свойства — симметричное распределение масс, при котором каждая звезда движется по окружности, и ее ускорение направлено к центру галактики.

Хотя в общем случае мы не можем записать в явном виде решения задачи n тел, существует один класс решений, для которых это может быть сделано, известный как центральные конфигурации. В этих особых состояниях концентрические круги звезд, напоминающие паутину, все вращаются с одной и той же угловой скоростью, как если бы конфигурация была жесткой. Эта идея восходит к работе Джеймса Кларка Максвелла 1859 года о стабильности колец Сатурна, упомянутой в главе 6 в качестве доказательства того, что кольца не могут быть сплошными и твердыми. Саари использует аналогичную идею, чтобы показать, что звездный суп не в состоянии правильно моделировать галактическую динамику.

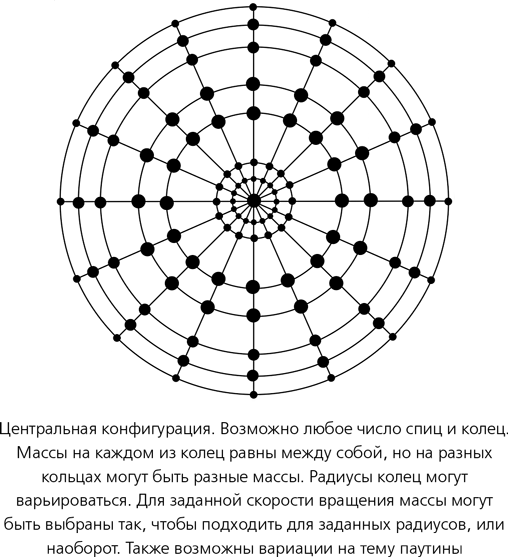
Центральные конфигурации искусственны в том смысле, что никто не станет ожидать такой правильной формы от реальной галактики. С другой стороны, это разумный выбор для исследования того, как сочетаются непрерывная среда и модель n тел. Если выбрать в паутине достаточно радиальных линий и достаточно окружностей, мы получим очень плотный звездный суп, который хорошо аппроксимируется непрерывной средой. Паутинная конфигурация тоже удовлетворяет, с очень хорошим приближением, условиям симметричности, использованным при выводе уравнения Кеплера. Так что аппроксимация типа «звездный суп» должна, по идее, работать.

В частности, для вращающейся паутины должно выполняться уравнение Кеплера. Мы можем это проверить, использовав тот вариант, в котором распределение массы выражается через скорость на заданном радиусе. Поскольку паутина вращается жестко, скорость пропорциональна радиусу. Таким образом, уравнение Кеплера предсказывает распределение масс, пропорциональное кубу радиуса. Такой результат сохраняется, какими бы ни были на самом деле массы звезд в конфигурации.

Чтобы это проверить, мы проведем точный дискретный расчет n тел для паутины. Теория центральных конфигураций допускает значительную гибкость в выборе масс звезд. К примеру, если каждая звезда (а следовательно, каждое кольцо) обладает одинаковой массой, центральные конфигурации существуют, и распределение массы вдоль радиуса всегда меньше чем константа, умноженная на радиус. В данном случае, однако, из уравнения Кеплера может следовать, что масса самого далекого внешнего кольца в миллион раз больше массы внутреннего, даже в том случае, когда на самом деле их массы одинаковы. Так что точные расчеты не оправдывают упрощенную модель, из которой получено уравнение Кеплера. Напротив, по мере увеличения радиуса правильно вычисленная масса растет намного медленнее, чем предсказывает формула Кеплера.

Этот расчет доказывает, что модель в варианте звездного супа может дать результат со значительной ошибкой, даже когда предположения, на которых модель основана, выполняются. Несмотря на популярное выражение, отражающее бытовой, житейский взгляд на вещи, одного исключения достаточно, чтобы опровергнуть любое правило[103].

Расчеты Саари имеют еще одно важное следствие. Если темное вещество, как считают астрономы, существует и образует вокруг галактик обширные, массивные гало, то оно не может на самом деле объяснить аномальную кривую вращения, с которой, собственно, все и началось. Либо закон всемирного тяготения, либо традиционные модельные допущения должны быть неверны.