Книга: Кому мешает ДНК-генеалогия?

Глава 4 Расчетные методы ДНК-генеалогии. Константы скоростей мутаций в маркерах и в гаплотипах

Глава 4

Расчетные методы ДНК-генеалогии. Константы скоростей мутаций в маркерах и в гаплотипах

Это – центральный вопрос ДНК-генеалогии, и мы уделим этому особое внимание. Вопросов в этом отношении задается много, что вызвано тремя основными причинами: (1) относительная сложность вопроса, (2) неупорядоченный, статистический характер мутаций, при котором число мутаций при относительно малом числе маркеров и за относительно малый промежуток времени является нестабильным, и для неопытного человека представляется принципиально невоспроизводимым, и (3) крайняя запутанность популяционными генетиками этой темы на протяжении последних 20 лет.

Вопрос 60: С какими скоростями происходят мутации в гаплотипах?

Выше (в ответе на Вопрос 14) было показано, что в маркере DYS393 значение аллели 13 сохраняется во всех трех рассмотренных гаплотипах (русского и двух киргизов), отделенных друг от друга тысячелетиями, а в маркере DYS390 за то же время мутация произошла дважды, и все три аллели оказались разными – 24, 25 и 26. Три гаплотипа в данном случае не очень показательны, статистика не та, но в целом так и должно быть, потому что константа скорости мутации в маркере DYS393 равна 0.00059 мутаций на условное поколение (25 лет), а в маркере DYS390 – почти в четыре раза выше, 0.0022 мутаций на условное поколение.

Что эти числа реально означают?

Они означают, что в маркере DYS393 мутация происходит в среднем раз в 1/0.00059 = примерно 1700 условных поколений, то есть раз в 42 500 лет. В трех независимых маркерах DYS393 мутация в среднем проходит примерно раз в 14 тысяч лет. А общий предок всех трех гаплотипов в примере выше жил примерно 5 тысяч лет назад, поэтому мутация и не успела произойти, все три аллели равнялись 13, то есть показывали 13 тандемных повторов. В маркере DYS390 мутация происходит в среднем раз в 1/0.0022 = 455 условных поколений, то есть примерно раз в 11 тысяч лет, то есть для трех независимых маркеров мутация в среднем произойдет раз в 3800 лет (округлено). Вот она и произошла, и даже дважды за 5 тысяч лет. Естественно, здесь это только полуколичественные расчеты, потому что три маркера – это не статистика, но здесь показан принцип расчета. Если бы у нас было в наличии тысяча гаплотипов, расчеты были бы намного точнее. В таком случае в тысяче маркеров DYS393 за пять тысяч лет (200 условных поколений) было бы 1000х0.00059х200 = 118 мутаций, а в маркере DYS390 было бы 1000х0.0022х200 = 440 мутаций. С такой статистикой уже можно работать.

Давайте посмотрим, что наблюдается в более протяженных сериях гаплотипов. Взглянем на серию из 3466 гаплотипов гаплогруппы R1b-L21. Число аллелей в маркере DYS393:

11 – 2 (то есть аллель 11 встречается в 3466 гаплотипах всего два раза)

12 – 81

13 – 3237

14 – 145

15 – 1

Считая, что все мутации одношаговые, получаем 232 мутации на 3466 аллелей – от базового значения аллели, равного 13, то есть в среднем 0.067 мутаций на маркер DYS393. Как проводятся поправки на возвратные мутации в таких системах мы рассмотрим в следующем разделе. Такие поправки нужны, потому что часть мутированных маркеров не только продолжают мутировать, уходя все дальше от предковой аллели (например, 13 ? 14 ? 15, или 13 ? 12 ? 11), но по тем же законам статистики возвращаются в исходное положение (13 ? 14 ? 13, 13 ? 12 ? 13), и потому мы часть мутаций недосчитываем.

Для другого примера возьмем не «медленный» маркер, как DYS393, а «быстрый», например, DYS390, из той же серии в 3466 гаплотипов субклада R1b-L21. Число аллелей в маркере DYS390:

21 – 3

22 – 22

23 – 228

24 – 2364

25 – 815

26 – 33

27 – 1

Видно, что мутации уже более «размазанные» по аллелям. Считая, что все мутации одношаговые, получаем 1165 мутаций на 3466 аллелей, то есть в среднем 0.336 мутаций на маркер DYS390. Мы видим, что среднее число мутаций в маркере DYS390 для той же серии гаплотипов уже в пять раз выше. Если бы не сложности статистического характера, упомянутые выше, можно было бы полагать, что эта разница отражает количественную разницу в соответствующих константах скорости мутации для маркеров DYS393 и DYS390, но это не совсем так. Константы равны 0.00059 и 0.0022 мутаций на маркер на условное поколение, то есть различаются только в 3.7 раз. Под «сложностями статистического характера» здесь понимаются и введение поправок на возвратные мутации, и несимметричность распределения числа мутаций «вверх» и «вниз» (см. приведенные выше примеры), и наличие нижестоящих субкладов, гаплотипы которых могут (системно) по мутациям отличаться от гаплотипов вышестоящих субкладов, и многие факторы, которые надо учитывать при корректном анализе в ДНК-генеалогии. Примеры даны ниже.

Вопрос 61: Что такое поправки на возвратные мутации, и как они рассчитываются?

Как было пояснено выше, вклад возвратных мутаций вызывается тем, что часть мутаций вернулись в исходное положение предковой аллели (13 или 24 для случаев маркеров DYS393 и DYS390, рассмотренных выше), и таким образом мы наблюдаем некоторый недобор мутаций. Формулы для расчетов поправочных коэффициентов даны в работах[57], и в простейшем виде симметричной картины мутаций формула следующая:

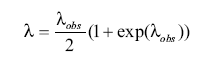
где:

?_obs = наблюдаемое среднее число мутаций на маркер в рассматриваемой серии гаплотипов,

? = среднее число мутаций на маркер, с учетом поправки на возвратные мутации.

В примере с DYS393, рассмотренном выше, поправка будет минимальной, поскольку маркер «медленный», и мутаций наблюдается мало, как в «одну», так и в «другую» сторону от исходного положения аллели. Тем не менее, рассчитаем этот поправочный коэффициент, для иллюстрации. Поскольку наблюдаемое среднее число мутаций на маркер равно 0.067, поправочный коэффициент равен 1.0345, и полная запись расчета следующая:

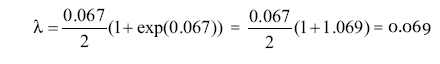
(1+1.069)/2 = 1.0345

Итак, мы наблюдаем 0.067 мутаций на маркер, а на самом деле их 0.069 мутаций на маркер, то есть всего на 3 % больше. Те мутации, что мы теряем, вернулись в исходное положение, и не учитываются при «линейных» подсчетах.

В примере c маркером DYS390, также рассмотренном выше, поправка будет значительной, поскольку маркер «быстрый», и мутаций наблюдается много, как «вверх», так и «вниз» от исходного положения аллели. Рассчитаем этот поправочный коэффициент. Поскольку наблюдаемое среднее число мутаций на маркер равно 0.336, получаем, что поправочный коэффициент равен 1.1997, и полная запись

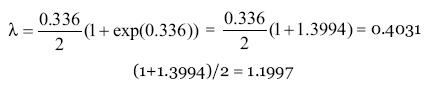
Итак, мы наблюдаем 0.336 мутаций на маркер, а на самом деле их 0.403 мутаций на маркер, то есть 20 % больше. Те мутации, что мы теряем, вернулись в исходное положение, и не учитываются при «линейных» подсчетах.

Вопрос 62: Насколько точны (или неточны) расчеты в ДНК-генеалогии? – продолжение Вопроса 32.

В сети довольно часто встречаются сомнения в отношении расчетов в ДНК-генеалогии, например, в таком виде (вопрос взят с международного форума DNA Rootsweb, перевод с английского):

? Есть фундаментальная проблема с «научными» расчетами времен жизни общего предка, где расчеты, основаны на частотах встречаемости мутаций разных маркеров. Эти частоты – просто оценки, основанные на встречаемости мутаций в современных гаплотипах. Но когда я смотрю на гаплотипы людей, общий предок которых известен и жил 400–500 лет назад, и я не вижу в их гаплотипах никаких мутаций, то у меня возникают резонные сомнения о надежности расчетов, основанных на мутациях.

Ну что здесь сказать? Когда человек не имеет понятия о том, о чем говорит, и «выходит на публику с сомнениями», когда рассуждают «по понятиям», где надо «по науке», то там может помочь только методичное просвещение. Например, следующее.

Если этот «критик» говорит о 6-маркерных гаплотипах, то там одна мутация образуется в среднем раз в 1/0.0074 = 135 условных поколений, то есть раз в 135х25 = 3375 лет. Если речь о 12-маркерных гаплотипах, то там одна мутация образуется в среднем раз в 1/0.02 = 50 условных поколений, то есть раз в 50х25 = 1250 лет. Если – о 37-маркерных гаплотипах, то там одна мутация образуется в среднем раз в 1/0.09 = 11 условных поколений, то есть раз в 11х25 = 275 лет. Но в среднем – это не обязательно точно раз в 275 лет, как часы. Это может быть мутация через 100 лет, и через 600 лет, и как угодно, но при большом числе гаплотипов это получается в среднем раз в 275 лет. Поэтому критик не понимает того, что просто «гаплотипов» в таких случаях писать нельзя, надо обязательно указывать, какой протяженности гаплотипы. Как мы видим, и в случае 37-маркерных гаплотипов вполне возможно, что за 400–500 лет в них не происходит мутации. Но если речь о 111-маркерных гаплотипах, в которых мутация происходит в среднем раз в 125 лет, то за промежуток времени 400–500 лет мутации должны наблюдаться. Хотя и при бросании монеты бывает, что орел или решка выпадают подряд 4–5, и даже 6 раз. Хотя в среднем выпадают каждый второй раз.

Поэтому принцип должен быть такой, что при рассмотрении и обсуждении мутаций надо всегда исходить из вероятностного характера процесса.

Вообще при обсуждении вопроса в понятиях «точны» или «неточны», надо сначала определиться, «точны» для чего, для какой задачи, которая должна ставиться. Если задача ставится вычислить время рождения или смерти общего предка с точностью до года, то никакие статистические методы для этого в принципе не подходят, включая ДНК-генеалогию. Не подходят и задачи, в которых требуются проводить расчеты с точностью до десятилетий. ДНК-генеалогия решает задачи в первую очередь концептуальные, на уровне открытий, пересмотров старых концепций, и создания концепций новых. Никто же не требует в астрофизике расчета времени «большого взрыва» Вселенной с точностью до сотен лет, и тем более до года, там оценки идут на сотни миллионов и миллиарды лет, и не в сотне лет точности была важность новой концепции.

Например, когда 20 лет назад популяционными генетиками было сообщено, что носители гаплогруппы R1b жили в Европе 30 тысяч лет назад, во времена неандертальцев, то расчетов вообще никаких не делалось, это было предложено «по понятиям», подхвачено, и устоялось в науке. Потребовалось больших трудов убедить научную общественность, что R1b появились в Европе всего лишь около 5000 лет назад, как показали расчеты ДНК-генеалогии[58], и это имело концептуальную значимость. В той ситуации было неважно, это 5000±3000 лет назад, 5000±1000 лет назад, или 4800±400 лет назад (последняя величина была показана в расчетах). Таких примеров можно привести много, и каждый раз это был фактический прорыв в науке, прорыв разного масштаба.

Обычно расчеты общих предков выборок в ДНК-генеалогии проводятся с точностью 10–15 %, и причина этого довольно проста – мы постулируем, что величина константы скорости мутации определяется с точностью ±10 %, и тогда точность расчетов по определению не может быть лучше, чем ±10 %. На самом деле сотни и тысячи расчетов показали, что точность определения констант скоростей мутаций составляет примерно 2.5–3.0 %, но для расчетов мы оставляем те же 10 %. Лучше пусть доверительный интервал расчетов будет больше, чем претендовать, что наши расчеты точны, и время от времени подвергаться обвинениям, что другие данные показывают несколько отличающуюся величину. Не все знают, что расчеты погрешностей дело весьма условное, и зависит от закладываемых параметров доверительности. Если мы хотим результаты с доверительностью 95 %, или 99 %, то погрешности при тех же исходных величинах будут уже другими. В ДНК-генеалогии неразумно считать с требуемой доверительностью 95 % или 99 %, потому что тогда мы выходим уже не на концептуальность, а на точность, которой в обычно используемых сериях гаплотипах нет и быть не может. Даже если выборки будут состоять из десятков и сотен тысяч протяженных гаплотипов, в них непременно окажутся «примесные» гаплотипы, из других субкладов, из несимметричных ДНК-линий, да и просто ошибки типирования, которые неизбежны в больших сериях.

Поэтому реальность показывает, что погрешности расчетов ±10 %-15 % это то, из чего надо исходить и соответственно формулировать требования и задачи исследования.

В качестве примеров осложняющих факторов рассмотрим приведенные выше распределения мутаций в маркерах DYS393 и DYS390 в серии из 3466 гаплотипов субклада R1b-L21. Как мы видели, в обоих случаях мутации дают несимметричную картину. В DYS393 – в одну сторону, на понижение аллелей, произошло 85 одношаговых мутаций, в другую, на повышение, произошло 147 мутаций. На самом деле это не мутации несимметричные, а несимметричное распределение потомков по мутациям. Например, среди тех 3466 человек рассматриваемой серии оказалось больше потомков с DYS393 = 14, чем с DYS393 = 12. Причин к такому несимметричному распределению мутаций много. Например, среди всей серии из 3466 гаплотипов могло оказаться непропорционально много потомков того, у кого много веков назад произошла мутация DYS393 = 13 ? 14. Далее, в число этих 3466 человек могли попасть обладатели подчиненных (или вообще других) субкладов, с преобладанием базовой аллели, DYS393 = 14. Если в данную серию попали носители других субкладов с другой базовой аллелью, то такая несимметричность несколько искажает результаты расчетов, как мы покажем ниже на нескольких характерных примерах, и потому результаты расчетов времени до общего предка всегда должны даваться с определенной погрешностью, которая перекрывает искажения. Если это «свои» потомки, то результаты расчетов обычно не искажаются. Этот вопрос пока недостаточно проработан в ДНК-генеалогии с теоретической точки зрения.

В маркере DYS390 в той же серии гаплотипов субклада R1b-L21 мутации тоже дают несимметричную картину. В одну сторону, на понижение аллели на одну единицу, произошло 228 мутаций, в другую, на повышение, произошло 815 мутаций, и в целом на понижение аллелей произошло 281 одношаговый мутаций и на повышение – 884 одношаговых мутаций. Причины несимметричности могут быть те же, что описаны выше. Надо отметить, что в этих двух примерах случайно получилось, что на повышение прошло больше мутаций, чем на понижение, но есть множество обратных примеров, например для того же маркера DYS393 в серии из 269 гаплотипов гаплогруппы N1c1 на понижение произошло больше мутаций (но по сути мутации были почти симметричными). Число аллелей в маркере DYS393:

13 – 12 (то есть аллель 13 встречается в 269 гаплотипах 12 раз)

14 – 248

15 – 8

16 – 1

Всего среди 269 маркеров DYS393 в данной серии суммарно произошло 22 одношаговых мутаций (12 «вниз» и 10 «вверх»), и зная, что константа скорости мутации в маркере DYS393 равна 0.00059 (это было определено по множеству серий гаплотипов разных гаплогрупп), мы можем примерно расчитать, когда жил общий предок рассмотренной серии гаплотипов группы N101 (строго говоря, серии маркеров DYS393):

22/269 = 139 условных поколений назад, то есть примерно 139х25 = 3475±740 лет назад (при стандартном расчете погрешности). Действительно, расчеты по гаплотипам разной протяженности дали время жизни общего предка данной выборки из 269 гаплотипов 3233±326 лет назад (111-маркерные гаплотипы), 3287±333 лет назад (67-маркерные гаплотипы), 346±353 лет назад (37-маркерные гаплотипы), 4127±424 лет назад (25-маркерные гаплотипы). Здесь мы расчеты умышленно не округляем, чтобы не вносить произвол при сопоставлении серии результатов. Мы видим, что расчеты даже по одному маркеру дали вполне приемлемую величину времени до общего предка данной серии гаплотипов. Возможно, это потому, что серия мутаций в данном маркере вполне симметричная.

Если мы посмотрим на DYS390 c его средней величиной числа мутаций на маркер в серии из 3466 гаплотипов субклада R1b-L21, равной 0.4031 (после введения поправки на возвратные мутации), то получим 0.4031/0.0022 = 183 условных поколений, или примерно 4580 лет со времени жизни общего предка субклада R1b-L21. Заметим, что по данным компании YFull (http://www.yfull.com/tree/R1b/) субклад L21 образовался 4500±300 лет назад. Правда, расчет по всем 111 маркерам для 3466 гаплотипов субклада L21 показал, что общий предок современных носителей этого субклада жил 3810±381 лет назад. Это приходится на границу диапазона погрешности расчетов, но в принципе результаты расчетов в их совокупности и в совокупности с данными других независимых расчетов показывают, что общий предок современных носителей субклада R1b-L21 жил действительно на несколько сотен лет позже времени образования самого субклада; потомство от более ранних предков не выжило.

Пример того, что во многих случаях несимметричность в распределении мутаций в маркерах выражается в том, что на повышение проходит меньше мутаций, чем на понижение (то есть обратно тому, что наблюдается в маркере DYS390 в серии гаплотипов субклада R1b-L21), является серия из 4769 гаплотипов гаплогруппы R1a. Там число аллелей в маркере DYS390 выглядит следующим образом:

22 – 5

23 – 66

24 – 755

25 – 3544

26 – 383

27 – 16

Считая, что все мутации одношаговые, находим, что в 4769 маркерах DYS390 прошло 1317 мутаций, получаем, что среднее число мутаций на маркер равно 0.276. Это число не является корректным, потому что мы знаем, что среди тех 4769 гаплотипов было множество, относящихся к разным субкладам, каждый из которых имеет разную историю и своих общих предков. Поэтому любые расчеты с этими числами будут являться «поверхностными», очень приблизительными. Задача ДНК-генеалогии – проводить «рассечения» серий гаплотипов на ветви, семейства, группы, и при соответствующей поставленной задаче проводить их отдельные и независимые рассмотрения.

Подобные расчеты по всем 111 маркерам (или тому числу маркеров, которое было выбрано для рассматриваемых гаплотипов) после усреднения дает «возраст» общего предка рассматриваемой выборки гаплотипов, при условии, что общий предок был один, согласно соответствующим критериям ДНК-генеалогии.

Не нужно думать, что все 111 маркеров дадут одну и ту же величину «возраста» до общего предка, например, как 4580 лет в случае маркера DYS390 в серии гаплотипов субклада R1b-L21. Как раз в данном конкретном случае датировка маркера оказалась несколько завышенной из-за несимметричности распределения мутаций. Но по одному маркеру никогда возраст до общего предка не считают. В данном случае для 3466 гаплотипов в 111 маркерном формате для статистических расчетов суммарно имеются 384728 аллелей, причем расчет с применением калькулятора Килина-Клёсова (см. ниже) ведется и по каждому из маркеров, «по вертикали», и по всем мутациям по всем гаплотипам, «по горизонтали», как по «квадратичному» методу, в котором поправки на возвратные мутации уже учтены, так и «линейным методом», с введением поправок на возвратные мутации, а также и по разным длинам гаплотипов. В итоге калькулятор выдает результат по каждому варианту расчета, так что можно сравнивать и смотреть, нет ли систематических отклонений. В данном случае, по 3466 гаплотипам, получилось (лет до общего предка субклада R1b-L21):

3810±381 по 111-маркерным гаплотипам, линейный метод

4197±274 по 111-маркерным гаплотипам, квадратичный метод

3841±384 по 67-маркерным гаплотипам, линейный метод

3576±358 по 37-маркерным гаплотипам, линейный метод

3571±358 по 25-маркерным гаплотипам, линейный метод

3679±369 по 17-маркерным гаплотипам, линейный метод

3499±352 по 12-маркерным гаплотипам, линейный метод

4161±421 по 6-маркерным гаплотипам, линейный метод

Как видим, расчеты дали вполне удовлетворительное совпадение в пределах погрешности измерений, даже для коротких 12– и 6-маркерных гаплотипов.

Человек сторонний, не очень знакомый со статистикой, скажет – как же так, расчеты по одному маркеру, DYS390, дали примерно 4580 лет со времени жизни общего предка субклада R1b-L21, а расчеты по всем 111-маркерным гаплотипам, с общим числом аллелей 384728, дали 3810±381 или 4197±274 лет, по линейному и квадратичному методам, то есть заметно ниже. Но в этом статистика и заключается, что мутации неупорядоченные, по отдельности различаются, но все они группируются вокруг некого «центра», «ядра», и при усреднении математический аппарат дает среднюю величину и величину погрешности расчетов, или среднее квадратичное отклонение при определенных доверительных интервалах. В данном случае DYS390 – это всего один маркер, а их сто одиннадцать. Но даже в 6-маркерных гаплотипах, куда DYS390 входит, усреднение по всем шести дает датировку 4161±421 лет, то есть датировка по одному DYS390 входит в диапазон погрешностей. А датировка по 6-маркерному гаплотипу входит в диапазон погрешностей для серии 111-маркерных гаплотипов.

Вопрос 63: Как проводились расчеты констант индивидуальных скоростей мутаций для всех 111 маркеров?

Это – результат большой работы, которая проводилась с 24 сериями 111-маркерных гаплотипов практически всех гаплогрупп, для которых в базах данных эти гаплотипы были числом хотя бы в несколько десятков. Для большинства гаплогрупп расчетные серии содержали сотни гаплотипов – помимо упомянутых ранее 3466 гаплотипов субклада R1b-L21, были 859 и 976 111-маркерных гаплотипов гаплогруппы R1a (разные серии), 829 гаплотипов гаплогруппы R1b-Uio6, 968 гаплотипов гаплогруппы I1, 661 гаплотипов гаплогруппы J, 1417 гаплотипов гаплогруппы J2, и так далее, общим числом П850 гаплотипов в 111-маркерном формате. При этом проверялась сходимость расчетов гаплотипов разных форматов и расчетов разными методами. Результаты этой работы опубликованы в Вестнике Академии ДНК-генеалогии в 2015 году[59].

Расчеты констант скоростей мутаций в маркерах производятся на основании их распределений в больших сериях гаплотипов. Чем меньше константа скорости мутации данного маркера, тем, естественно, меньше мутаций за определенное время, в качестве которого обычно рассматривается время, прошедшее от общего предка. Если взять, например, серию из 3466 гаплотипов субклада R1b-L21, к которой мы здесь неоднократно обращались именно потому, что она одна из наиболее репрезентативных по численности гаплотипов, то маркере DYS472 там всего пять мутаций:

7 – 1 (то есть аллель 7 встречается в 3466 маркерах DYS472 всего один раз)

8 – 3461 раз

9 – 4 раз

В маркере DYS393 в той же серии уже 232 мутации:

11 – 2

12 – 81

13 – 3237

14 – 145

15 – 1

В маркере DYS390 – 1165 мутаций:

21 – 3

22 – 22

23 – 228

24 – 2364

25 – 815

26 – 33

27 – 1

Поскольку время от общего предка во всех трех случаях одно и то же, то даже не зная его, уже можно заключить, что константы скорости мутаций должны отличаться друг от друга в пропорции 5: 232: 1165 (числа – количества мутаций от базового маркера для трех маркеров), или, пропорционально, 1: 46: 233 Это – тогда, когда нет осложняющих факторов, которые, впрочем, есть всегда. Среди этих факторов – примесь посторонних гаплотипов, почти неизбежная при массовых тестированиях, перекошенная серия гаплотипов, когда одних родственников (даже отдаленных) в серии больше, чем других, когда в серии присутствуют представители нижестоящих субкладов, причем одних субкладов больше, чем других, и так далее. Вывод такой, что одной серией гаплотипов при расчетах констант скоростей мутаций ограничиваться нельзя, надо проводить рассмотрение многих серий гаплотипов из разных гаплогрупп, выяснять по возможности причины различий, и усреднять полученные константы скоростей мутаций по разным сериям. В некоторых сериях отклонения буквально гипертрофированные – например, в той же серии R1b-L21 оказалось несколько сотен гаплотипов дочернего субклада R1b-M222, у которого характерная величина аллели DYS392=14 вместо обычной DYS392=13. Если этого не знать или не заметить, то число мутаций в медленном маркере DYS392 окажется завышенным на сотни мутаций, и формально рассчитанная «константа скорости» окажется несуразно высокой.

При сопоставлении расчетных констант по большой серии гаплогрупп такие искажения должны быть заметны, проанализированы, и если причина выяснена и действительно показано, что это искажения, то эти выпадающие величины должны быть приняты во внимание. Таким образом видно, что это кропотливая и большая работа. Дилетанты или прочие любители обычно выхватывают одну серию гаплотипов, делят одно на другое, без всяких перекрестных проверок и размышлений, и вуаля, ответ готов. Он часто такой – «расчеты по мутациям смысла не имеют». Пример такой дилетантской (в данном отношении) статьи Busby et al (2011)[60], сюда же относятся неквалифицированные рассуждения Dienekes Pontikos[61], и прочих. Они основывались именно на выхватывании отдельных величин, которые оказались искаженными, и отсюда делались «глобальные» негативные выводы. По аналогии, можно бросить монету три раза, и на основании полученного результата объявить теорию вероятности «псевдонаукой».

Проще с протяженными гаплотипами, в первую очередь 67– и 111-маркерными, в которых искажения в индивидуальных маркерах, которые (искажения) также имеют статистический характер, уравновешиваются, компенсируются на множестве маркеров, и в итоге дают взаимно согласованные данные. Примеры (показаны датировки протяженных серий 111-маркерных гаплотипов, первая колонка – 67-маркерные гаплотипы, вторая – 111-маркерные), датировки без округления:

Часто спрашивают, а сохраняются ли константы скоростей мутаций в других гаплогруппах и субкладах? Ответ – естественно, сохраняются, так как откуда, например, маркер DYS393 «знает», какая там снип-мутация имеется на другом конце Y-хромосомы, и которая определяет носителя Y-хромосомы в определенный субклад? Маркер есть маркер, это обычно три– или тетра-нуклеотид, повторяющийся определенное количество раз в Y-хромосоме. Раз в несколько тысяч лет он удлиняется или укорачивается на одно (обычно) звено, и что ему до удаленной снип-мутации? Но люди интересуются, обычно не задумываясь о таких деталях, им представляется, что гаплогруппа – это что-то большое и материальное, вляющее на скорости мутации во всей Y-хромосоме каким-то чудодейственным образом.

Еще пример – субклад R1b-M222, в котором 818 аллелей маркера DYS393 распределяются следующим образом:

12 – 5

13 – 791

14 – 22

Число мутаций (от базового значения маркера) равно 27, что дает 27/818/0.00059 = 56 ? 57 условных поколений, или 1425±310 лет до общего предка. По данным расчета по снипам субклад R1b-M222 образовался 4300 лет назад (http://www.yfull. com/tree/R1b/), но популяция прошла бутылочное горлышко, и общий предок современных носителей R1b-M222 жил на три тысячи лет позже. Такое бывало довольно часто.

Еще один непростой пример – гаплогруппа J2. Пример непростой, потому что гаплогруппа древняя, и состоит из многих обрывков ДНК-генеалогических линий, которые усложняют расчеты. Посмотрим, насколько однородный там набор из 587 аллелей маркера DYS393, которые распределяются следующим образом:

9 – 1

10 – 0

11 – 5

12 – 510

13 – 65

14 – 5

15 – 1

Всего – 86 одношаговых мутаций. Мы видим опять несимметричное распределение аллелей, идущих «на понижение» и «на повышение». Но если это пока отложить на последующее рассмотрение, то 86 мутаций для 587 аллелей – это при равном «возрасте» общего предка соответствует 508 мутациям для 3466 аллелям (в субкладе R1b-L21), а там – только 232 мутации, то есть в 2.19 раз меньше. В идеальном случае (без осложняющих факторов) это соответствует датировке общего предка для выборки J2 примерно 3810x2.19 = 8300 лет. Определение датировки по 417 гаплотипам (другая выборка) гаплогруппы J2 дало 8993±903 и 9914±993 лет до общего предка (по 67– и 111-маркерным гаплотипам). Разница заметная (8 % и 19 %, соответственно), но район датировок тот же, тем более с учетом, что мы сравниваем датировку по одному маркеру с датировками по 67 и 111 маркерам.

Еще одна илюстрация, как примеси сторонних субкладов искажают датировки. В субкладе R1b-L21 3466 аллелей DYS392 распределяются следующим образом:

11 – 8

12 – 22

13 – 2715

14 – 675

15 – 30

16 – 16

Здесь перекос в распределении (по маркеру DYS392=14) вызван тем, что подавляющая часть аллелей «14» относится к нижестоящему субкладу R1b-M222, в котором данная аллель является предковой, и закрепилась в последующих поколениях. В итоге из 821 мутаций 675 относится к отдельному субкладу, со своим общим предком. Для правильного расчета надо инородные аллели снимать, например, путем построения дерева гаплотипов, в котором субклад М222 уйдет в отдельную ветвь, и соответствующие гаплотипы из счета надо также снимать. При этом снятыми окажутся 655 аллелей «14», 24 аллели «15» и все 16 аллелей «16», и распределение окажется вполне симметричным:

11 – 8

12 – 22

13 – 2715

14 – 19

15 – 5

Вопрос 64: Как связаны между собой индивидуальные константы скорости отдельных маркеров, и суммарная (кумулятивная) константа скорости мутации по всему гаплотипу?

Выше мы рассматривали константы скоростей мутаций в отдельных маркерах, как 0.00059 мутаций на условное поколение в маркере DYS393, или 0.00220 мутаций на условное поколение в маркере DYS390. И здесь вступает в силу важное правило химической кинетики: константы скоростей в параллельных реакциях (в данном случае – мутациях) суммируются, если регистрируется расходование исходного вещества или образование суммарного продукта реакции, и изучается скорость этого суммарного процесса. Простой пример – если из бассейна вода вытекает по нескольким трубам разной толщины, то можно изучать скорость вытекания воды по каждой трубе отдельно, но если интересует общая потеря воды, то суммируется потеря воды по всем трубам. Это практически полная аналогия с расходованием предкового гаплотипа и с накоплением гаплотипов потомков. Этот процесс можно изучать по каждому маркеру в отдельности, а можно – по всему гаплотипу, то есть по сумме маркеров.

Рассмотрим простой случай – 12-маркерный гаплотип, состоящий из маркеров DYS 393, 390, 19, 391, 385a, 385b, 426, 388, 439, 389-1, 392, 389-2. Пример – гаплотип гаплогруппы I2a, а именно ее ветви L147.2, к которой относятся почти все восточноевропейские носители этой гаплогруппы, общий предок которых жил примерно 2300 лет назад:

13 24 16 11 14 15 11 13 13 13 11 31

Константы скоростей индивидуальных маркеров следующие:

DYS393 0.00059

DYS390 0.00220

DYS19 0.00179

DYS391 0.00220

DYS385a 0.00280

DYS385a 0.00360

DYS426 0.00009

DYS388 0.00022

DYS439 0.00300

DYS389-1 0.00080

DYS392 0.00040

DYS389-2 0.00231

Но поскольку мутации во всех этих маркерах происходят независимо и неупорядоченно, и мы, как правило, заинтересованы в скорости мутации всего гаплотипа, а не его отдельных маркеров (многочисленные примеры будут даны ниже), то суммарная константа скорости мутаций во всем гаплотипе равна сумме индивидуальных констант скоростей, которая равна 0.0200 мутаций на условное поколение (25 лет).

Так же рассчитываются суммарные константы скорости мутаций в гаплотипах, которые приведены ниже.

Надо сказать, что здесь даются упрощенные примеры, потому что по двум гаплотипам расчеты обычно не ведут, ведут по десяткам, сотням и тысячам гаплотипов, если таковые есть в наличии, рассчитывают математические погрешности в определяемых числах, и т. д. В таких случаях погрешности расчетов приближаются к плюс-минус 10 % от определяемой величины, поскольку именно такой определена погрешность вычисления константы скорости мутации. Здесь только иллюстрируется принцип расчета.

Ясно, что у протяженных 111-маркерных гаплотипов разрешение лучше (400-маркерные гаплотипы пока крайняя редкость). Но их определять дороже, чем более короткие, поэтому в академических исследованиях, при постоянной нехватке денежных средств, приходится работать с более короткими гаплотипами. Протяженные гаплотипы определяют в коммерческих компаниях, обычно персонально, каждый для себя, и передают, как правило, в общественные базы данных. Сейчас в общественных базах данных – сотни тысяч гаплотипов, и базы прирастают многими гаплотипами ежедневно[62].

Вопрос 65: Какие значения имеют все 111 маркеров, применяемые в ДНК-генеалогии?

Таблица приведена ниже. Числа 0.02, 0.046 и 0.09 справа – значения констант скоростей мутаций для 12-, 25-, и 37-маркерных гаплотипов, выраженных в мутациях на гаплотип на условное поколение (в 25 лет). Для 67-маркерных гаплотипов, которые заканчиваются маркером DYS565 константа скорости равна 0.12 мутаций на гаплотип на условное поколение. Самое последнее число, 0.198 – константа скорости мутаций на 111-маркерный гаплотип на условное поколение. Эти величины приведены и обоснованы в статье[63] Клёсова и Килина (2015). Обоснование велось по восьми направлениям:

1) Сопоставление датировок, полученных с помощью линейного метода (ЛМ) по 67– и 111-маркерным гаплотипам. Это – наиболее достоверные форматы гаплотипов.

2) Сопоставление датировок, полученных с помощью ЛМ по п.1, и 37-, 25-, 17-, 12 и 6 – маркерным гаплотипам. При этом надо принимать во внимание, что чем меньше число маркеров, тем выше разброс. Поэтому разброс – это нормально, но систематическое (или постоянное) завышение или занижение результатов по сравнению с 67/111 маркерными расчетами – это ненормально. В каждом случае причины соответствующих отклонений анализировались.

3) ЛМ по п.1 и 22-маркерным (медленным) гаплотипам.

4) ЛМ по п.1 в применении к документальным генеалогиям, и тем, для чего известны расчеты другими достоверными методами (например, по снипам). Правда, по снипам надо принимать во внимание, что там нет «бутылочных горлышек популяции», поэтому результаты расчетов по снипам будут или равны результатам расчетов по ЛМ, или давать завышенные результаты. Если есть и то, и другое, то это нормально.

5) ЛМ по 67– и 111-маркерным гаплотипам, и ККК (квадратичный по индивидуальным константам) по ним же.

6) ЛМ по 22-маркерным гаплотипам, и ККК по ним же.

7) «Медленные» 22-маркерные гаплотипы в сопоставлении с известными древними датировками.

8) Сопоставление расчетов по 111– и 67-маркерным гаплотипам с данными документальной генеалогии.

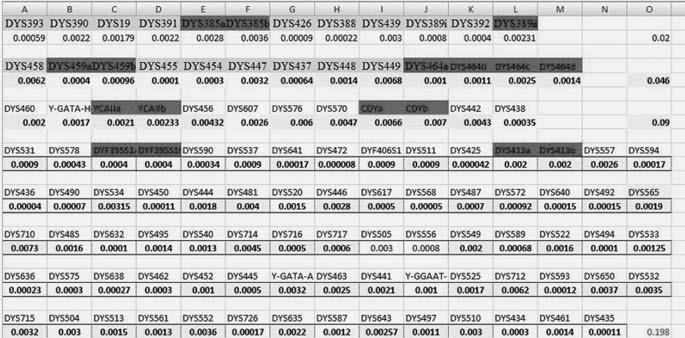
Рис. 9. Значения индивидуальных констант скоростей мутаций для 111 маркеров

Вопрос 66: Почему датировки по мутациям в гаплотипах и по снипам часто не совпадают?

Строго говоря, это разные датировки. Расчеты по мутациям в гаплотипах наших современников дают временное расстояние до общего предка выборки. Если выборка малая, нерепрезентативная, то она может дать заниженное или завышенное расстояние до общего предка. С увеличением размера выборки, или числа выборок по изучаемой территории (вплоть до всего континента или всей планеты) датировка постепенно стабилизируется, приходя к значению, которое можно принять за наиболее особно-ванное. По аналогии, если бросать монету всего немного раз, то усредненное значение «вероятности» выпадения орла или решки может быть завышенным или заниженным по сравнению с известной вероятностью 0.5, но при увеличении числа бросков это усредненное значение стабилизируется, приближаясь к 0.5.

Важно, что время жизни общего предка выборки современников из определенной и выбранной гаплогруппы вовсе не обязательно покажет датировку образования данной гаплогруппы. Популяция данной гаплогруппы могла пройти «бутылочное горлышко», при котором могли выжить только некоторые, и потомство могло выжить и дожить до наших дней только от одного человека, пережившего бутылочное горлышко. Тогда, разумеется, датировка общего предка будет более недавней, чем датировка образования рассматриваемой гаплогруппы.

В отличие от этого, датировка по снипам не ограничена вымираниями древних популяций, если остался хотя бы один мужчина, прямое потомство от которого дожило до наших дней. Тогда цепочка снипов проходит в его Y-хромосоме до общего предка с шимпанзе и древнее. В этом причина, почему «датировка общего предка выборки» или «датировка общего предка региона», даже обширного, часто не совпадают друг с другом.

Пример – субклад V13 гаплогруппы E1b. Датировка образования субклада по снипам (компания YFull) – примерно 7600 лет назад, с учетом погрешности, приведенной YFull – 7600±1300 лет назад. С этим согласуется археологическая датировка ископаемого субклада E1b-V13, обнаруженный на севере Испании – примерно 7000 лет назад. Для вычисления датировки общего предка выборки современных гаплотипов собрали 193 гаплотипа в 67-маркерном формате по всей Европе, и их дерево гаплотипов оказалось почти идеально симметричным:

Рис. 10. Дерево 193 гаплотипов в 67-маркерном формате субклада E1b-V13

Все 193 гаплотипа содержат 2857 мутаций, что дает 2857/193/0.12 = 123 ? 141 условных поколений до общего предка, то есть общий предок всей выборки жил 3525±360 лет назад[64]’ [65]. Мы столь подробно на этом останавливаемся, чтобы показать разрыв во времени между датировкой ископаемого гаплотипа группы E1b-V13, и датировкой общего предка современных носителей той же группы. Разрыв – почти четыре тысячи лет. На самом деле, разрыв, скорее всего, начался примерно 4500 лет назад, в ходе заселения континентальной Европы эрбинами, носителями гаплогруппы R1b, и продолжался тысячу лет. Это было время выживания ДНК-генеалогической линии E1b-V13, пока выживание не состоялось окончательно, то есть критический размер популяции был преодолен.

Теперь проверим, как ископаемый гаплотип соотносится с современными гаплотипами субкладаVl3. Ископаемый имеет вид

13 24 13 10 16 19 11 13 11 31 16 14 20 10 22

(ископаемый E1b-V13, Испания)

Предковый гаплотип, к которому сходится дерево, показанное выше, в 67-маркерном формате имеет вид

13 24 13 10 16 18 11 12 12 13 11 30–15 9 9 11 11 26 14 20 32 14 16

17 17 – 9 11 19 21 17 12 17 20 31 34 11 10–10 8 15 15 8 11 10 8 12 10

0 23 24 18 11 12 12 17 7 12 22 18 12 13 12 14 11 11 11 11

(предковый гаплотип E1b-V13, 3525 лет назад)

В маркерах, показанных для ископаемого гаплотипа, он редуцируется до следующего:

13 24 13 10 16 18 12 13 11 30 15 14 20 10 22

(предковый E1b-V13, 3525 лет назад)

Четыре мутации между гаплотипами (отмечены) разводят их на 2625 лет, и помещают их общего предка на (2625+3525+7000V2 = 6575±700 лет назад, что и соответствует датировке ископаемого гаплотипа в пределах погрешности расчетов. Таким образом, выжил, пройдя бутылочное горлышко популяции, прямой потомок «испанского» гаплотипа, и он принял эстафету рода, образовавшего сейчас дерево гаплотипов, показанное выше.

Напротив, для множества субкладов датировка для их образования по снипам и мутациям в гаплотипах, практически совпадают. Приведем всего несколько примеров – для субкладов I2a-S17250, l2a-Y4460 и I2a-Z17855, основных для носителей гаплогруппы I2a Восточной Европы, и снипы, и мутации в гаплотипах дали датировку 2300 лет назад. Для субклада R1a-Z280, который имеют половина этнических русских (наряду с субкладом R1a-M458), датировка по снипам и мутациям в гаплотипах дала 4900 лет назад, для субклада R1b-L23, основного субклада древнеямной культуры на территории современной России, потом переместившегося на Кавказ и в Месопотамию, датировка по снипам и мутациям в гаплотипах дала 6400±900 и 6000±600 лет, соответственно, и так далее.

Вопрос 67: В примере выше вы приводили значения констант скоростей мутаций и для отдельных маркеров, как DYS393 и DYS390, так и для всего гаплотипа, от 6– до 111-маркерного, и даже до 409-маркерного. Как же все-таки нужно считать, по отдельным маркерам или по целым гаплотипам?

Это – хороший вопрос, он часто служит предметом путаницы. Считать можно и по отдельным маркерам, и по целым гаплотипам, и это определяется целесообразностью в каждом конкретном случае, удобством, экономией времени.

Приведем пример – серию из 27 гаплотипов в 12-маркерном формате. Это – реальная серия гаплотипов из одного из проектов (киргизского) FTDNA.

13 24 16 10 11 14 12 12 10 13 11 18

13 24 16 11 11 14 12 12 10 13 11 18

13 24 16 11 11 14 12 12 10 14 11 17

13 24 16 11 11 14 12 12 10 14 11 18

13 25 16 10 11 14 12 12 10 14 11 18

13 25 16 10 11 14 12 12 10 14 11 18

13 25 16 10 11 14 12 12 10 14 11 19

13 25 16 10 11 14 12 12 10 14 11 19

13 25 16 11 11 14 12 12 10 13 11 18

13 25 16 11 11 14 12 12 10 13 11 18

13 25 16 11 11 14 12 12 10 13 11 18

13 25 16 11 11 14 12 12 10 13 11 18

13 25 16 11 11 14 12 12 10 14 11 17

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 18

13 25 16 11 11 14 12 12 10 14 11 19

13 25 16 11 11 14 12 12 10 14 11 19

13 25 16 11 11 14 12 12 10 15 11 17

13 25 17 11 11 14 12 12 10 14 11 18

13 26 16 11 11 11 12 12 10 14 11 17

Девять из них идентичны друг другу, это – базовые, или предковые гаплотипы. Они не успели мутировать за время, прошедшее от их общего предка. На все 27 гаплотипов приходится 27 мутаций (отмечены жирным шрифтом). Иначе говоря, за время, прошедшее от их общего предка, девять 12-маркерных гаплотипов полностью сохранились, 18 гаплотипов приобрели мутации. Популяционный генетик рассчитал бы «коэффициент разнообразия» гаплотипов, который никому и никогда не нужен, и на этом бы свою работу закончил соответствующей публикацией, а рецензент в журнале, тоже, естественно, попгенетик, статью бы без вопросов пропустил в печать. То, что это фактически мусор, ему бы и в голову не пришло, там «наука» такая. На самом деле эта серия гаплотипов позволяет расчитать, когда жил общий предок этих гаплотипов, и далее, прослеживая подобные гаплотипы по территориям, и каждый раз рассчитывая времена жизни общих предков, можно понять, в какую сторону направлялись древние миграции, и сопоставляя полученные данные с археологическими и лингвистическими показателями, можно получать более содержательные картины прошлого.

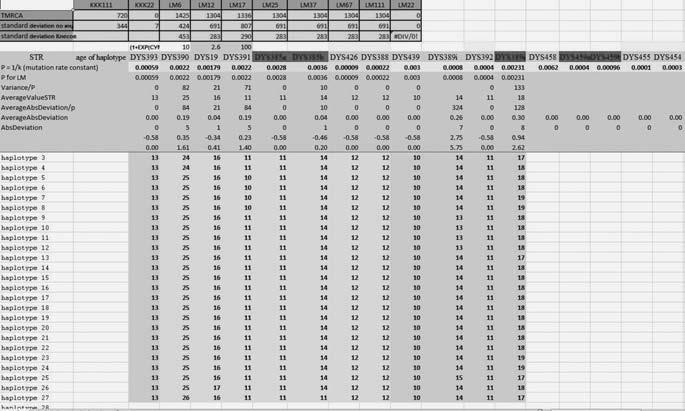
Рис. 11. Расчет времени до общего предка для 27 гаплотипов в 12-маркерном формате из Киргизского проекта FTDNA. Поскольку гаплотипы 12-маркерные, то же расстояние до общего предка (TMRCA), 1304±283 лет, повторено в колонке для 225-, 37-, 67– и 111-маркерных гаплотипов. Колонка для 6-маркерных гаплотипов показывает 1425±453 лет до общего предка, что является тем же самым в пределах погрешности расчетов. Остальными колонками следует пренебречь.

Так вот, рассчитать время жизни общего предка можно разными способами. Можно – используя все 12 индивидуальных констант (k) скоростей мутаций, и считать по каждому маркеру, раздельно. Их величины приведены выше, в ответах на вопрос 65. Тогда результатом расчета будет набор из 12 «времен жизни до общего предка», который следует усреднить Это – очень непродуктивный метод расчета, и так вручную никто не считает (тем более всего для 27 гаплотипов, с крайне бедной статистикой). Но это – основа для машинных (компьютерных) расчетов, особенно для сотен и тысяч гаплотипов, и итоговое усреднение проводится по всему полю данных. Именно так работает калькулятор Килина-Клёсова[66], в который заложены значения констант скоростей для 111 маркеров, и расчет проводится по массиву данных до 10 тысяч гаплотипов практически в любом формате. Время расчета даже для 10 тысяч 111-маркерных гаплотипов занимает всего несколько секунд. В данном случае у шести маркеров из 12 мутаций нет, так что для них формальное «время до общего предка» равно нулю, но оно усредняется с результатами по шести оставшимся маркерам, и суммарно оно оказывается равно 1304±283 лет до общего предка (без округлений). Скриншот калькулятора с экрана компьютера приведен на рис 11.

Мы видим и сами гаплотипы, которые вводятся в соответствующие ячейки в формате Excel – или вручную, или копируются целиком из соответствующего файла, и число мутаций по каждому маркеру (третья строка снизу на сером фоне), сумма которых равна в данном случае 27. В формате Excel сумму их не обязательно подсчитывать вручную, можно просто все высветить курсором и прочитать сумму на экране. Программа также показывает базовые (предковые) значения аллелей (шестая строка снизу на сером фоне), и много другой важной информации. Датировка времени жизни общего предка читается в колонке LM12, что означает «линейный метод (расчета) по 12-маркерным гаплотипам». В колонках для 25-, 37-, 67– и 111-маркерных гаплотипов появляется то же самое число лет, что и для 12-маркерных гаплотипов, и странно было бы ожидать другого. В других колонках числа не являются правильными, потому что для них просчитывается только часть маркеров (колонки для 17-маркерных и 22-маркерных гаплотипов, и обозначенные ККК, то есть квадратичный расчет для 111– и 22-маркерных гаплотипов). Для проверки работы калькулятора можно разделить число мутаций на число гаплотипов и на константу скорости мутации для 12-маркерных гаплотипов, 27/27/0.02 = 50 условных поколений без введения поправки на возвратные мутации, которая равна 1.0433. Эта поправка рассчитывается, как показано в ответе на вопрос 61. В данном случае средняя величина числа мутаций на маркер равна 27/27/12 = 0.0833, и формула для расчета поправки приобретает вид

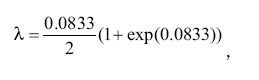
где величина поправочного коэффициента (1+e^0.0833)/2 равна 1.0433, и вместо 50 условных поколений получаем 52.165, что соответствует 1304 годам до общего предка, то есть в точности то, что выдал калькулятор. Погрешность при 27 мутациях рассчитывается путем обратной величины квадратного корня из 27, что есть 0.19245, возведением полученной величины в квадрат и прибавлением 0.01 (10 %-й погрешности для константы скорости мутации), получая 0.0470, и после извлечения квадратного корня получаем общую погрешность в ±21.69 %. Окончательно записываем, что датировка общего предка рассмотренной серии из 27 гаплотипов равна 1304±283, в точности то, что рассчитал калькулятор, только в данном случае он рассчитал за долю секунды.

Надо заметить, что калькулятор выдает такую точность, которая не только бессмысленна, но и неправильна, потому что расстояние до общего предка с точностью до одного года не бывает, и погрешность с точностью до одного года не определяется. Поэтому полученную величину следует округлить, например, так: 1300±280 лет до общего предка.

Еще один способ расчета называется логарифмическим[67], в котором мутации даже не считаются. Поскольку в серии из 27 гаплотипов 9 базовых, то получаем [ln(27/9)]/0.02 = 55 ? 58 условных поколений, то есть 1450±500 лет до общего предка. Как видно, это в пределах погрешности расчетов совпадает с величиной, полученной и линейным способом, и с помощью калькулятора Килина-Клёсова. Для концептуальных выводов это вполне приемлемо. Концептуальными здесь называются выводы (или результаты), которые ставят задачей расчеты с точностью, которая позволяет сделать принципиальные выводы, например, исторического характера. Как известно, историки и археологи часто оперируют концептуальными положениями, например, что скифы играли роль на исторической арене примерно с 7-го века до начала нашей эры, сарматы – с начала нашей эры до примерно 4-го века нашей эры, кельты – примерно с 4-го века до н. э., хотя есть варианты. Иначе говоря, в этих случаях датируются не конкретные события, а концептуальные. ДНК-генеалогия часто очень полезна в таких случаях. Например, что общий предок этнических русских гаплогруппы R1a и общий предок индийцев высших каст гаплогруппы R1a жил практически в одно и то же время. В пределах погрешности измерений, это был – концептуально – один и тот же общий предок. Никто не ожидает там датировку с точностью до года или около того. Речь – о концепции, а не о точной формальной датировке.

Вопрос 68: Как измеряют константы скоростей мутаций?

Часто приходится слышать, что если скорости мутаций такие малые, что одна мутация происходит порой раз в несколько тысяч лет, то как же их измеряют? Скептики тут же заключают, что эти величины недостоверны, поскольку эксперименты длиной в тысячи лет невозможны. Это только показывает ментальную удаленность скептиков от науки. Аналогия – времена полураспада многих радиоактивных элементов составляют тысячелетия или намного большие времена – например, период полураспада радия-226 составляет 1620 лет, а урана-238 – 4.5 миллиарда лет. Никто из исследователей не сидит и не ждет, пока половина вещества распадется.

Один из подходов при измерении величин констант скоростей мутаций – сопоставление гаплотипов в парах отец-сын. Если изучается группа, например, в 2000 пар отец-сын, то среднее количество мутаций между их гаплотипами определяется по формуле x/2000/k = 1, где х – количество мутаций, k – константа скорости мутаций.

Чтобы понять, сколько мутаций можно ожидать в таких опытах, приведем список диапазонов констант скоростей мутаций[68](в числе мутаций за условное поколение, то есть за 25 лет), из полного списка выше.

Ниже приведены самые «медленные» 22 маркера в 67-маркерной панели:

DYS472 0.000008

DYS436 0.000040

DYS425 0.000042

DYS568 0.000050

DYS490 0.000070

DYS426 0.000090

DYS455 0.000100

DYS450 0.000110

DYS492 0.000150

DYS640 0.000150

DYS641 0.000170

DYS594 0.000170

DYS388 0.000220

DYS454 0.000300

DYS590 0.000340

DYS438 0.000350

DYS392 0.000400

DYF395Sib 0.000400

DYF395Sia 0.000400

DYS459a 0.000400

DYS578 0.000430

DYS617 0.000500

Все они, кроме DYS459a, образуют «медленную» 22-маркерную панель для расчетов особенно удаленных по времени общих предков серий гаплотипов. Маркер DYS459a в 22-маркерную панель не включен, поскольку для него характерен так называемый палиндромный, или «мультимаркерный» эффект, при котором при мутациях маркеры меняются синхронно, парами. Правда, этот эффект присущен также маркерам DYF395S, но так уж сложилось, что они вошли в эту панель. Вместо DYS459a в 22-маркерную панель введен DYS531.

Самые медленные маркеры панели от маркеров от 68 до 111 следующие:

DYS632 0.000100

DYS494 0.000100

DYS435 0.000110

DYS593 0.000120

DYS726 0.000170

DYS636 0.000230

DYS638 0.000270

DYS575 0.000300

DYS434 0.000300

DYS462 0.000300

DYS445 0.000500

DYS716 0.000500

Самые «быстрые» маркеры в 111-маркерной панели следующие:

DYS710 0.007300

CDYb 0.007000

DYS449 0.006800

CDYa 0.006600

DYS712 0.006200

DYS458 0.006200

DYS576 0.006000

DYS570 0.004700

DYS714 0.004500

DYS456 0.004320

DYS442 0.004300

DYS481 0.004000

Мы видим, что самые «медленные» маркеры мутируют со средней скоростью от 0.000008 мутаций в поколение (то есть в среднем раз в 125 тысяч поколений, или более чем в 3 миллиона лет) до 0.00050 мутаций в поколение (в среднем раз в 2000 поколений, или примерно раз в 50 тысяч лет). Можно эти числа объяснить по-другому – наиболее «медленные» мутации происходят в среднем раз на 125 тысяч рождений мальчиков (DYS472), или раз на 125 тысяч пар отец-сын, до одного раза на 2000 рождений мальчиков, или один раз на 2000 пар отец-сын. Отсюда уже ясно, что большинство из приведенные выше «медленных» маркеров практически бесполезны на парах отец-сын, потому что подавляющее большинство из них вообще не дадут мутаций даже на 2000 парах, в лучшем случае некоторые дадут одну мутацию, из которых константу скорости не вычислить, погрешность таких расчетов составит плюс-минус 100 % даже при доверительном интервале в 68 % (одна сигма). Поразительно, что популяционные генетики используют такие «скорости мутаций», расчитанные из одной мутации, или даже без единой мутации в парах отец-сын (приведенные, например, в работах[69], [70]), даже не задумываясь, что смысла в этом нет практически никакого. Естественно, получают при этом невоспроизводимые «времена жизни общих предков», и объявляют, что по мутациям в гаплотипах считать нельзя (D. Pontikos[71]; Busby et al[72]).

Самые «быстрые» маркеры мутируют в среднем от частот (1/0.0073) один раз в 137 условных поколений, то есть примерно раз в 3400 лет, или один раз на 137 рождений мальчиков, до примерно (1/0.004) один раз в 250 условных поколений. Давайте посмотрим, как это выглядит на практическом примере. Воспользуемся тем же набором из 3466 гаплотипов гаплогруппы R1b-L21. В маркере DYS472, самом «медленном», аллели образуют следующий набор:

7 – 1 (то есть аллель 7 встречается в 3466 маркерах DYS472 всего один раз)

8 – 3461 раз

9 – 4 раза

Таким образом, мы наблюдаем всего пять мутаций на 3466 маркеров DYS472 за 152 условных поколений (расчеты см. выше), прошедших со времени жизни общего предка этих гаплотипов. Это дает константу скорости мутации, равную примерно 5/3466/152 = 0.95 ? 10^-5 мутаций на условное поколение. Если давать более строгую формулировку, то при пяти мутациях надо написать (0.95±0.43) ? 10^-5 мутаций на условное поколение, или, что более правильно, (1.0±0.4) ? 10^-5 мутаций на условное поколение. Погрешности здесь рассчитываются по обычным правилам статистики, как квадрат обратной величины квадратного корня из числа мутаций. Здесь мы пренебрегли поправкой на возвратные мутации, потому что она в данном случае практически ничего не меняет, поправка составит менее одной сотой доли процента.

Но этот расчет проведен только на одной серии гаплотипов. В серии из 976 гаплотипов гаплогруппы R1a в маркере DYS472 прошла всего одна мутация, что при 154 условных поколениях до общего предка дает константу скорости мутации 1/976/154 = 0.67 ? 10^-5 на условное поколение. В целом, при подобном рассмотрении серий гаплотипов из 24 разных субкладов средняя величина для константы скорости мутации для DYS472 оказалась равной 0.8 ? 10^-5 мутаций на условное поколение.

Заметим, что это – самая «медленная скорость мутации из всех 111 маркеров. Для остальных задача решается еще проще, там мутаций больше.

Приведем еще несколько примеров «медленных» маркеров, расчеты по которым самые сложные. По парам отец-сын они вообще не определяются. Например, маркер DYS455. В серии из 3466 аллелей этого маркера наблюдаем следующее распределение:

9 – 6 (то есть аллель 9 встречается в 3466 маркерах DYS455 всего 6 раз)

10 – 28

11 – 3409

12 – 23

Считая, что все мутации одношаговые, получаем 63 мутации на 3466 аллелей DYS455 за те же 152 условных поколения, прошедших со времени жизни общего предка этих гаплотипов. Это дает константу скорости мутации, равную 63/3466/152 = 0.00012±0.00002 мутаций на маркер DYS455 за условное поколение. Поправка на возвратные мутации здесь составляет менее одного процента, поэтому вводить ее бессмысленно. В таблице выше дана константа скорости 0.00010, усредненная из многих расчетов по разным гаплогруппам.

Маркер DYS594:

7 – 1

8 – 2

9 – 4

10 – 3401

11 – 58

В сумме это дает 69 мутации на 3466 аллелей DYS594 за 152 условных поколения до общего предка. Это дает константу скорости мутации, равную 69/3466/152 = 0.00013±0.00002 мутаций на маркер DYS594 за условное поколение. Поправка здесь тоже составляет менее одного процента, поэтому вводить ее не будем. В таблице выше дана константа скорости 0.00017, усредненная из многих расчетов по разным гаплогруппам.

Маркер DYS490:

11 – 4

12 – 3437

13 – 18

14 – 7

В сумме это дает 36 одношаговых мутаций на 3466 аллелей DYS490 за 152 условных поколения до общего предка. Это дает константу скорости мутации, равную 36/3466/152 = 0.00007±0.00001 мутаций на маркер DYS594 за условное поколение. Поправка здесь тоже составляет менее одного процента, поэтому вводить ее не будем. В таблице выше дана константа скорости 0.00007, усредненная из многих расчетов по разным гаплогруппам, то есть точно такая же, как рассчитанная выше.

Маркер DYS492:

11 – 44

12 – 3398

13 – 22

14 – 2

В сумме это дает 70 одношаговых мутаций на 3466 аллелей DYS492 за 152 условных поколения до общего предка. Это дает константу скорости мутации, равную 70/3466/152 = 0.00013±0.00002 мутаций на маркер DYS492 за условное поколение. Поправка здесь тоже составляет менее одного процента. В таблице выше дана константа скорости 0.00015, усредненная из многих расчетов по разным гаплогруппам, то есть в пределах погрешности такая же, как рассчитанная выше.

А теперь приведем несколько примеров того, к чему приводят «быстрые» константы скоростей мутаций. Рассмотрим самую «быструю» – DYS 710, которая входит в 111-маркерную панель. Этот маркер не изучался в экспериментах на примерно 1700 парах отец-сын[73], как и многие другие маркеры. Точнее, там вообще не изучались 24 маркера, в 17 маркеров мутаций не было, в 15 маркерах прошла всего одна мутация, то есть 56 маркеров из 111 оказались непригодными для количественного определения скоростей мутаций. А поскольку еще в 11 маркерах прошли всего две мутации, то почти две трети всех маркеров оказались непригодными для определения констант скоростей мутаций.

Даже при одной сигма (доверительный интервал плюс-минус 68 %) погрешность в определении скоростей мутаций (точнее, констант скоростей мутаций) составляет ±100 % при одной мутации, и ±71 % при двух мутациях. А попгенетики их используют, в том числе и те маркеры, в которых мутаций вообще не было, при этом умудряясь рассчитать «скорости мутаций» для тех маркеров! В результате, разумеется, опять мусор в академических публикациях. Пример такой работы – исследование 2013 года[74], в авторах которого Chris Tyler-Smith, один из ведущих популяционных генетиков мира, и журнал один из ведущих. Я немедленно написал критическую статью в тот же журнал, и началась типичная для попгенетиков ситуация. Полгода ответа от журнала вообще не было. Я написал напоминание. После этого пришла одна рецензия, совершенно уклончивая, суть которой состояла в том, что несправедливо критиковать исследование, в котором используются мутации, определенные по парам отец-сын, поскольку многие их применяют. Поэтому моя статья быть принята не может. Я написал ответ, выразив возмущение сроками рецензии – более полугода, а также тем, что рецензент всего один, и само замечание неквалифицированное.

Через месяц пришла еще одна рецензия, в которой опять предлагалось снять критику за использование «скоростей мутаций» по парам отец-сын, снять таблицу, в которой показано, что значительная часть маркеров, используемых в работе Tyler-Smith, основывается всего на нескольких мутациях в парах отец сын. Так, по разным цитируемым авторами данным, в маркере DYS643 мутаций вообще не было, в DYS448, и DYS549 прошло всего по одной мутации (в 1213 и 555 парах отец-сын, соответственно), маркерах DYS533 и DYS 438 по две мутации (в 555 и 4565 парах отец-сын, соответственно), и это уже шесть маркеров из 21, используемых в работе, более четверти. Помимо того, в работе использовались печально известные «популяционные скорости Животовского», которые вообще завышали датировки в три раза. Я ответил, что ничего снимать не буду. После этого получил письмо уже от главного редактора с приложением еще одной рецензии. Суть ее была в том, что несправедливо критиковать именно эту статью, и особенно несправедливо по отношению к Tyler-Smith, поскольку то, о чем я пишу, характерно по отношению почти ко всем статьям популяционных генетиков, и почему начинать именно с Tyler-Smith? Поэтому мне предлагалось вообще снять всю критику данной статьи, и написать общую статью по скоростям мутаций в гаплотипах. Я отказался, написав, что сначала пусть они публикуют эту критическую статью, а потом обсудим более общую статью. После этого в течение года редактор мне регулярно напоминал, что они ждут общую статью, но о критической статье не упоминал. Но мне статьи не очень нужны, у меня их более пятисот, и более двадцати книг, поэтому я и не отвечал. Такое отношение к авторам мне не подходит. И после этого попгенетики еще мне высказывают претензии, что я не публикуюсь в журналах по популяционной генетике. Нет уж, меня ангажированные издания не устраивают.

Возвращаемся к «быстрым» скоростям мутаций. В маркере DYS710 в рассмотренном выше списке из 3466 гаплотипов (и, соответственно, аллелях данного маркера) наблюдается следующая картина распределений:

29 – 1 (то есть аллель 29 встречается в 3466 маркерах DYS710 всего один раз)

30 – 21 раз

31 – 49 раз

32 – 93

33 – 427

34 – 808

35 – 1058

36 – 759

37 – 182

38 – 50

39 – 17

40 – 1 раз

Видно, что картина мутаций значительно более «размазанная» по сравнению с медленными константами скоростей. Считая, что все мутации одношаговые, получаем 3594 мутации на 3466 аллелей DYS710 за те же 152 условных поколения, прошедших со времени жизни общего предка этих гаплотипов. Мы видим, как высокие скорости мутаций «размазывают» распределение мутированных аллелей в широком диапазоне. Если при минимальной скорости мутаций в DYS472 сохранились неизменными 3461 предковые аллели в гаплотипах 3466 потомков (константа скорости мутации 0.000008 на условное поколение), и в DYS617 сохранились неизменными 2921 предковые аллели в гаплотипах 3466 потомков (константа скорости мутации на в 63 раза выше, 0.0005 на условное поколение), то в случае самого «быстрого» маркера сохранились всего 1058 предковые (базовые) аллели, и число мутаций равно 3594 вместо 5 в DYS472, то есть в 700 с лишним раз больше. Константа скорости мутации была бы равна 3594/3466/152 (без учета поправки на возвратные мутации), то есть была бы равна примерно 0.0068 мутаций на условное поколение. Но из-за высокой скорости мутаций настолько много, что отношение числа мутированных аллелей к общему числу аллелей превышает единицу (3594/3466 = 1.037), и поправки на возвратные мутации «захлебываются», дают заниженные показатели, и в целом перестают работать. Формальный расчет по формуле, приведенной выше, показывает, что число возвратных мутаций здесь практически равно числу «прямых» мутаций, и полученную величину 0.0055 нужно удвоить. В действительности усредненная контанта скорости мутации этого маркера по разным гаплогруппам равна 0.0073 на условное поколение (25 лет), и она приведена в таблице выше.

Еще пример относительно «быстрого маркера» – это DYS534. В том же списке из 3466 гаплотипов (и, соответственно, аллелях данного маркера) наблюдается следующая картина распределений:

12 – 3 раза

13 – 48

14 – 524

15 – 1574

16 – 1043

17 – 229

18 – 43

19 – 2

Считая, как обычно, что все мутации одношаговые, получаем 2267 мутаций на 3466 аллелей DYS534 за те же 152 условных поколений, прошедших со времени жизни общего предка этих гаплотипов. Мы видим, что по сравнению с самым «быстрым» маркером DYS710 (в котором сохранились всего 1058 предковых (базовых) аллелей, и число мутаций равно было 3594, в случае DYS534 сохранилось 1574 предковых аллелей, и общее число мутаций равно 2267. Давайте посмотрим, что получится в этом случае. Константа скорости мутации, получаемая из экспериментальных данных, равна 2267/3466/152 (без учета поправки на возвратные мутации), то есть равна примерно 0.00430 мутаций на условное поколение. Моделирование дает среднюю константу скорости 0.00315 мутаций на условное поколение по разным гаплогруппам.

Таким образом можно проводить расчет констант скоростей мутаций, используя большие серии гаплотипов. Но работа на этом не заканчивается, потому что серии гаплотипов могут быть искаженными, включать примеси из других серий, с другим общим предком, включать другие субклады, с другим распределением аллелей по частотам, и так далее. Поэтому получаемые значения констант скоростей мутаций необходимо калибровать по известным документальным генеалогиям, опять желательно по нескольким. Как это делается, мы увидим в следующем разделе.

Вопрос 69: Насколько константы скоростей мутаций, определенные в разных регионах мира, надежны для проведений расчетов в ДНК-генеалогии? Что такое «калибровка» констант скоростей мутаций?

Приведу некоторую аналогию – а насколько надежны расчетные скорости (на самом деле – константы скоростей) радиоактивного распада соответствующих веществ? Влияют ли на них регионы планеты, где проводятся измерения? Любой образованный человек ответит – конечно, нет, не влияют. Скорость распада радиоактивных материалов определяется исключительно «внутренними» свойствами вещества, а не внешними воздействиями. Это – фундаментальные показатели. Вот так же должен отвечать каждый образованный человек на соответствующий вопрос о константах скоростей мутаций в гаплотипах. Это – фундаментальные показатели. Никакие регионы, питание, физические упражнения, национальность, гражданство или партийная принадлежность на них не влияют. Естественно, речь здесь идет о нормальных условиях, а не, скажем, в условиях солнечного ядра, или при смертельных уровнях радиации.

Итак, мутации в гаплотипах потомков расходятся от предкового гаплотипа как круги по воде, число мутаций легко рассчитывается, и они подчиняются довольно простым количественным закономерностям. Для кругов на воде, расходящихся от места, куда был брошен камень, легко рассчитать, когда был брошен камень, если знать скорость распространения волны и место нахождения круговой волны в данный момент времени. Чем больше прошло времени – тем дальше круги ушли, тем больше они разошлись. Так и в гаплотипах – чем больше время, прошедшее от общего предка, тем больше мутаций накопилось в гаплотипах его потомков. Число этих мутаций связано с временем, прошедшим от общего предка, с числом гаплотипов в серии, и с константой скорости мутации в гаплотипах, и выражается простой формулой: n/N = kt, где n – число мутаций в серии из N гаплотипов, k – константа скорости мутации (в числе мутаций на гаплотип за условное поколение, равное 25 лет), t – число условных поколений, с табличной поправкой на возвратные мутации[75]. На сотнях и тысячах примеров показано, что эта формула работает при любом числе гаплотипов и мутаций в них, и при любом времени, прошедшем от общего предка рассматриваемых гаплотипов. Однако при очень больших временах, более 10–20 тысяч лет, и особенно более 100 тысяч лет, нужно использовать гаплотипы с «медленными» маркерами, то есть с малыми константами скоростей мутаций, и тем самым снижать число мутаций и число возвратных мутаций. По аналогии, вряд ли целесообразно изучать скорости радиоактивного распада элементов со временами полураспада в тысячелетия, используя секундомер. Или пытаться изучать круги на воде за километры от места, куда был брошен камень, для этого нужно значительно более мощное воздействие. Как всегда, нужен конкретный анализ в конкретной ситуации, единых подходов на все случае жизни не бывает. Варианты конкретного анализа в конкретных ситуациях и рассматривает ДНК-генеалогия. Некоторые ситуации и расчеты мы рассмотрим ниже.

Теперь вопрос – насколько надежны величины констант скоростей мутации в соответствующих маркерах Y-хромосомы? Они надежны настолько, насколько надежно их определяют, калибруют, проверяют исследователи. Когда это делают популяционные генетики – совершенно ненадежны, они это показали последними двадцатью годами их так называемых «исследований». Они до сих пор так и не знают, какие значения эти константы имеют. Они до сих пор, в академических статьях 2015 года, продолжают использовать «скорости Животовского»[76]. Причем «на полном серьезе» обсуждают, что на временах до 5 тысяч лет эти «скорости» сильно завышают датировки, и вот на временах 40–60 тысяч лет подходят в самый раз. Они так и не поняли, что 23-маркерные гаплотипы на временах 40–60 тысяч лет вообще не применимы, там больше половины столь «быстрых констант скоростей», что они вообще не работают, потому что мечутся как белка в колесе. Это все равно, что секундомером измерять астрономические явления продолжительностью в тысячи и миллионы лет. И попгенетики этого так еще и не поняли!

Иногда принцип датировки «разбега» мутаций в гаплотипах с течением времени называют «принципом молекулярных часов». Смысл в этом есть, но примитивный. Дело не в том, что часы, а в том, чтобы правильно ходили. Любая реакция в химических или биологических системах, описываемая константой скорости первого порядка, есть «обычные молекулярные часы», поскольку связана с хронологией процесса на молекулярном уровне. Динамика любого такого процесса связана с временем согласно формуле с = с₀е^-kt, где c₀ – исходное состояние системы (например, начальное количество или концентрация изучаемого вещества; количество гаплотипов Y-хромосомы в изучаемой выборке, и т. д.), с – состояние системы в определенный момент времени t (где t – время прошедшее с начала реакции, t-t_o), или количество базовых, то есть исходных гаплотипов в изучаемой выборке в настоящее время, спустя время t, прошедшее со времени жизни общего предка изучаемой серии гаплотипов), k – константа скорости реакции (мутаций, в данном случае). Эту же формулу можно переписать в виде ln(c_o/c) = kt, и она становится выражением логарифмического метода анализа выборок гаплотипов в ДНК-генеалогии. Берем, скажем, сто или тысячу гаплотипов, или любое другое их число, делим на число базовых (то есть одинаковых, идентичных друг другу гаплотипов, суть предковых гаплотипов, которые не успели мутировать за время t, прошедшее со времени жизни общего предка), берем натуральный логарифм (ln), и получаем произведение kt, то есть константу скорости мутации, помноженную на число лет, прошедшее со времени жизни общего предка, или на число условных поколений, опять же прошедших после общего предка – в зависимости от того, выражали константу скорости в годах, или в поколениях.

Логарифмический метод будет обсуждаться в следующем разделе, а пока обратим внимание, что результаты расчетов в ДНК-генеалогии обычно получаются в виде произведения kt. Это относится и к логарифмическому методу (см. выше), и к так называемому линейному методу, в котором считают число мутаций в серии гаплотипов, происходящих от одного общего предка, и делят их на число гаплотипов и на константу скорости мутаций в гаплотипе.

Отсюда уже видно, что неважно, сколько лет положить на условное поколение – 20, 25, 30, 35 или любое другое число лет, поскольку константа скорости мутации тут же подстроится, они завязаны друг на друга, произведение-то одно. В ДНК-генеалогии, как отмечалось выше, берется 25 лет на условное поколение, и, соответственно, константы скорости мутации приобретают определенные значения, получаемые по калибровке (см. ниже). Например -

для 12-маркерных гаплотипов константа равна 0.02 мутаций на гаплотип на условное поколение,

для 25-маркерных 0.046 мутаций на гаплотип на условное поколение,

для 37-маркерных – 0.09,

для 67-маркерных – 0.12,

для 111-маркерных – 0.198 мутаций на гаплотип на условное поколение.

Если это пересчитать в расчете не на гаплотип, а на маркер, то получим соответствующие константы скорости 0.00167, 0.00184, 0.00243, 0.00179, 0.00178 мутаций на маркер на условное поколение. Уже видно, что константы скорости разные для разных гаплотипов, и различаются, например, для 37-маркерных и 12-маркерных гаплотипов в 1.46 раз, то есть на 46 %. А если сравнить с 6-маркерными гаплотипами (константа скорости мутации на гаплотип равна 0.0074, на маркер 0.00123), то диапазон различий в константах в зависимости от длины маркера расходится на уже на 1.98, или на 98 %. Вывод – никак нельзя принимать константы скорости мутации на маркер за постоянные величины, одинаковые для всех гаплотипов, как делают в своих расчетах популяционные генетики. 98 % ошибки в расчетах только за это допущение – цена такого неумного (или неквалифицированного, или некомпетентного) предположения. Иначе говоря, иметь часы – дело нехитрое, но надо, чтобы они были отрегулированы. Это означает, что к ним должны прилагаться корректные константы скоростей мутаций, а корректные величины получаются корректной калибровкой.

Подходим к вопросу о калибровке констант скоростей мутаций.

Данные по калибровке были опубликованы в 2011 году в журнале Advances in Anthropology[77], и недавно изложены в популярном виде на Переформате (http://pereformat.ru/2014/11/dna-calibration/). Суть в том, что были взяты генеалогические данные для 13 семей, удовлетворяющие сформулированным жестким критериям. Эти 13 семей (или «Проектов») были отобраны из сотен других, которые были менее многочисленны или датировки которых были менее достоверны, или гаплотипы были короткими, то есть низкого разрешения.

В указанной статье[78] приведены многочисленные графики для гаплотипов разной протяженности, и каждый график иллюстрировал надежность калибровки, доверительные интервалы и прочее. Статья – редкая по глубине обоснований и достоверности полученных данных, результаты калибровок выверены на 3160 гаплотипах из 55 гаплогрупп и субкладов, из них 2489 гаплотипов были 67-маркерными.

Не будем приводить все калибровочные графики, дадим только калибровочную диаграмму для 37– и 67-маркерных гаплотипов. На рис. 12 на горизонтальной оси – число лет до общего предка каждой из документированных ДНК-генеалогических «семей», на вертикальной оси – среднее число мутаций на маркер (поскольку гаплотипы разные – 37– и 67-маркерные) в гаплотипах, принадлежащих этим семьям.

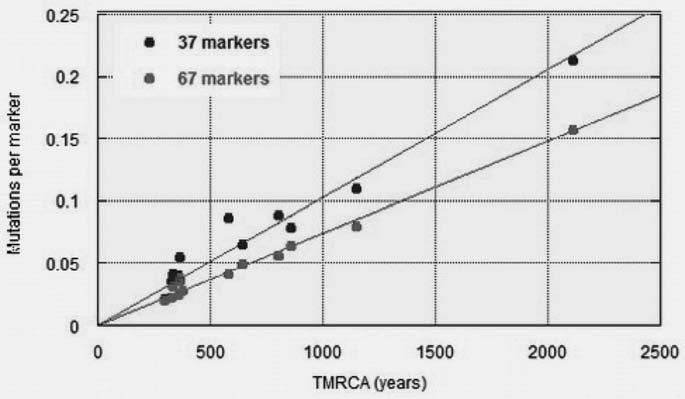
Рис. 12. Калибровочные взаимоотношения между временем, прошедшим от общих предков генеалогических серий гаплотипов в каждой группе («генеалогической семье»), и числом мутаций, накопившхся с того времени, в расчете на маркер в гаплотипах в 37– и 67-маркерном формате. Данные и принцип подхода опубликованы в журнале Advances in Anthropology (2011, Rozhanskii & Klyosov) и приведены в дополненном виде И.Л. Рожанским на Переформате (http://pereformat.ru/2014/11/dna-calibration/).

Видно, что есть четкая линейная зависимость между «возрастом» ДНК-линии и числом мутаций на маркер. Так и должно быть, поскольку мутации в гаплотипах (и маркерах) происходят случайным образом и описываются кинетикой первого порядка. Угол наклона корреляционной прямой для 37-маркерных гаплотипов выше, чем у 67-маркерных, поскольку мутации в 37 маркерах (где большая доля «быстрых» по мутациям маркеров) в совокупности происходят чаще, чем в 67-маркерных (где, напротив, маркеры с 38 до 67-го по порядку содержат высокую долю «медленных» маркеров). Отсюда и получились те константы скоростей мутаций, приведенные выше в данной статье: для 37-маркерных гаплотипов 0.00243 мутаций на маркер (0.09 мутаций на гаплотип) за условное поколение, для 67-маркерных гаплотипов 0.00179 мутаций на маркер (0.12 мутаций на гаплотип) за условное поколение. Для 67-маркерных гаплотипов точность калибровки больше, и соответствует погрешности в определении константы скорости мутаций ±2.5 %[79]. Рассмотрение тех нескольких тысяч гаплотипов, упомянутых выше, из 55 гаплогрупп и субкладов позволило заключить, что использованная калибровка и метод расчета дают точность в определении времени жизни предка с точностью ±10 % или меньше в интервале от 500 до 6000 лет назад.

Вопрос 70: Могло ли быть так, что мутации в ДНК в одном регионе планеты возникали с большей частотой, чем в другой (скажем, в местах, где радиоактивность была выше или по каким-то климатическим причинам и т. п.)?

Нет, не могло, если речь идет об обратимых мутациях в гаплотипах.

Часто слово «мутации» люди понимают ограниченно, как поломка чего-то в живых организмах под влиянием внешних воздействий, обычно радиации. Но в гаплотипах – это не поломка. Это процесс филигранной перестройки, перемещения блоков нуклеотидов в ДНК. Выше в этой книге был уже приведен пример строения маркера DYS393, в котором четверка нуклеотидов AGAT, то есть аденин-гуанин-аденин-тимин, повторяется определенное количество раз. Например, 13 раз, как у большинства носителей разных гаплогрупп:

и эти повторы обрамляются уже неупорядоченными последовательностями нуклеотидов в ДНК, как показано выше. И вот «мутация» приводит к тому, что вместо 13 раз эта четверка стала повторяться у потомков 12 или 14 раз, в результате однократной ошибки копирующей ДНК-полимеразной системы. Ну как радиация это сможет сделать? В любом случае, этого никто не показал, поэтому и вопроса как такового нет. Мы же не спрашиваем, могут ли на скорость мутации повлиять инопланетяне? Спросим, когда к такому вопросу появятся основания. Пока их нет.

Но выше шла речь в основном о мутациях в гаплотипах, с их филигранными перестройками, с вопроизводимыми константами скоростей. А вот в случае снипов картина может быть значительно более сложной и намного менее воспроизводимой. Там мутации не филигранны, там часто просто «поломки», простые превращения одного нуклеотида в другой, делеции (то есть просто выпадения нуклеотидов, иногда сразу нескольких) и прочие повреждения. Вот там внешняя среда может и влиять на мутации и частоту их появления, просто это пока мало изучено. Возможно, это поставит определенные и немалые ограничения для датировок по снип-мутациям. Иногда это видно даже простым глазом – например, выявляются десяток снип-мутаций там, где должны быть просто одна-две, чтобы было соответствие с уже выявленными закономерностями. Поэтому по снип-мутациям ошибки пока очень велики, возможно, такими и останутся.

Вопрос 71: Как производят расчет времен до общего предка серии гаплотипов?

По определению, чтобы рассчитать время до общего предка серии гаплотипов, необходимо, чтобы данная серия происходила от одного общего предка. Другими словами, чтобы современные носители этих гаплотипов все происходили от одного общего предка, в отношении которого производятся расчеты. Это, казалось бы, совершенно очевидное правило, игнорировалось популяционными генетиками на протяжении последних 20 лет, то есть практически всегда.

Давайте посмотрим, к чему это приводило и продолжает приводить попгенетиков.

Начиная с 1997 года время от времени выходят статьи израильских (в основном) популяционных генетиков, которые раз за разом утверждают, что они идентифицировали предковый гаплотип прародителя «ветхозаветных первосвященников», коэнов, который по их расчетам по мутациям в гаплотипах жил по разным расчетам между 3000 и 2600 лет назад. Он якобы имел следующий 6-маркерный гаплотип (маркеры DYS19, DYS388, DYS390, DYS391, DYS392, DYS393), который получил название «модального гаплотипа коэнов» (МГК):

14 16 23 10 11 12

В статье[80] рассматривали 306 гаплотипов евреев из Израиля, Канады и Англии, и нашли 112 вариантов гаплотипов. Из них отобрали те, которые близки к «модальному гаплотипу коэнов», исключили из рассмотрения DYS388, и в оставленных 5-маркерных гаплотипах нашли, что среднее отклонение их от усеченного МГК равно 0.226 мутаций на маркер. Поскольку авторы принимали, что средняя скорость мутаций в этих 5-маркерных гаплотипах равна 0.0021 на маркер на поколение (продолжительность поколения не была определена), то общий предок всех отобранных гаплотипов жил, по мнению авторов, 0.226/0.0021 = 108 поколений назад. У авторов при этом делении получилось 106 поколений назад, но это уже несущественно. Авторы написали, что если брать 25 лет на поколение, то общий предок жил 106х25 = 2650 лет назад, а если брать 30 лет на поколение, то он жил 3180 лет назад. Можно было бы и не упоминать, но со средней скоростью мутаций на маркер в данных гаплотипах авторы тоже ошиблись, она равна 0.00171, а не 0.0021 мутаций на маркер, и общий предок тогда жил якобы 132 поколения, или 3300 лет назад (при 25 годах на поколение) или 3960 лет назад (при 30 годах на поколение). Действительно, можно было бы не упоминать, потому что основная ошибка авторов не в делениях одного на другое, а в том, что ими постулировалось, что все рассматриваемые гаплотипы происходят от одного общего предка, хотя это оказалось, как мы покажем ниже, не так. Авторы по сути просто усреднили «отклонения величины аллелей от средней», а там были гаплотипы по меньшей мере от двух разных предков, один из которых, самый основной по количеству гаплотипов в выборке, жил всего тысячу лет назад. Никаким «ветхозаветным священником» он не был. Авторы на самом деле рассматривали разные ДНК-генеалогические линии, усредняя их, как берут хрестоматийную «среднюю температуру по больнице». Так работает популяционная генетика.

Следующая статья по гаплотипам евреев[81] могла бы прояснить ситуацию, но для попгенетиков не прояснила. В статье были опубликованы 194 гаплотипа в 6-маркерном формате, из которых 91 гаплотип были идентичны друг другу, и соответствовали «модальному гаплотипу коэнов» (см. выше). Авторам должно было быть ясно, что когда половина гаплотипов представляют собой предковый гаплотип, то предок явно не древний, и не мог жить больше 3 тыс лет назад, раз половина гаплотипов не успела мутировать. Но ясно бывает тогда, когда есть соответствующие знания, «ощущение ситуации». У авторов этого, очевидно, не было. А в другой половине (точнее, в 103 гаплотипах из 194) имелось 263 мутаций от «модального гаплотипа коэнов». Если бездумно разделить общее число мутаций на общее число гаплотипов и на константу скорости мутации 0.0074 на 6-маркерный гаплотип на поколение, 263/194/0.0074, то получим 183 ^224 условных поколений (стрелка показывает поправку на возвратные мутации), или 5600±660 лет до общего предка «гаплотипов коэнов». Это неразумно высокая величина, намного превышающяя времени жизни библейского Аарона по любым библейским интерпретациям, который по толкованию Библии жил примерно 3600 лет назад, но это все «лирика». Проблема в том, что так вести расчеты, постулируя, что гаплотипы происходят от одного общего предка, вообще нельзя. Вот как выглядит ДНК-генеалогическое дерево этих 194 гаплотипов (рис 13.).

На дереве видны многочисленные ветви, в каждой из которых – свой общий предок. Нет и не может быть в такой ситуации некоего «одного общего предка», ветви нужно анализировать раздельно. Как было показано в наших работах, серия идентичных гаплотипов, идущих по кругу выше, имеют общего предка, который жил 1075±130 лет назад («академическая выборка») или 1050±190 лет назад («коммерческая выборка», то есть по коммерческим базам данных), что практически одно и то же, и разница между ними заметно проявляется уже в 67-маркерном формате гаплотипов.

Какой вывод из этого следует? Тот, что нельзя проводить расчеты по сериям гаплотипов «чохом», без разделения их на ветви. Нет ничего проще, чем выписать гаплотипы в серию, посчитать в них мутации от чего-то среднего, или от какого-то заранее заданного «предкового» гаплотипа, и разделить число мутаций на число гаплотипов и на скорость мутаций, которая нравится, или почему-то принимается. Какое-то число при этом всегда получится. Но это будет, как правило, мусор, с претензией на «научность». Популяционные генетики заполняют подобным мусором академические журналы на протяжении последних 20 лет. Никакого смысла в этих «расчетах» нет.

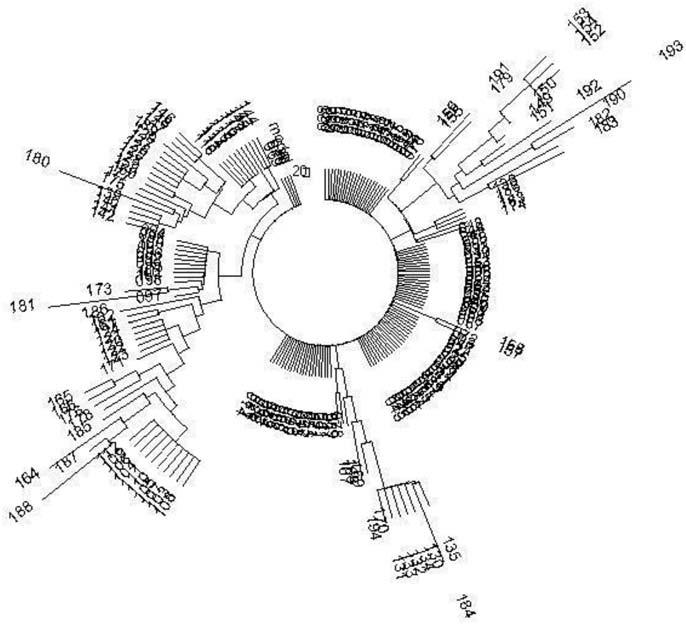
Рис. 13. Дерево 6-маркерных гаплотипов евреев гаплогруппы J, построено по данным Behar et al. (2003). В выборке – 194 гаплотипа.

Но как узнать, рассматриваемая серия гаплотипов «однородная», от одного общего предка, или разнородная, от разных общих предков, и дальнейшие расчеты в таком виде бессмысленны? Это – важный, и даже важнейший вопрос, который в ДНК-генеалогии решается двумя путями – графическим и аналитическим. Графический метод – это постройка дерева гаплотипов и его рассмотрение, симметричное ли дерево, или состоит из различных ветвей. Если симметричное (примеры даны ниже), то можно применять простые метода расчета, как линейный или с помощью калькулятора Килина-Клёсова. Если дерево состоит из четко разделяющихся ветвей, как на рис. 13, то расчеты (линейный или калькуляторный) следует проводить по каждой ветви раздельно.

Аналитический метод – это применение логарифмического метода анализа гаплотипов, и полученный результат (число лет до общего предка) сравнивается с результатом линейного расчетного метода, применяемого «чохом», ко всей серии гаплотипов. Если результаты различаются (пример дан ниже), то серия гаплотипов неоднородна, и надо переходить к графическому методу разделения ветвей, как описано выше.

Например, в ситуации с 194 гаплотипами евреев гаплогруппы J (рис. 13), линейный метод («чохом») дает 263/194/0.0074, и получается 5600±660 лет до общего предка «гаплотипов коэнов». Логарифмический метод дает [ln(194/91)/0.0074] = 102 ? 114 условных поколений, или 2850±410 лет до общего предка. Результаты совершенно разные, значит, ни тот ни другой метод не подходят. Собственно, это и показывает рис. 13.

Вот этого попгенетики никогда не могли усвоить.

Вопрос 72: Можно несколько подробнее о линейном методе расчета?

Как было неоднократно объяснено выше, линейный метод – самый простой при вычислении времени, прошедшего от общего предка данной серии гаплотипов. Поскольку чем больше это время, тем больше мутаций накопилось в гаплотипах потомков общего предка, и мутации в гаплотипах накапливаются в основном неупорядоченно, то к расчетам применима простая формула:

n/N = kt,

где n – число мутаций в серии гаплотипов, N – число гаплотипов в серии, k – константа скорости мутации, t – время до ближайшего общего предка.

Пояснения: (1) число мутаций считается от базового гаплотипа, который или является предковым, или максимально к нему приближен, насколько позволяет подборка гаплотипов, (2) отношение числа мутаций к числу гаплотипов определяет произведение kt, которое выражается в числе мутаций; как видно, константа в таких формулах всегда связана со временем до общего предка, (3) время до общего предка обычно определяют в условных поколениях протяженностью 25 лет, и тогда константа скорости мутациях определяется в числе мутаций на условное поколение протяженностью в 25 лет. Как видно, извечный вопрос попгенетиков о том, какую протяженность поколения использовать в расчетах, лишен смысла, поскольку какую протяженность мы бы ни брали, она входит в величину константы скорости мутаций, и итоговая величина kt остается той же, равной отношению n/N. А это – независимая переменная, она задается серией гаплотипов, то есть независимой выборкой. «Независимой» здесь означает, что гаплотипы для выборки не подбираются по усмотрению исследователя, они выбираются неупорядоченно.

Пример: имеются 275 111-маркерных гаплотипов гаплогруппы N1C1. В них суммарно имеются 6270 мутаций. Общий предок жил 6270/275/0.198 = 115 ? 130 условных поколения, или 3250±330 лет назад (округленно). Калькулятор Килина-Клёсова дал 3233±326 лет назад.

Поправка на возвратные мутации производится или по специальным таблицам[82], [83], или по формуле, приведенной в этой книге выше[84].

Вопрос 73: Можно подробнее о квадратичном (пермутационном) методе, и расчете погрешностей при его использовании?

Квадратичный метод, в отличие от линейного, есть в двух основных вариантах – с использованием базового гаплотипа и без ориентации на базовый гаплотип. В первом случае считаются не мутации от базового гаплотипа, а квадраты мутаций. Например, в серии из трех 12-маркерных гаплотипов

13 24 16 10 11 15 12 12 10 13 11 30

13 25 16 11 11 15 12 12 10 13 11 30

13 24 16 11 11 15 12 12 11 13 11 30

с базовым гаплотипом

13 24 16 11 11 15 12 12 10 13 11 30

и тремя мутациями от базового гаплотипа (выделены), линейный метод дает 3/3/0.02 = 50 ? 53 условных поколения, то есть 1325±780 лет до общего предка. Столь большая погрешность вызвана малым числом гаплотипов в серии, причем гаплотипов коротких, и малым числом мутаций. Напомню, что расчет погрешности в данном случае проводится извлечением квадратного корня из трех (мутаций), что дает 1.732, далее его обратной величины (1/1.732 = 0.577), возведением ее в квадрат (0.577² = 0.333), прибавлением 0.01 (это – квадрат принятой погрешности величины константы скорости мутации, которая принимается равной ±10 %, то есть ±0.1), что дает 0.343, и, наконец, извлечением квадратного корня из последней величины, что дает 0.586 (то есть ±58.6 %). Это и есть величина погрешности определения времени до общего предка при трех мутациях в серии гаплотипов. При величине 1325 лет погрешность равна 1325x0.586, то есть ±780 лет.

Надо сказать, что в описанном (упрощенном) варианте есть много допущений. Допущения есть всегда, в любом варианте расчета погрешностей. Например, в данном случае мы принимаем, что погрешность определения константы скорости мутации в 12-маркерных гаплотипах (ее величина равна 0.02 мутаций на гаплотип на условное поколение) составляет ±10 %. Это – эмпирическая величина, полученная при изучении серии данных документальной генеалогии. Такую же погрешность мы принимаем и в случае 67-маркерных гаплотипов, хотя сопоставление ДНК-генеалогических данных с многочисленными данными документальной генеалогии показало, что реальная погрешность равна ±3 %, и в этом случае в примере выше к величине 0.333 следует прибавлять не 0.01, а 0.0009, и итоговая погрешность получится не ±58.6 %, а 57.8 %, что практически одно и то же. Это получается, потому что при всего трех мутациях именно столь малое их число практически полностью определяет погрешность времени до общего предка серии гаплотипов. Только при большом числе гаплотипов и большом числе мутаций общую погрешность начинает определять погрешность определения константы скорости мутаций. Например, при 1000 мутаций в серии гаплотипов погрешность вычисляется, как описано выше, извлечением квадратного корня из 1000 (мутаций), что дает 31.62, далее его обратной величины (0.0316), возведением ее в квадрат (0.001), прибавлением 0.01 (при 10 % погрешности величины константы скорости мутации), что дает 0.011, и, наконец, извлечением квадратного корня из последней величины, что дает 0.105 (то есть ±10.5 %). Это и есть величина погрешности определения времени до общего предка при 1000 мутациях в серии гаплотипов. При величине 1325 лет погрешность тогда равна 1325±140 лет. А если погрешность константы скорости мутаций равна ±3 %, то к величине 0.001 (после возведения в квадрат) следует прибавить не 0.01, а 0.0009, и итоговая погрешность получится не 10.5 %, а 4.4 %, или 1324±60 лет до общего предка.

Но мы предпочитаем иметь преувеличенную погрешность, чем даже реальную, потому что это повышает доверие к получаемым результатам. Бывает, что число мутаций в реальных генеалогиях по разным причинам оказывается заниженным или завышенным по сравнению со средними величинами, и расчетная величина вылетает за пределы указанных погрешностей, вызывая недоверие и претензии к расчетам. Пусть лучше мы перестрахуемся и дадим завышенные погрешности.

Возвращаемся к квадратичным методам расчетов. В данном случае базовый гаплотип не рассматривается, и производится расчет разницы в аллелях «всех между всеми». В случае приведенных выше трех 12-маркерных гаплотипов с тремя мутациями сумма квадратов их попарных отклонений друг от друга (в мутированных маркерах) равна 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² = 12, деленная на 2, поскольку в каждом маркере число квадратов мутаций считалось дважды, деленное на число маркеров в гаплотипе (12) и на квадрат числа гаплотипов (9), и, наконец, на величину константы скорости мутации на маркер для 12-маркерных гаплотипов (0.00167). Получаем 12/2/12/9/0.00167 = 33 условных поколений, то есть 825±480 лет до общего предка. В квадратичных методах расчетов поправка на возвратные мутации не вводится, она уже учтена самим методом расчета.

Как видим, мы имеем некоторую проблему. Линейный метод показал для этих трех гаплотипов с тремя мутациями 1325±780 лет до общего предка, квадратичный метод – 825±480 лет до общего предка. В принципе, обе величины находятся в пределах погрешности расчетов, но утешение от этого малое. Причина проста – три мутации на трех гаплотипах – это не статистика. Методы, описанные выше, базируются на статистическом распределении аллелей и мутаций в гаплотипах. Аналогия – если вы бросите монету три раза, или четыре для четности, то вероятность получения 50 %-ного выпадения орла и решки будет малой. Давайте попробуем для иллюстрации. Буду использовать компьютерные «броски» для объективности. Итак,

– первая четверка бросков, все четыре орла

– вторая попытка, решка и три орла

– третья попытка, решка и три орла

– четвертая попытка, три решки и орел

– пятая попытка, решка и три орла

– шестая попытка, две решки и два орла

– седьмая попытка, три решки и орел

– восьмая попытка, две решки и два орла

– девятая попытка, три решки и орел

– десятая попытка, решка и три орла

Результат налицо – из десятка попыток по четыре броска, только два раза выпали две решки и два орла. В целом же из сорока бросков 17 раз выпала решка, и 23 раза орел. Ну как, будем считать вероятность выпадания того или другого? Или здравый смысл остановит такие расчеты? Кстати, с доверительным интервалом в две сигма (95 %) решка и орел выпадут из сорока бросков 20±6 раз для решки, и 20±6 раз для орла, так что никакого противоречия у нашего опыта со статистикой нет. А из четырех бросков получится 2±2 для решки и 2±2 раза для орла. Тоже все в порядке, никаких неожиданностей.

А люди берут три-четыре коротких гаплотипа, а то и два, и удивляются, почему результаты «бегают по всему полю».

Вопрос 74: Автоматический калькулятор Килина-Клёсова

Давайте теперь проверим, какой результат ближе к реальности в случае трех коротких гаплотипов, рассмотренных выше – расчет по линейному методу (1325±780 лет до общего предка) или квадратичному (825±480 лет до общего предка). Кликаем на линк, ведущий к калькулятору Килина-Клёсова[85] на сайте http://dna-academy.ru/kilm-klyosov/, вводим все три серии аллелей под соответствующими маркерами, и через долю секунды получаем результат – 1304±764 лет до общего предка линейным методом и 863±456 лет – квадратичным.

Мы видим, что при столь малом числе гаплотипов и мутаций датировки нестабильны. Но в такой ситуации я бы рекомендовал склоняться к линейному методу, поскольку расчет по трем аллелям, пусть и для 12 маркеров, вряд ли является удовлетворительным. Но еще лучше – просто давать обе датировки, поясняя, какая получена каким методом.

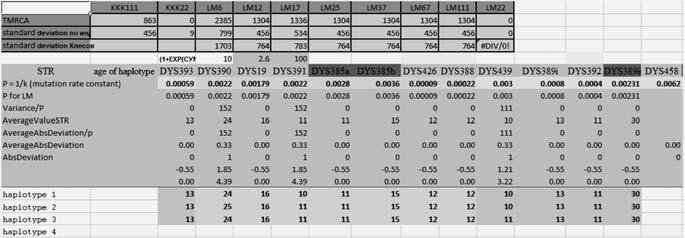
Рис. 14. Расчет времени до общего предка для демонстрационной серии из трех гаплотипов в 12-маркерном формате на калькуляторе Килина-Клёсова. Соответствующие колонки показывают 1304±764 лет до общего предка для линейного метода, и 863±456 лет для квадратичного метода, что, впрочем, совпадает в пределах погрешности расчетов. Остальными колонками следует пренебречь.

Как работает калькулятор Килина-Клёсова? Он многофункциональный, и здесь нет возможности объяснять все его функции, кроме основной – быстро производить расчеты по гаплотипам от любых коротких (вплоть до единичных, отдельных маркеров) до 111-маркерных, в количествах до 10 тысяч гаплотипов. Калькулятор моментально, в ходе расчетов, определяет степень диперсии аллелей по каждому маркеру, и показывает ее количественную величину. Можно выставлять пороговую величину степени дисперсии, тогда калькулятор выбрасывает соответствующие маркеры из расчетов. Это особенно полезно, когда серия гаплотипов содержит включения посторонних гаплотипов, или нижестоящих субкладов, у которых некоторые маркеры имеют другие значения, чем у основной серии. Например, в серии гаплотипов гаплогруппы R1a значение маркера DYS392 обычно имеет величину 11, а в отдельной ветви «Старая европейская ветвь» это значение равно в основном (или исключительно) 13. Калькулятор «знает», что маркер DYS392 настолько «медленный» (константа скорости мутации равна 0.0004 мутаций на маркер на условное поколение), что, например, для тысячи гаплотипов в среднем должно наблюдаться примерно 40 мутаций за сто условных поколений, потому что 40/1000/0.0004 =100 условных поколений. При увеличении количества аллелей DYS393=13 в серии гаплотипов, дисперсия возрастает и в итоге превышает граничную величину 2.6, обычно используемую при расчетах. При величине 2.61 маркер блокируется, оставляя все остальные – незаблокированные – функциональными. Если в рассматриваемой серии гаплотипов блокируются сразу несколько маркеров, то это указание на то, что что-то с выборкой не так.

Поправка на возвратные мутации в калькуляторе не вводится, она уже заложена в самом калькуляторе, как для линейного метода, так и квадратичного. Калькулятор на 111 маркеров может использоваться для расчетов гаплотипов в любом формате, включая 67-маркерные, но для удобства нами создана серия калькуляторов для 17-маркерных и для самых медленных, 22-маркерных гаплотипов.

Калькулятор может быть использован для комбинаций серий гаплотипов для любых форматов. Это возможно потому, что в квадратичном методе он считает «по вертикали», по маркерам, а в линейном – «по горизонтали», по гаплотипам.

Вопрос 75: Поясните, пожалуйста, суть логарифмического метода в ДНК-генеалогии.

Логарифмический метод – самый простой в исполнении. Несколько примеров расчетов логарифмическим методом были даны выше. Суть его заключается в том, что для серии гаплотипов берется отношение общего числа гаплотипов в серии к числу идентичных (базовых) гаплотипов в той же серии, далее берется натуральный логарифм этого отношения, и делится на константу скорости мутации в данном гаплотипе. После этого вводится поправка на возвратные мутации, поскольку они возвращают мутированные гаплотипы обратно в исходные немутированные, и тем самым занижают датировку времени жизни общего предка. Поправка на возвратные мутации рссчитывается исходя из числа базовых гаплотипов в серии.

Чем больше по численности серия гаплотипов, происходящих от одного предка, тем расчет времени до этого предка точнее. И тем больше экономия времени при расчетах, поскольку логарифмический метод не требует подсчета числа мутаций в гаплотипах. Например, если серия из сотни гаплотипов, скажем, 37-маркерных, содержит четыре одинаковых (то есть базовых) гаплотипа, то даже и без подсчета мутаций в гаплотипах можно сразу сказать, что общий предок этих ста гаплотипов жил 925±105 лет назад, потому что натуральный логарифм отношения 100/4, поделенный на константу скорости мутации для 37-маркерных гаплотипов (0.09 мутаций на гаплотип на условное поколение в 25 лет) равен 36 ? 37 условных поколений, то есть общий предок этой сотни гаплотипов жил примерно 925 лет назад. Поскольку для четырех базовых гаплотипов погрешность расчетов составляет ±51 % (как это расчитывается – приводилось выше на примере четырех мутаций в серии гаплотипов), то общий предок для данной серии из ста гаплотипов жил 925±470 лет назад. Но, как уже обсуждалось выше, в любом случае, в том числе и в искаженных, неоднородных сериях, почти всегда можно найти одинаковые гаплотипы, и деление общего числа гаплотипов на случайное количество одинаковых гаплотипов всегда даст какое-то число, часто не имеющее отношения к числу лет или поколений до общего предка. Поэтому необходим критерий, что расчетные величины времен до общего предка действительно имеют смысл, и что серия гаплотипов действительно происходит от одного общего предка.

Этим критерием является совпадение (в пределах погрешности расчетов) времени до общего предка, рассчитанное как линейным (или квадратичным), так и логарифмическим методами. Например, если число мутаций во всех ста 37-маркерных гаплотипах будет равно, например, 324 (или близко к тому), тогда 324/100/0.09 = 36 ? 37 условных поколений, то есть ровно тот же промежуток времени до общего предка. Совпадение времен до общего предка для «логарифмического» и «линейного» метода (в первом мутации не считаются, во втором считаются) свидетельствует, что закономерности образования мутаций в гаплотипах следуют кинетике первого порядка, что в свою очередь означает, что все сто гаплотипов действительно произошли от одного прямого общего предка. Популяционная генетика такими подходами не пользуется, они ей чужды по ряду причин, как обсуждалось выше.

Вопрос 76: На каком основании некоторые популяционные генетики критикуют логарифмический метод?

Во-первых, это не «некоторые популяционные генетики», а один Балановский. Во-вторых, это не «критика», а смех один. Характерно, что он, при полном, как правило, отсутствии культуры расчетов, нападает не только на логарифмический метод, но и на всё остальное в ДНК-генеалогии. Забавно наблюдать эту выраженную ущербность «нападающего». Вот, например, цитата из моей недавней статьи на Переформате[86]: «В ДНК-генеалогии есть логарифмический метод… И он вовсе не «неточный», как безграмотно заявил О. Балановский, в очередной раз показав свою некомпетентность. Неточным любой метод бывает тогда, когда используется неправильно. Неточным будет микроскоп, если его использовать для рассматривания звезд. На то есть телескоп, или хотя бы подзорная труба.

Чем больше по численности серия гаплотипов, происходящих от одного предка, тем расчет времени жизни этого предка точнее. И тем больше экономия времени при расчетах, поскольку логарифмический метод не требует подсчета числа мутаций в гаплотиипах. Например, из 3466 12-маркерных гаплотипов субклада R1b-L21 249 гаплотипов являются базовыми, то есть идентичными друг другу. Это дает [ln(3466/249)]/0.02 = 132 ? 152 условных поколений, или 3800±450 лет до общего предка. Расчет по мутациям для этой же серии гаплотипов 3841±384 лет по 67-маркерным гаплотипам и 3810±381 лет по 111-маркерным гаплотипам. Разницы между логарифмическим и линейным (то есть по мутациям) методами расчета практически нет, на уровне сотых долей процента, хотя погрешность расчетов ее увеличивает.

Ну, и где здесь «неточный» логарифмический метод? И это говорит тот, ошибки у которого в расчетах датировок систематически равны как минимум 250–350 %».

Уж как Балановскому не нравится логарифмический метод! Он уже стал для Балановского идеей-фикс. Недавно Балановский объявил, что метод настолько «неточный», что я от него сам отказался… Казалось бы, откуда такая зацикленность на методе, который к нему, Балановскому, никакого отношения не имеет? Который он никогда не применял, видимо, потому, что не знает, что такое логарифм. А ответ прост – это злоба середнячка на что угодно новое, оригинальное, прогрессивное.

Еще цитата на ту же тему: Балановский объявил, что «технические методы «ДНК-генеалогии» вовсе не оригинальны, представляя собой обычный метод молекулярных часов с рядом простейших модификаций…С его точки зрения, технические аспекты «ДНК-генеалогии» являются «малоэффективными, но приемлемыми»…».

«С «молекулярными часами» мы уже разобрались. На что ни пойдет безграмотный человек, чтобы дискредитировать грамотного… пустится во все тяжкие, включая и свой позор на публике. Так что же такое «ряд простейших модификаций»? Введение впервые в оборот серии констант скоростей мутаций, нигде и никогда раньше не публиковавшихся? Введение в оборот логарифмического метода, совершенно незнакомого ранее попгенетикам? Введение в оборот поправок на возвратные мутации, о которых попгенетики говорили, но никто и никогда не рассчитывал и не применял? Введение в оборот калибровок констант скоростей мутаций?

Не знаю как для кого, а для меня ясно, что О. Балановский, будучи «на автопилоте» желания дискредитировать, себя уже не контролировал. Он что-то произносил, главное, чтобы было негативное, но смысла сам не понимал. Это – не наука, это и есть лженаука в исполнении О. Балановского, как и другого доктора, Е. Балановской.

Самое забавное в том, что этот незнайка, применяя «методы» популяционной генетики и ошибаясь на сотни процентов в датировках, заявляет, что «технические аспекты «ДНК-генеалогии» являются «малоэффективными, но приемлемыми»…». «Малоэффективные» произнесено на том же автопилоте, в том же раже дискредитировать. Если бы его спросили расшифровать понятие «малоэффективные», он бы не нашел, что ответить. Ни одного примера привести бы не смог. За «приемлемые» – отдельное спасибо, мой сарказм заметен?»

На конференции в РАН в ноябре 2014 года О. Балановский показал следущий слайд:

Я привел его на Переформате[87] и прокомментировал: «Это какие же «многие методы датировок» известны в популяционной генетике? Что такое «неоптимальная логарифмическая формула»? Что за «калибровка, совпавшая с уже известной»? Опять сплошная ложь. Возможно (и определенно) полная некомпетенция, безграмотность. Ранее я показывал, что за «методы датировок» используют в попгенетике, и к чем это приводит. К мусору, которым заполняют журналы…»

Давайте напрямую. Никаких «многих методов» в популяционной генетике нет. Иначе бы не выбрали печально известный «популяционный метод», который системно дает завышения датировок на 300–350 %, и который с 2004 года узаконен в академических журналах популяционной генетики и применять который продолжают требовать рецензенты. «Неоптимальная» логарифмическая формула – это основное уравнение химической кинетики для процессов первого порядка, которое адаптировано к расчетам кинетики мутаций в гаплотипах, включая поправку на возвратные мутации. «Калибровки, совпавшей с уже известной» просто нет, это просто выдумано, просто для пустого негатива.

Остается с жалостью наблюдать, как Балановские выдумывают все что угодно, лишь бы «дискредитировать», как им представляется, новые подходы, им до того неведомые.

Балановским вторит некто «Алекс» в дискуссии на «Троицком варианте»[88]: «почему «линейный» и «логарифмический» методы названы независимыми? И общее число мутаций, и число немутировавших гаплотипов определяются временем и скоростью мутирования, так что вычисленное по ним время не может не быть одинаковым».

Я ответил: «То, что «вычисленное по ним время не может не быть одинаковым» – принципиальное непонимание того, что серии гаплотипов очень часто представляют собой смеси разного происхождения. Собрали в некоем регионе пару сотен гаплотипов, а откуда известно, что они от одного общего предка? Без этого «расчет времени до ближайшего общего предка» не имеет смысла, хотя представляется заманчивым просто посчитать у всех число мутаций и разделить на число гаплотипов. Какое-то число всегда получится. А вот если применить упомянутые два расчетных подхода, то они часто дают разные величины. Это и означает, что смесь гаплотипов «неоднородна», картина мутаций не подчиняется закономерностям кинетики первого порядка. Только если оба метода дали одинаковые результаты (в пределах погрешности расчетов), то результат верен.

Аналогия – попытка рассчитать «время полураспада» смеси разных радиоактивных материалов. Система не будет описываться кинетикой первого порядка (кроме совсем уж специальных случаев, когда у всех материалов одно и то же время полураспада).

Как часто бывает, люди безграмотные, типа Балановского или «Алекса», генерируют общий негативный шум, причем совершенно неконструктивный. Никто из них не сообщил, как надо рассчитывать, и почему логарифмический метод «неоптимальный». Что такое вообще «оптимальный»? Может, Балановский сообщит, даст пример «оптимального»? Понятно, что нет, он в подобных расчетах совершенно тёмный человек. Но ужас как хочется «критиковать», «подвергать сомнению», авось, кто нибудь, столь же темный, клюнет. Нет ничего более далекого от науки, хотя Балановский к науке имеет совершенно косвенное отношение. Это, скорее, лаборант от науки, как и Е. Балановская. Никакой научной критики от них никогда не было, были только общие инсинуации, к науке не имеющие отношения. Например, Е. Балановская с трибуны той же ноябрьской конференции в РАН оповестила: «Клёсов эксплуатирует собранную генетиками информацию, обрабатывает её неизвестными методами и получает красивые результаты на потребу публике». Так все-таки неизвестными методами, или «известными в популяционной генетике»? Мать и дитя Балановские уже настолько изолгались, что сами себе противоречат. Если действительно «неизвестными методами», и попгенетики настолько беспомощны в корректной и информативной обработке собранных ими гаплотипов, то надо заменить их некомпетентность и неумение на полученные корректными методами «красивые результаты», тут Балановская не ошиблась. А что до «неизвестных методов», то учиться надо. И придется учиться, деваться просто некуда. А уж «на потребу публике» – это ложь Балановской от беспомощности и отчаяния, от своей некомпетентности. Красивые результаты – это правильные результаты, что еще физики давно подметили.

Почему попгенетики переполошились в отношении логарифмического метода датировок общих предков выборок гаплотипов?

Забавно наблюдать переполох в стане попгенетиков, который (переполох) у них вызвал логарифмический метод. Давате рассмотрим причины этого явления, но так, чтобы это продвинуло наши знания. Характерно, что попгенетики своей «критикой» знания не продвигают, у них обычно голый и непродуктивный негативизм. Мы уже отметили выше безграмотные и неконструктивные высказывания Балановского, что логарифмический метод, по его мнению, «неоптимальный», и некого «Алекса», что этот метод ничего не дает, поскольку он, как и все остальные, определяется «временем и скоростью мутирования», а, значит, ничего нового. Опять безграмотность зашкаливает. По этой логике, любые методы и расчетный аппарат химической кинетики ничего нового не дают, поскольку все они определяются временем и скоростями реакций. Представляете «глубину» вот такого высказывания? И генетика по этой логике ничего не дает, там вообще всего четырьмя нуклеотидами все определяется. Узнал, какими, и вся генетика уже как на ладони, ничего нового. И вот так, такими «специалистами», проводилась вся дискусия на «Троицком варианте».

Вопрос – откуда такое нестерпимое желание дискредитировать новые методы и их авторов? Ведь действительно забавно это наблюдать.

Прежде чем ответить на этот вопрос, рассмотрим, в чем состоит новизна и полезность логарифмического метода при анализе скоростей мутаций и расчетов времен жизни до общего предка выборок гаплотипов. Сразу скажем, что ничего подобного в попгенетике не было. Никто логарифмические методы в расчетах до последнего времени, до моих публикаций в 2009 году, не применял. Так что вопрос о новизне в применении к мутациям в гаплотипах решается просто и однозначно.

Теперь посмотрим, откуда этот метод появился. По сути, это хорошо известный подход в химической кинетике, описывающий кинетику первого порядка, правда, мутации в гаплотипах привнесли некоторые особенности. Никто не делает в химкинетике поправки на возвратные мутации, потому что процессы, описываемые кинетикой первого порядка, обычно являются необратимыми процессами, и описываются константой скорости первого порядка, в том числе и тогда, когда включают элементы обратимости. Просто в последнем случае реакция доходит не до конца, по типу A ? B, а до некоего равновесного процесса, при котором в системе «уравновешиваются» остатки химического соединения А и продукта его превращения В. Задачи обычно состоят в расчете константы скорости первого порядка, либо «элементарной», либо «кажущейся».

В ДНК-генеалогии ставится другая задача, а именно исходя из картины мутаций в серии гаплотипов, найти время, когда жил общий предок этой серии гаплотипов, которую имеют потомки. Там есть возвратные мутации, искажающие картину, и занижающие время до общего предка, поэтому там надо не рассчитать константу скорости мутации, она уже известна из других опытов, а найти время до общего предка, скорректированное на обратные мутации, причем корректировка зависит от того, когда жил общий предок выборки. Наверняка можно придумать аналогичную систему и в химической кинетике, но так вопрос обычно не ставится.

Тогда почему такая возня со стороны попгенетиков, с выраженным желанием отрицать значимость метода? Метод же очень удобный, для больших серий гаплотипов (где подсчет мутаций наиболее трудоемкий) задача решается буквально за минуту-две, вместо многих часов, а то и дней, на подсчеты тысяч мутаций, и что важно, он дает новый критерий однородности системы гаплотипов и, следовательно, корректности расчетов времени жизни общего предка. Предствляете, сколько нужно времени для подсчета числа мутаций в серии из 3466 гаплотипов в 111-маркерном формате, то есть в наборе из 384 726 аллелей, со временем жизни общего предка 3800 лет назад? Там – 92 120 мутаций. А логарифмическим методом – несколько минут. Берется файл в Excel, и используя известную функцию компьютера, аллели сортируются, выбирая только базовые гаплотипы. Это делается буквально в несколько касаний.

Иначе говоря, польза логарифмического метода в ДНК-генеалогии не только очевидна, она без преувеличений огромна. Так почему попгенетики так дергаются, изливая негативные комментарии? «Элементарно, доктор Ватсон». Одна причина – потому что попгенетики за двадцать лет так и не создали разумного метода расчетов времен жизни общих предков. Их результаты либо полностью неверны, либо кардинально противоречат друг другу. Приложения новых методов ДНК-генеалогии тут же покажет, что они всегда генерировали мусор. Статьи придется фактически дезавуировать, а за ними стоят гранты, диссертации…

Другая причина – банальная ревность, раздражение тем, что они так и не знают, как считать, а здесь «сторонний» специалист задачу решил. Ату его! И начинается – «лже-генетик» там, где никакой генетики нет, «провал ДНК-генеалогии в РАН», когда все наоборот – аплодисменты ДНК-генеалогии, а попгенетиков выгоняют из зала заседаний. После этого и их ставленники, типа некой «журналистки» Маркиной, строчат лживые пасквили в электронные СМИ, переворачивая там все с ног на голову. Об этом – ниже в этой книге.

Показательным в отношении логарифмического метода явилась форменная истерика на «дискуссии» в «Троицком варианте», которую начала Балановская, подписав свой авторский пасквиль, и продолжил Балановский. Там – больше десятка комментариев только о логарифмическом методе.

Взглянем на них, и поясним, к чему предъявляют претензии попгенетики и их приятели.

Начал претензии Балановский: «И уж простейший кинетикой первого порядка тут и не пахнет, порядок был бы скорее пятидесятый. А если речь идет просто о логарифмической формуле, которую Клесов взял из хим. кинетики и перенес в свою ДНК-генеалогию, то она позаимствована из формулы радиоактивного распада. Получается, в миграциях народов лучше всех должны разбираться ядерщики?

Можно спорить здесь только о том, чего больше в этом «комментарии» – откровенной глупости или полной безграмотности. Балановский, оказывается, так и не понимает, что мутации в гаплотипах и маркерах подчиняются именно кинетике первого порядка, в отношении «пятидесятого» тут уже буйное помешательство. Когда сами же попгенетики применяют печально известную «скорость Животовского», и делят число мутаций на число маркеров и на «популяционную скорость мутации» 0.00069, получая совершенно искаженное «время до общего предка», это тоже есть выражение кинетики первого порядка. Возможно, они (как и профессор Животовский), следуя известному герою пьесы Мольера, не подозревают, что говорят прозой, то есть отражением кинетики первого порядка.

Далее, нет никакой «формулы радиоактивного распада», если не считать «формулой» описание химического (или физического) превращения в ходе радиоактивного распада. Если же речи идет о кинетике первого порядка, то ни из какого «радиоактивного распада» она не «позаимствована». Кинетикой первого порядка описываются сотни и тысячи процессов, в том числе и процессы радиоактивного распада, только никаких аналогов «возвратных мутаций» при радиоактивном распаде нет. Они – необратимы. А уж последняя фраза, про «ядерщиков» – верх глупости. Хотя бы потому, что к миграциям народов кинетика первого порядка сама по себе никакого отношения не имеет. В народе это называется «Остапа несло». У Балановского – это «несло» привело к словесному недержанию в острой форме.

Далее – опять Балановский, про меня: «… излагает свой прием проверки того, можно ли рассчитывать возраст данного набора гаплотипов, используя логарифмическую формулу. Подход (сравнение результатов логарифмического и линейного методов) весьма топорен, формально он математически необоснован, но по сути вполне допустим.

Другое дело, что пользы от него немного. Он показывает, в каких случаях можно применять логарифмическую формулу. Но применять ее незачем. Валерий уже описывал подробно, что эта формула ничем не лучше стандартной «линейной».

И что же «топорного» в сравнении результатов логарифмического и линейного методов? Они приведены и сравнены выше, совпадение практически полное. Что здесь «математически необосновано»? И это говорит человек, который столько статей заполнил мусором в отношении расчетов, который датировку для субклада R1a-M458 вместо правильных 4200±350 лет назад (http://pereformat.ru/2015/03/veneti-2/) или 4500±800 лет назад (данные YFull, http://www.yfull.com/tree/R1a/), опубликовал как 10712±3914 лет назад – кстати, обратите внимание на бессмысленную точность «возраста» субклада при огромной погрешности[89], и это – окончательная датировка, которая пошла в статью. Ну, не лаборант ли он по стилю и по духу?

Математическое обоснование сопоставления логарифмического и линейного методов расчета я давал в научной печати много раз. Любая реакция в химических или биологических системах, описываемая константой скорости первого порядка, есть «обычные молекулярные часы», поскольку связана с хронологией процесса на молекулярном уровне. Динамика любого такого процесса связана с временем согласно формуле с = с_ое^-к1, где с_о – исходное состояние системы (например, начальное количество или концентрация изучаемого вещества; количество гаплотипов Y-хромосомы в изучаемой выборке, и т. д.), с – состояние системы в определенный момент времени t (где t – время прошедшее с начала реакции, t-t_o), или количество базовых, то есть исходных гаплотипов в изучаемой выборке в настоящее время, спустя время t, прошедшее со времени жизни общего предка изучаемой серии гаплотипов), к – константа скорости реакции (мутаций, в данном случае). Эту же формулу можно переписать в виде ln(c_o/c) = kt, и она становится выражением логарифмического метода анализа выборок гаплотипов в ДНК-генеалогии. Берем, скажем, сто или тысячу гаплотипов, или любое другое их число, делим на число базовых (то есть одинаковых, идентичных друг другу гаплотипов, суть предковых гаплотипов, которые не успели мутировать за время t, прошедшее со времени жизни общего предка), берем натуральный логарифм (ln), и получаем произведение kt, то есть константу скорости мутации, помноженную на число лет, прошедшее со времени жизни общего предка, или на число условных поколений, опять же прошедших после общего предка – в зависимости от того, выражали константу скорости в годах, или в поколениях.

Иначе говоря, и линейный, и логарифмический метод определяют время, прошедшее со времени жизни общего предка анализируемой выборки гаплотипов. Но Балановский даже простую математику не воспринимает, или просто прикидывается. Задача его ясна – «ниспровержение» любой ценой. Даже «ниспровержение» абсурдное, показывающая его собственную некомпетентность.

Продолжаем цитировать откровения Балановского: Подход (сравнение результатов логарифмического и линейного методов)… пользы от него немного. Он показывает, в каких случаях можно применять логарифмическую формулу. Но применять ее незачем. Валерий уже описывал подробно, что эта формула ничем не лучше стандартной «линейной».

Опять патологическое невосприятие науки Балановским. Сравнение результатов логарифмического и линейного методов показывает не только, «в каких случаях можно применять логарифмическую формулу». Он совершенно симметрично показывает, в каких случаях можно применять линейный метод. Как рассказывалось выше, если результаты линейного и логарифмического метода заметно различаются, то кинетика накопления мутаций в выборке не подчиняется закономерностям первого порядка, и выборка гаплотипов «кривая». У нее несколько общих предков, и расчет в предположении только одного ведет к принципиально неверным результатам. Поэтому то, что «Валерий» Запорожченко, тоже малограмотный попгенетик, «описывал подробно, что (логарифмическая) формула ничем не лучше стандартной «линейной», тоже указывает на его фундаментальное непонимание азов анализа мутаций в гаплотипах. Логарифмический подход не может расматриваться в терминах «лучше» или «хуже» линейного, они друг друга дополняют, и должны применяться вместе там, где это возможно, или где нужно проверить, происходит ли выборка от одного общего предка. Есть много разных ситуаций – много гаплотипов в выборке или мало, протяженные гаплотипы или короткие, древний общий предок или относительно недавний, и для каждой ситуации тот или иной метод является более или менее предпочтительным. Поэтому «применять ее (логарифмическую формулу) незачем» – это опять вопиющая безграмотность Балановского и Запорожченко, непонимание ими азов расчетного аппарата ДНК-генеалогии, ревность середнячков в науке по отношению к тем, кто знают и понимают больше них. Ущербность, одним словом. Не должен настолько безграмотный Балановский работать в академической системе, и, надеюсь, это будет услышано теми, кто «принимают решения».

Продолжаем, опять Балановский, и опять про логарифмический метод, описывая, как рассчитать время до общего предка: «Расчет числа мутаций от условно реконструированного предкового гаплотипа – например, ASD-статистика (БендирЬа et al, 2006), суда же относится и логарифмический метод Кле-сова».

Опять Балановский ничего не понял. Нет в логарифмическом методе «расчета числа мутаций», там мутации вообще не считаются, и тем более от «реконструированного предкового гаплотипа». Ничего «реконструированного» в логарифмическом методе нет, там базовый гаплотип наблюдается напрямую, и число его повторов вносится в логарифмическую формулу. Не странно ли, что Балановский, не имея понятия, о чем говорит, все время ударяет лицом в грязь? Неужели ему не надоело и не совестно? Хотя опыт показывает, что нет, не надоело и совсем не совестно.

В дискуссию опять вступает некий «Alex», который опять сомневается в логарифмическом методе расчетов, в частности, в использовании понятия «число поколений» – «Какой же смысл имеет это число поколений, если базовый гаплотип – не настоящий предковый». Ну, «Алексу» простительно, он время от времени сообщает, что не разбирается ни в генетике, ни в ДНК-генеалогии. Правда, зачем-то комментирует. На самом деле в логарифмическом методе базовый гаплотип – это именно предковый. В примерах выше мы приводили реальные данные – в одной выборке гаплотипов было 249 базовых гаплотипов, в другой – 114, в третьей – 88 базовых гаплотипов. Это те гаплотипы, которые были идентичны друг другу в выборке. Чем ближе общий предок выборки жил к нашему времени, тем больше пропорция базовых гаплотипов в выборке. Никакой «реконструкции» базовых гаплотипов там не требуется, они – непосредственно предковые.

Слово получает Валерий Запорожченко, попгенетик, ученой степени нет: «логарифмический способ нам показывает дистанцию между КАКИМ-ТО гаплотипом в выборке, и всеми прочими гаплотипами в ней». Я, признаться, не знаю, как можно так исказить смысл логарифмического метода. Еще раз – в выборке находится серия базовых гаплотипов, это те, которые в выборке повторяются несколько или много раз, и это число подставляется в логарифмическую формулу, приведенную выше. Примеры расчетов даны выше. Как можно при этом писать, что «логарифмический способ нам показывает дистанцию между КАКИМ-ТО гаплотипом в выборке, и всеми прочими гаплотипами в ней»? Не «какой-то» гаплотип, а тот, который в данном случае повторяется, в рассмотренном выше примере, 249 раз.

Еще комментарий, каким-то участником «без лица», что «в логарифмическом методе идет «простое вымывание базового гаплотипа»

Я прокомментировал: это относится к любому процессу в химии или биохимии, там или «простое вымывание» исходного материала, или «простое накопление» продукта. В радиохимии идет «простое вымывание» исходного изотопа. А когда есть смесь изотопов, то идет «простое вымывание» их всех, одних быстрее других, других медленнее. Мудро. Осталось только кинетику процесса посчитать. Да на вклад отдельных изотопов (или гаплотипов) разделить. Да поправку на возвратные мутации (в гаплотипах) внести. Да решить, какие маркеры для расчетов использовать. Да константы скоростей мутации откалибровать по генеалогиям и историческим событиям. То-то попгенетики уже 20 лет с этим «простым вымыванием» справиться не могут.

Уже на склоне «дискуссии» некто Сергей воскликнул: «Клёсову по существу кто-нибудь будет возражать содержательно? Возьмём его логарифмическую формулу, что в ней неправильно?». Ответа ни от кого не последовало.

Alexei Kassian – лингвист, «подписант» письма 24-х: «для Клесова генеалогия МакДональдов – это и есть основная калибровочная шкала, по которой он выкручивает свою логарифмическую формулу».

На это я и отвечать не стал. Касьян и понятия не имеет, о чем пишет. И при таком «понятии» он подписывает коллективное письмо против ДНК-генеалогии. Про ДНК-генеалогию МакДоналдов я расскажу при ответе на следующий вопрос.

Вообще в таких «дискуссиях» в очередной раз понимаешь их бессмысленность. Дискуссия хороша там, когда стороны внимательны по отношению друг к другу, хотят понять, в чем они могут ошибаться, и хотят найти «истину» в той мере, в какой она имеет место (или может быть воспринята как наименее противоречивая концепция) на данном этапе научного познания. В «Троицком варианте» такого не было и близко. Никакие объяснения заблуждений попгенетиков и прочих историков (типичный пример – Л. Клейн) в принципе ими не воспринимались, да вопрос ими так и не ставился. Даже такой «прозрачный» пример, как логарифмический подход расчета в сериях гаплотипов, отвергался с самого начала, и объяснения были бесполезными. Они либо игнорировались, либо отвергались на смехотворной основе, либо «дискуссия» переходила на личности. Время от времени в «дискуссию» внедрялись люди, от науки вообще бесконечно далекие, типа «журналиста» В. Лебедева, и вбрасывали полностью лживую информацию персональной направленности, типа что мной занимаются судебные органы США за финансовые махинации, или что я планирую получить часть наследства русского царя Николая Второго. Никаких источников, естественно, при этом не приводилось, и приводиться не могло. Лебедев вообще типичный представитель желтой прессы, патологический лжец и русофоб, и понятно, что я его раздражаю за происхождение из среды древнего военно-боевого состава (Лебедев своих предков не знает даже в двух поколениях, да и в одном не очень осведомлен, о причинах не буду говорить), за антинорманистскую позицию (Лебедев – активный норманист), и так далее. Если бы я стал оспаривать эти лживые пасквили, тут же было бы объявлено, что я «оправдываюсь». Поэтому подобные дискуссии никакого смысла не имеют, кроме одного – их можно описать, текстуально процитировать «возражения» и дать им детальные объяснения для интересующихся читателей, что я и делаю.

Вопрос 77: Чем полезны сочетания документальной генеалогии и ДНК-генеалогии? Расскажите про пример МакДоналдов.

Пример с МакДоналдами показателен, так как с него фактически начиналась ДНК-генеалогия. Это были в свое время, семь лет назад, простые подходы, но они закладывали концептуальные подходы ДНК-генеалогии.

В Шотландии есть знаменитая «генеалогическая» семья МакДоналдов, их несколько тысяч человек, на них работает целый штат профессиональных генеалогов, их документальная генеалогия изучена во всех возможных деталях. И неудивительно, часть их (гаплогруппы R1a) берут свое начало от шотландского вождя Сомерледа, среди их предков наполеоновский маршал МакДоналд и много других выдающихся людей. Основная группа МакДоналдов гаплогруппы R1a ведет свою линию от Джона Лорда Островов (John Lord of the Isles), умершего в 1386 году, то есть 628 лет назад. Принимая 25 лет на условное поколение (именно эта величина входит в величины констант скоростей мутаций, приведенные в этой книге), получаем, что Джон умер 25 условных поколений назад, то есть жил примерно 25-26-27 условных поколений назад. В 2008 году серия гаплотипов потомков Джона[90] насчитывала 68 гаплотипов, затем (в 2010 году) 84 гаплотипа. Среди 68 гаплотипов в 6-маркерном виде было 17 мутаций, и 53 гаплотипа были немутированными, то есть базовыми. Начнем считать по правилам ДНК-генеалогии, сначала по мутациям, используя так называемый линейный метод: 17/68/0.0074 = 34±9 условных поколений до Джона (погрешность велика, поскольку мутаций мало). Теперь считаем без учета мутаций, используя логарифмический метод: [ln(68/53)]/0.0074 = 34±6 условных поколений назад. 0.0074 – это константа скорости мутаций для 6-маркерных гаплотипов, см. выше.

Потом появились 60 гаплотипов в 25-маркерном формате, в них – 69 мутаций, и из них 18 гаплотипов были базовыми, то есть идентичными друг другу. Получаем:

Линейный метод – 69/60/0.046 = 25±4 условных поколений.

Логарифмический метод – [ln(60/18)]/0.046 = 26±7 условных поколений.

Потом, с расширением тестирования, появились 84 гаплотипов в 25-маркерном фоормате, и в них во всех содержалось 109 мутаций. В тех же 84 гаплотипах в 12-маркерном формате было 44 мутации. Получаем:

Для 12-маркерных гаплотипов 44/84/0.02 = 26±5 условных поколений.

Для 25-маркерных гаплотипов 109/84/0.046 = 28±4 условных поколений. Здесь 0.02 и 0.046 – это константы скорости мутации для 12– и 25-маркерных гаплотипов, соответственно.

Мы видим, что по 6-маркерным гаплотипам идет завышение датировок, хотя и в пределах диапазона погрешностей. Но 6-маркерные – наименее надежные гаплотипы для расчетов датировок.

Итак, наблюдается разумное совпадение с документальной генеалогией по Джону и его потомкам: документальная генеалогия дает 628 лет до годовщины смерти Джона (1386 год), а ДНК-генеалогия дает 650–700 лет до времени его жизни (1314–1364 год), то есть практически абсолютное совпадение в контексте данного исследования, учитывая, что год его рождения неизвестен.

И таких примеров десятки, если не сотни, когда ДНК-генеалогия дает либо совпадения с документальной генеалогией (в пределах погрешности расчетов), либо дополняет документальную генеалогию, когда ее данные фрагментарные или вовсе отсутствуют, кроме приблизительных датировок.

Вопрос 78: Насколько надежны определения времен образования гаплогрупп R1a и R1b по снипам?

Пока совершенно ненадежны. Рассмотрим простой пример – два 67-маркерных базовых гаплотипа R1a-Z280 и R1b-P312. Их общий предок – гаплогруппа R1. Гаплогруппа R1a образовалась из гаплогруппы R1 примерно 20 тысяч лет назад[91], гаплогруппа R1b – примерно тогда же. Мои ранние датировки определяли возраст общих предков гаплогруппы R1a 20 тысяч лет назади, гаплогруппы R1b – 16 тысяч лет назад[92], недавние датировки времени образования гаплогруппы R1a по снипам дают для нее 105 снипов (компания YFull), то есть при 144 годах на снип получается возраст R1a, равный 15120 лет, хотя YFull заключили, что там должно быть 22100 лет; для R1b найдено всего 45 снипов, но YFull решили, что там тоже 22100 лет до общего предка (http:// www.yfull.com/tree/R1a/).

Таким образом компания YFull просто приравняла возраст R1b к R1a, без малейших обоснований, хотя снип-мутации происходят друг от друга совершенно независимо. У носителя гаплогруппы R1 примерно 20 тысяч лет назад проскочила снип-мутация в Y-хромосоме в нуклеотиде под номером 23 миллиона 473 тысячи 201, где был тимин, и он преобразовался в аденин.

Это сейчас назвали «снип М420». Но перед этим или после этого у других носителей гаплогруппы R1 проскочили еще три снип-мутации, разделенные, возможно, тысячелетиями – это превращение аденина в гуанин в участке Y-хромосомы под номером 17 миллионов 891 тысяча 241 (снип L62), превращение тимина в цитозин на участке под номером 18 миллионов 162 тысячи 834 (снип L63) и превращение цитозина в аденин на участке под номером 14 миллионов 138 тысяч 745 (снип L145). Сейчас у всех тестированных, имеющих гаплогруппу R1a, наблюдаются все четыре снипа – M420, L62, L63, и L145, и какой образовался раньше, какой позже, и сколько тысячелетий между ними – мы не знаем. Так какой возраст гаплогруппы R1a? И до какого снипа 105 мутаций? Мы опять же не знаем. Можно излагать «концептуально», не вдаваясь в детали, и ничего зазорного в этом нет. Но тогда не надо делать вид, что мы знаем детали, это – неправда. И YFull пишут – «22100 лет назад», прямо с точностью до 100 лет. А там – плюс-минус тысячелетия. Еще надо учесть, что здесь мы говорим не просто о носителях гаплогруппы R1 и их потомках R1a, а о тех, потомки которых выжили до настоящего времени.

Так вот, какое-то время назад у еще одного носителя гаплогруппы Rl,который жил тоже неизвестно когда, проскочила снип-мутация в положении Y-хромосомы под номером 2 миллиона 887 тысяч 824, которая превратила цитозин в аденин. Ее назвали снип М343, и он никакого отношения к указанным выше четырем снипам R1^R1a не имел. Вероятность того, что эти мутации произошли все или попарно в одно и то же время, практически нулевая. Зачем приравнивать их времена и писать – совершенно произвольно – что R1b образовался тоже 22100 лет назад, опять с точностью до ста лет, смысла никакого нет, разве что «по понятиям, для простоты».

В общем (и конкретно), мы не знаем. Но мы можем сравнить базовые гаплотипы субкладов R1a и R1b, время образования которых нам примерно известно, и определить, когда жил их общий предок, носитель гаплогруппы R1. А именно, из независимых данных, не по снипам. Об этом – ответ на следующий вопрос.

Вопрос 79: Что такое «медленная» 22-маркерная панель гаплотипов?

Эта панель была разработана для нахождения датировок особенно древних общих предков популяций. «Особенно древние» – это те, для которых возвратных мутаций в обычных маркерах гаплотипов настолько много, что мутации в маркерах приближаются к насыщению, и на время уже не реагируют. Точнее, число мутаций продолжает расти в «медленных» маркерах, но уже практически не растет в «быстрых» и прочих маркерах, и время до общего предка серии гаплотипов прогрессивно занижается.

Поэтому логика создания «медленной» панели гаплотипов была в том, чтобы изъять из гаплотипов «быстрые» маркеры, и оставить только медленные.

Приведем пример. Записываем базовые 67-маркерные гаплотипы субкладов R1a-Z280 и R1b-P312, упомянутых в ответе на предыдущий вопрос:

13 25 16 11 11 14 12 12 10 13 11 30–15 9 10 11 11 24 14 20 32 12 15

15 16–11 11 19 23 16 16 18 19 35 38 14 11–11 8 17 17 8 12 10 8 11

10 12 22 22 15 10 12 12 13 8 14 23 21 12 12 11 13 11 11 12 13

13 24 14 11 11 14 12 12 12 13 13 29 – 17 9 10 11 11 25 15 19 29 15

15 17 17 – 11 11 19 23 15 15 18 17 36 38 12 12 – 11 9 15 16 8 10

10 8 10 10 12 23 23 16 10 12 12 15 8 12 22 20 13 12 11 13 11 11

12 12

Между ними – 44 мутаций, что транслируется в 44/0.12 = 367 ? 568 условных поколений, или примерно 14200 лет. К этому нужно добавить «возраст» субкладов Z280 (4900 лет) и P312 (4300 лет), и разделить пополам. Это при формальном подходе означает, что их общий предок жил примерно 11700 лет назад. Этого, конечно, быть не может, так как гаплогруппы R1a и R1b имеют общего предка как минимум 20 тысяч лет назад. Ясно, что возраст общего предка субкладов, рассчитанный по 67-маркерным гаплотипам, значительно занижен.

Проверим по калькулятору Килина-Клёсова: результат – общий предок указанных субкладов жил 1367±2275 лет назад, при округлении получаем 13700±2300 лет назад. Все равно значительное занижение возраста общего предка, и мы уже знаем, почему – происходит насыщение аллелей из-за большого количества возвратных мутаций.

Переходим к «медленной» 22-маркерной панели. В нее входят следующие маркеры, с соответствующими константами скоростей мутаций, на условное поколение в 25 лет:

DYS426 0.00009

DYS388 0.00022

DYS392 0.00040

DYS455 0.00010

DYS454 0.00030

DYS438 0.00035

DYS531 0.00090

DYS578 0.00043

DYF395S1a 0.00040

DYF395S1b 0.00040

DYS590 0.00034

DYS641 0.00017

DYS472 0.000008

DYS425 0.000042

DYS594 0.00017

DYS436 0.00004

DYS490 0.00007

DYS450 0.00011

DYS617 0.00050

DYS568 0.00005

DYS640 0.00015

DYS492 0.00015

Суммарная скорость мутации – 0.00539 мутаций на гаплотип на условное поколение (25 лет).

В 22-маркерной панели базовые гаплотипы субклада R1a-Z280 и R1b-P312 имеют вид:

12 12 11 11 11 11 11 8 17 17 8 10 8 12 10 12 12 8 12 11 11 12

(R1a-Z280)

12 12 13 11 11 12 11 9 15 16 8 10 8 12 10 12 12 8 12 11 11 12

(R1b-P312)

Между ними – 7 мутаций, расстояние между гаплотипами транслируется в 7/0.00539 = 1299 условных поколений, которые следует откорректировать на влияние обратных мутаций (в 1.187 раз, получив 38548 лет), прибавить 4900 и 4300 лет и разделить пополам, получим 23874±9300 лет до общего предка. Видно, что это значительно более реалистично, чем 13700±2300 лет назад, хотя полученные величины перекрываются краями доверительных интервалов.

Проверим по калькулятору Килина-Клёсова: результат – общий предок указанных субкладов жил 26942±9642 лет назад, при округлении получаем 27000±0000 лет назад. Проверяем по данным YFull – датировка гаплогруппы R1 по снипам составляет 27600±2300 лет назад (http://www.yfull.com/tree/R1/). (Рис. 15) Взглянем на значительно более сложный случай – время жизни общего предка гаплогрупп R1a-Z280 (базовый гаплотип, 4900 лет до предка) и A0-V166 (современный гаплотип), датировка которого должна приближаться к 180 тысячам лет назад[93]:

12 12 11 11 11 11 11 8 17 17 8 10 8 12 10 12 12 8 12 11 11 12

(R1a-Z280)

12 13 10 10 11 10 11 8 15 15 8 9 8 0 10 9 14 8 12 8 11 12

(А0-V166)

Ручные расчеты здесь почти неприменимы, так как здесь число мутаций (18) приближается к числу маркеров в гаплотипах (22), и расчет с поправкой на возвратные мутации неустойчив. Калькулятор Килина-Клёсова показывает 187482^09316 лет, или округленно 190000±110000 лет до общего предка (Рис. 16).

Погрешности очень велики, потому что расчет ведется по двум относительно коротким гаплотипам.

Рис. 15. Расчет времени до общего предка гаплогрупп R1a-Z280 и R1b-P312 по их базовым гаплотипам в «медленном» 22-маркерном формате на калькуляторе Килина-Клёсова. Калькулятор показывает 26942±9642 лет до общего предка

Рис. 16. Расчет времени до общего предка гаплогрупп R1a-Z280 и А0-V166 по их базовым гаплотипам в «медленном» 22-маркерном формате на калькуляторе Килина-Клёсова. Калькулятор показывает 187482±109316 лет до общего предка

Рис. 17. Расчет времени до общего предка гаплогрупп А00 и A0-V166 по их базовым гаплотипам в «медленном» маркерном формате на калькуляторе Килина-Клёсова. Калькулятор показывает 217436±84643 лет до общего предка.

Рис. 18. Расчет времени до общего предка человека и шимпанзе по их базовым гаплотипам в «медленном» 22-маркерном формате на калькуляторе Килина-Клёсова. Калькулятор показывает 4 183 575 ± 1 508 531 лет до общего предка.

Следующий пример: время жизни общего предка гаплогруппы А00 (450 лет до общего предка популяции племени Mbo в Камеруне) и A0-V166 (современный гаплотип), датировка общего предка которых должна превышать 200 тысяч лет назад[94]. Здесь – 27 мутаций между двумя 22-маркерными гаплотипами, что делает расчеты вручную практически невозможными.

13 11 12 10 11 16 10 8 14 14 8 8 8 9 12 11 12 8 12 12 11 11

(А00)

12 13 10 10 11 10 11 8 15 15 8 9 8 0 10 9 14 8 12 8 11 12

(А0-V166)

Калькулятор Килина-Клёсова показывает 217436±84643 лет, или округленно 217000±85000 лет до общего предка. Это по современным представлениям датировка Homo sapiens как вида рода «люди» (рис. 17).

Наконец, рассмотрим самый сложный случай – датировка общего предка современного человека (базовый гаплотип экстраполирован к времени примерно 100 тысяч лет назад) и шимпанзе, по доступным маркерам (DYS426, 388, 392, 455, 438, 578, 641, 472, 425, 594, 436, 490, 617, 568, 640, 492)[95]

8 15 10 4 5 9 10 5 10 4 4 7 4 4 8 9

(шимпанзе)

11 12 11 11 10 8 10 8 12 10 12 12 12 11 11 11

(человек, 100000 лет назад)

Калькулятор показывает, что общий предок жил 4 183 575 ± 1 508 531 лет назад, или округленно 4.2 миллионов лет назад (рис. 18).

Но более надежный результат расчета получен без экстраполяции, путем расчета по гаплотипам шимпанзе и современного человека, и это показало, что их общий предок жил примерно 4.4 миллиона лет назад (рис. 26 ниже).

Вопрос 80: Какие типовые деревья гаплотипов наблюдаются в ДНК-генеалогии, каковы результаты их расчетов?

В ДНК-генеалогии встречаются симметричные, однородные деревья гаплотипов, которые с хорошей точностью описываются одним общим предком, от которого произошли большинство (или все) гаплотипов в данной выборке. Примером является большая выборка из 968 гаплотипов гаплогруппы I1

Рис. 19. Дерево из 968 гаплотипов гаплогруппы I1 в 111-маркерном формате

Все 968 гаплотипов имели 14891 мутаций в 67 маркерах, и 24990 мутаций в 111 маркерах. Это дает 14891/968/0.12 = 128 ? 147 условных поколений, или 3675±370 лет до общего предка по 67-маркерным гаплотипам, и 24990/968/0.198 = 130 ? 149 условных поколений, или 3725±370 лет до общего предка по 111-маркерным гаплотипам. Калькулятор Килина-Клёсова дает соответственно 3618±363 и 3686±369 лет до общего предка.

Еще пример – серия из 829 гаплотипов гаплогруппы R1b-U106 в 111-маркерном формате:

Рис. 20. Дерево из 829 гаплотипов гаплогруппы R1b-U106 в 111-маркерном формате

Все 829 гаплотипов имели 13254 мутаций в 67 маркерах, и 20874 мутаций в 111 маркерах. Это дает 13254/829/0.12 = 133 ? 154 условных поколений, или 3850±390 лет до общего предка по 67-маркерным гаплотипам, и 20874/829/0.198 = 127 ? 146 условных поколений, или 3650±370 лет до общего предка по 111-маркерным гаплотипам. Калькулятор Килина-Клёсова дает соответственно 3822±385 и 3850±387 лет до общего предка.

Значительно чаще встречаются деревья несимметричные, или еще более выраженные, с характерными ветвями. Так, 245 111-маркерных гаплотипов гаплогруппы I2 образуют следующее дерево:

Рис. 21. Дерево из 245 гаплотипов гаплогруппы I2 в 111-маркерном формате

В этом дереве можно выделить три основные ветви – верхнюю из 157 гаплотипов, и две нижних из 35 и 52 гаплотипов. Для краткости, приведем их датировки без подробных расчетов, и без округления. Для первой ветви, общий предок жил (расчет по 67-и 111-маркерным гаплотипам) 6986±707 и 7285±734 лет назад; для второй ветви – 3517±384 и 3542±374 лет назад; для третьей ветви 5098±533 и 5066±521 лет назад. Отметим, насколько согласуются данные для 67– и 111-маркерных гаплотипов.

Еще пример дерева гаплотипов с выраженной ветвью – для серии из 739 111-маркерных гаплотипов гаплогруппы J1.

Рис. 22. Дерево из 739 гаплотипов гаплогруппы J1 в 111-маркерном формате

Здесь нижняя ветвь (слева) состоит из 72 гаплотипов, ее общий предок жил (расчет по 67– и 111-маркерным гаплотипам) 8114±830 и 8469±859 лет назад; общий предок гаплотипов верхней ветви – 3355±337 и 3245±326 лет назад. Датировки здесь не округлены, и, строго говоря, представление данных в таком виде математически некорректно, здесь это представлено сугубо для иллюстрации. Некорректно – потому, что при погрешности в сотни лет давать датировки с точностью до одного года просто бессмысленно. Здесь еще одно упрощение – левая ветвь на дереве старше, чем правая, а общий расчет их «возраст» усреднил. То, что правая ветвь заметно «моложе» – видно и на глаз, там высота «гребенки» гаплотипов меньше. Левую ветвь мы будем анализировать ниже, при ответе на Вопрос 98, это – гаплотипы евреев и арабов, происходящие от одного общего предка, который жил примерно 4000 лет назад.

Экстремальные случаи неоднородных деревьев гаплотипов иллюстрируются, например, на рис. 13. Теоретически, расчет времени до общего предка для таких деревьев можно вести только в том случае, когда все ветви дерева имеют одинаковый «вес», то есть все ветви одинаковы по численности и по возрасту. На дереве на рис. 13 этого нет, и при расчетах по всему дереву, «чохом», получается «датировка» некого фантомного предка, не имеющая ничего общего с реальностью. Но так работают популяционные генетики. На самом деле нужно обработку каждой ветви проводить раздельно.

Вопрос 81. Почему константы скоростей мутаций – «константы», если они во всех маркерах разные?

Константами называют коэффициенты в уравнениях химической и биологической кинетики (кинетика – это наука о скоростях и механизмах химических и биологических реакций), которые показывают, как быстро или медленно реакция протекает. Простейшим уравнением кинетики является уравнение кинетики первого порядка, которое можно записать в виде с = с_о e^-kt, где с_о – это начальная концентрация вещества, которое претерпевает химические превращение, с – текущая концентрация, t – время, прошедшее с начала реакции, и k – константа скорости реакции. Это определение можно варьировать, в зависимости от рассматриваемой системы – например, в процессе радиоактивного распада мы уже не будем использовать слова «химическое превращение» и «химическая реакция», как и «текущая концентрация», хотя по сути можно использовать и их. Так вот, «константа» здесь не потому, что для разных реакций величина k будет одинакова, а потому, что в ходе реакции она остается постоянной. В процессах радиоактивного распада она «константа» еще и потому, что не зависит от размера образца радиоактивного материала. В серии гаплотипов она «константа» и потому, что не зависит от числа гаплотипов в серии, десятки там гаплотипов, сотни или многие тысячи.

Адаптируя это уравнение и определения к мутациям в гаплотипах, мы в качестве с_о рассматриваем базовые гаплотипы, в качестве с – количество оставшихся базовых гаплотипов в выборке, в качестве k – константу скорости мутации для данного маркера или гаплотипа. Эта константа остается постоянной – потому она и константа – в ходе убывания доли базовых гаплотипов в системе.

Пример. Имеем выборку, например, из сотни гаплотипов прямых потомков общего предка. Пусть гаплотипы будут в 67-маркерном формате. Понятно, что сто потомков одного предка появятся не сразу, на их появление требуется время. Допустим, прошло 500 лет, то есть 20 условных поколений. Те ДНК-линии, в которых рождались девочки, или детей вообще не было, не попадают в выборки будущего. Если в поколении рождалось по одному мальчику, то через 20 поколений вся максимально возможная выборка будет состоять только из одного человека, потомка того предка 500 лет назад. Если в каждом поколении рождалось по два мальчика, то через 10 поколений потомков будет уже 1024 человек, а через 20 поколений – чуть больше миллиона человек, конечно, в идеальном случае. Понятно, что это упрощения, но ясно, что через 10 поколений, то есть примерно 250 лет, выборку в сотню потомков уже можно набрать.

Покажем, как константа скорости мутации, будучи именно константой, описывает убывание базовых гаплотипов в системе. Через 10 поколений в ста гаплотипах потомков предковые (базовые) 67-маркерные гаплотипы останутся только у 30 человек. Проверим: [ln(100/30)]/0.12 = 10 (условных поколений). Через 13 поколений базовые гаплотипы останутся у 20 человек. Через 19 поколений – у 10 человек. Через 25 поколений – у пяти человек. Через 32 условных поколения, то есть через 800 лет, базовые гаплотипы останутся только у двух человек: [ln(100/2)]/0.12 = 32 (условных поколения).

Как мы видим, константа скорости мутации (для 67-маркерных гаплотипов равная 0.12 мутаций на гаплотип на поколение) остается неизменной, и определяет, с какой скоростью убывают базовые гаплотипы в потомках. Естественно, при переходе к более коротким гаплотипам, например, 12-маркерным, базовые гаплотипы сохраняются у многих потомков тысячелетиями. Например, два базовых 12-маркерных гаплотипа из ста сохранятся через [ln(100/2)]/0.02 = 196 условных поколений, то есть почти через пять тысяч лет.

Эти же закономерности соблюдаются для всех индивидуальных маркеров во всех гаплотипах, как было показано при реальных исследованиях[96].

Вопрос 82: Могут ли на величины констант скоростей мутаций в гаплотипах влиять факторы окружающей среды?

Это маловероятно, и скорее всего не могут. Во всяком случае, константы скоростей мутаций в гаплотипах одни и те же во всех регионах мира, и во всех изученных гаплогруппах. Никаких данных, которых бы этому противоречили, нет. В литературе (обычно сетевой) не раз объявлялось, что скорости мутаций разные в разных гаплогруппах, причем это объявлялось на единичных примерах, но каждый раз оказывалось, что расчеты проводились неквалифицированно и просто некорректно. В зарубежной литературе иногда цитируют данные Kirchner, который якобы показал разницу в скоростях мутаций для нескольких гаплогрупп, но во всех случаях расчеты проводились опять на единичных примерах, порой на двух-трех гаплотипах. Никакого подобия статистической обработки данных не было.