Книга: Естествознание. Базовый уровень. 10 класс

Модель «хищник – жертва»

Рассмотрим широко известную в экологии модель, описывающую изменение численности двух видов, обитающих на данной территории: жертвы и хищника. Допустим, в определённой местности живут зайцы и лисы. Будем считать, что пища для зайцев имеется в избытке и поэтому они могут быстро размножаться в геометрической прогрессии. Следовательно, чем больше зайцев живёт в этом году, тем больше их родится в следующем. Так бы они и размножались бесконечно, если бы поблизости не обитали лисицы.

Эти хищники питаются зайцами и значительно сокращают их численность. Поэтому мы можем записать: зайцы + лисы ? меньше зайцев.

Однако если зайцев окажется слишком мало, лисам станет нечего есть и они начнут вымирать от голода. Поэтому мы можем также написать другое уравнение: лисы – зайцы ? меньше лис.

Попробуем решить систему этих уравнений, не прибегая к математическим вычислениям. Это будет называться качественным решением. Предположим, что в начальный момент у нас имеется некоторое число лис и достаточное число зайцев, чтобы лисы не ограничивали себя в питании. В этих условиях хищники начнут быстро размножаться и, когда их станет достаточно много, они станут съедать столько зайцев, что численность жертв начнёт убывать. Но по мере того как зайцев будет становиться всё меньше, лисам станет не хватать еды и они начнут вымирать от недостатка питания. Когда же их станет совсем мало, зайцы, оказавшиеся в относительной безопасности, снова начнут усиленно размножаться. Затем этот цикл повторится, и мы получим график, изображённый на рисунке (рис. 29). Он представляет собой две сдвинутые относительно друг друга колебательные линии, похожие на синусоиды.

Такая модель позволяет в известных пределах прогнозировать изменение численности обитающих на данной территории животных. Конечно, она, как любая модель, не свободна от упрощения и идеализации. Может, например, выдаться засушливое лето, и тогда наше предположение, что пища у зайцев всегда имеется в избытке, окажется неверным. В лес могут приехать охотники и сократить численность лис гораздо значительнее, чем это предполагает модель. В таком случае, если модель даёт неточные результаты, её, как было сказано, дорабатывают: вводят дополнительные факторы или исправляют алгоритмы. Любая модель, особенно в таких системах, где присутствует много случайных факторов, всегда должна быть динамичной и развивающейся.

Заканчивая разговор о математических моделях, обратим внимание ещё на одно интересное обстоятельство. Часто математические модели, разработанные для одного класса явлений, оказываются применимыми в совершенно другой области.

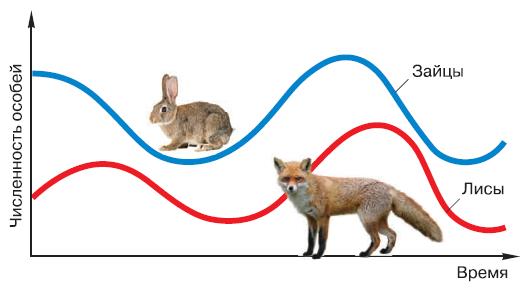
Рис. 29. Колебания численности популяций лисиц и зайцев

Те же математические уравнения, с помощью которых описывается взаимоотношение «хищник – жертва», с успехом используются при расчёте некоторых химических реакций. Это говорит об общности законов природы и присутствии в ней единых закономерностей.