Книга: Как работает Вселенная: Введение в современную космологию

5.1. Космологические свидетельства существования темной материи и темной энергии

Перейдем от масштабов галактик, т. е. астрономических, к масштабам космологическим. Это позволяет решить несколько задач. Во-первых, получить независимые оценки ?m – плотности материи, выраженной в процентах от критической плотности. Во-вторых, разделить вклады темной и барионной материй. Для этого вводится аналогичный параметр ?b – отношение плотности барионной материи к критической. Понятно, что плотность небарионной темной материи в процентах от критической плотности будет равна ?m – ?b. В-третьих, кроме этого, естественно получаются оценки параметра ?? – отношения плотности энергии, связанной с космологической постоянной, к критической плотности энергии. В настоящее время космологическая постоянная рассматривается как один из частных случаев темной энергии, о которой мы расскажем ниже.

Еще до открытия реликтового излучения космологи мечтали о двух типах космических объектов, которые позволили бы им разобраться с геометрией пространства-времени, в частности определить знак кривизны Вселенной. Первый тип объектов получил жаргонное название «стандартная свеча». Это объекты, которые обладают одинаковой светимостью, но при этом находятся на очень разных расстояниях от Земли. Второй тип объектов называется стандартной линейкой и имеет одинаковые линейные размеры. Зачем эти объекты были так нужны? Дело в том, что в искривленном пространстве, как мы уже упоминали в разделе 2.5, понятие расстояния становится неоднозначным. Вводятся несколько видов расстояний, которые связаны друг с другом через кривизну пространства.

Имея стандартную свечу, мы можем ввести так называемое фотометрическое расстояние. По определению, это расстояние, на которое нужно в плоском пространстве отнести источник света, чтобы получить наблюдаемый поток света. Его отличие от обычного расстояния связано с двумя факторами. Первый из них связан с тем, что освещенность поверхности обратно пропорциональна квадрату расстояния до точечного источника света. Это справедливо только для плоского пространства. В пространстве с положительной кривизной поверхность сферы радиуса r меньше чем 4?r2. Соответственно, освещенность будет падать медленнее, чем r–2. Понятно, что в пространстве с положительной кривизной, где поток больше, чем в плоском пространстве, благодаря только первому фактору, фотометрическое расстояние будет меньше, чем в плоском. Соответственно, в пространстве отрицательной кривизны, где площадь поверхности сферы больше чем 4?r2, фотометрическое расстояние было бы больше, чем в плоском пространстве при одинаковых потоках.

Второй фактор связан с тем, что свет от удаленных источников был излучен в более ранней Вселенной и за время распространения длина его волны увеличилась в 1 + z раз. Соответственно, энергия фотонов, пропорциональная частоте, уменьшилась в 1 + z раз. Кроме того, в 1 + z раз увеличилось время между приходами фотонов. В результате в формуле для потока света, наблюдаемого на Земле, возникает множитель (1 + z)–2, что увеличивает фотометрическое расстояние в 1 + z раз.

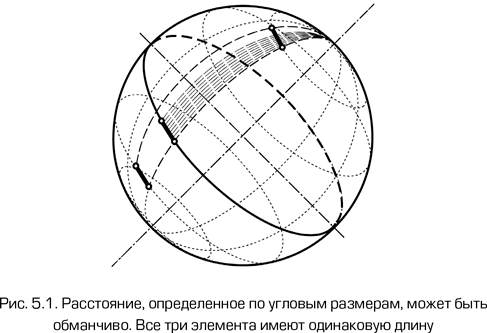
Имея стандартную линейку, мы можем ввести понятие расстояния, определенного по угловым размерам. В плоском пространстве объект длиной l на расстоянии r >> l виден под углом ? = l/r в радианной мере. Соответственно, расстояние может быть определено по формуле r = l/?. В кривом пространстве все куда сложнее. Рассмотрим поверхность сферы, например Земли (см. рис. 5.1). Пусть наблюдатель находится на Северном полюсе и измеряет угловые размеры метровой линейки, расположенной точно вдоль параллели. Поскольку в двумерном пространстве с положительной кривизной свет распространяется по большому кругу, фактически нам необходимо вычислить разность долгот западного и восточного концов линейки. По мере удаления линейки от наблюдателя ее угловые размеры будут уменьшаться, достигнут минимума на экваторе, а затем снова начнут увеличиваться при приближении к Южному полюсу[77]. При этом угловой размер линейки на экваторе будет равен 2??1 м/40 000 км. В плоском же пространстве угловой размер линейки будет равен 1 м/10 000 км. Таким образом, в пространстве с положительной кривизной минимальный угловой размер линейки будет в ?/2 ? 1,57 раз больше, чем в плоском, независимо от величины кривизны. Соответственно, расстояние по угловым размерам будет меньше, чем в плоском пространстве. В пространстве с отрицательной кривизной ситуация будет обратной: расстояние по угловым размерам будет больше, чем в плоском пространстве.

Кроме этого, у нас существует уже введенное расстояние по красному смещению, которое легко определяется для любого астрономического объекта по его спектру. Имея стандартную свечу, мы можем построить график зависимости фотометрического расстояния от расстояния по красному смещению, который даст нам необходимую информацию о свойствах пространства. Аналогично, имея стандартную линейку, мы можем построить зависимость расстояния по угловым размерам от расстояния по красному смещению. Как видим, достаточно иметь либо свечу, либо линейку. Если же имеется и то и другое, мы можем получить две независимые оценки кривизны Вселенной.

Раньше в качестве стандартных свечи и линейки пытались использовать галактики, предполагая, что их светимость и линейные размеры постоянны. Эти попытки не увенчались успехом, что не удивительно, учитывая, что галактики довольно сильно отличаются друг от друга. В настоящее время мы имеем куда более совершенных кандидатов на роль стандартной свечи и стандартной линейки.