Книга: Как работает Вселенная: Введение в современную космологию

4.2.2. Кривые вращения галактик

4.2.2. Кривые вращения галактик

Как астрономы определили массы других галактик? Наиболее простой способ заключается в построении кривой вращения данной галактики. Это скорость, с которой звезды вращаются вокруг центра галактики в зависимости от расстояния до этого центра. Пусть звезда вращается по круговой орбите радиуса r. Обозначим M(r) массу части галактики, заключенной внутри сферы радиуса r. Если эта масса сосредоточена в центре или распределена сферически симметрично, то скорость вращения звезды v(r) определим из условия равенства силы притяжения к центру и центробежной силы. Естественно, мы получим формулу Кеплера для движения по круговой орбите

Осталась одна небольшая деталь: научиться измерять зависимость v(r). Не для всех галактик это возможно. Если плоскость галактики перпендикулярна направлению на Землю, то скорости вращения звезд имеют только тангенциальные компоненты и не могут быть измерены существующими методами. Если же плоскость галактики наклонена, то скорости вращения звезд имеют еще и радиальные компоненты. В этом случае их можно определить по эффекту Доплера. На рис. 4.2 показана галактика, вращающаяся против часовой стрелки так, что спиральный рукав в точке A движется на нас, а в точке C – от нас. Рисунок сделан в галактической плоскости, наблюдатель на Земле расположен внизу. Эти скорости вращения складываются со скоростью, с которой центр галактики, расположенный в точке B, удаляется от нас. В результате в точке A спектры излучения будут дополнительно сдвинуты в фиолетовую область по сравнению с точкой B, а в точке C – в красную область. Анализируя наблюдаемый спектр галактики, можно определить направление вращения галактики и скорость вращения ее частей. Далее, зная угол наклона плоскости галактики к направлению на Землю, мы можем определить форму кривой вращения. Угол наклона определяется из предположения, что диск галактики круглый, а наблюдаемая эллиптичность связана с ее наклоном. Чем больше угол наклона, тем точнее можно определить кривую вращения. В этом смысле идеальными являются галактики, видимые с ребра.

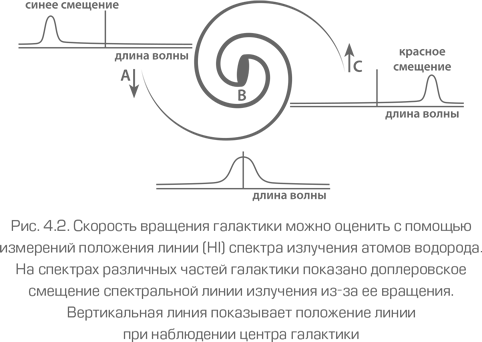
Естественно, что для того, чтобы получить кривую вращения, мы должны рассмотреть с помощью телескопа разные части галактики. Это можно сделать только для не очень далеких галактик. Для галактик со слишком маленькими угловыми размерами мы не можем получить кривую вращения. Вместо этого мы можем определить ширину линий излучений галактики. В основном она связана с доплеровским сдвигом света, излученного разными частями галактики. В результате вместо кривой вращения мы можем получить только оценку характерной средней величины скорости вращения. Ширина линий излучения активно используется во внегалактической астрономии, но для иллюстрации существования темной материи кривые вращения куда нагляднее.

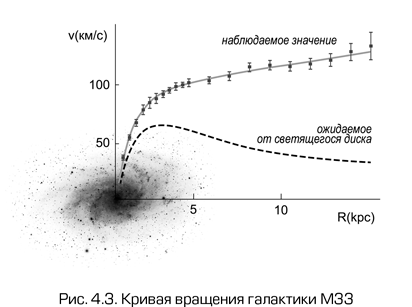
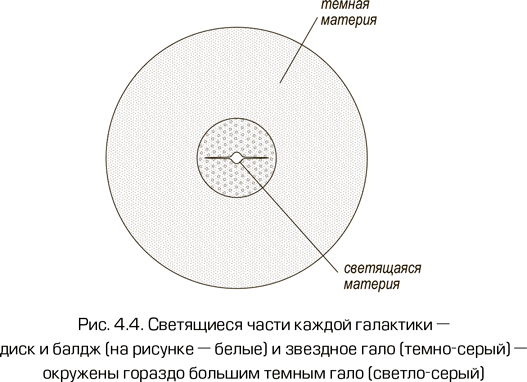
На рис. 4.3 показано изображение галактики M33 (Треугольник), входящей в Местную группу, т. е. одной из самых близких к нам галактик. На него наложена кривая вращения этой галактики таким образом, что масштаб расстояний совпадает с масштабом изображения. Обратим внимание, что кривая вращения приведена для области, существенно превосходящей видимые размеры галактики. Как это было сделано? Для этого использовались наблюдения небольших водородных облаков, вращающихся вокруг галактики вне ее видимой области. Естественно, закон Кеплера для них выполняется точно так же, как и для звезд. На рисунке кроме реальной кривой вращения изображена теоретическая кривая вращения, которую имела бы эта галактика, если бы вся ее масса была сосредоточена в светящейся компоненте. Легко понять, что за пределами видимой части галактики M(r) доля светящейся материи становится постоянной и v(r) в отсутствие темной материи падала бы по закону v ~ r–1/2. В то же время реальная кривая вращения, напротив, продолжает возрастать далеко за пределами видимой области, показывая, что там должно существовать нечто, вносящее вклад в общую массу галактики. Это и есть темная материя. Согласно существующим представлениям, все галактики окружены гало из темной материи (см. рис. 4.4), размеры которого существенно превосходят размеры видимой части галактики.

Если мы посмотрим на кривые вращения чуть более далеких галактик, то увидим, что v(r) иногда выходит на постоянное значение в широких интервалах изменения r. Такие кривые вращения называются плоскими. Забавно, что в Facebook даже была создана специальная группа сторонников того, что все кривые вращения можно считать плоскими. Эта группа с незатейливым названием «Кривые вращения галактик – плоские» выпустила по этому поводу свой меморандум. Вскоре после этого в той же соцсети появилась группа противников подобного обобщения, справедливо указывающая, что далеко не все кривые вращения галактик можно считать плоскими. Она также выпустила свой меморандум, а ее лидеры организовали серию научных семинаров по всему миру с целью развеять этот миф. К счастью, в научном мире справедливость той или иной гипотезы не определяется количеством лайков в социальных сетях.

Существует одна галактика, кривую вращения которой нельзя определить описанным выше способом. Это – наша Галактика, которую мы видим изнутри. Тем не менее кривая вращения нашей Галактики также получена астрономами, правда с меньшей точностью, чем для близлежащих галактик. Из параметров орбиты Солнца вокруг центра Галактики (радиус – 26 400 св. лет, период – 230 млн лет) по закону Кеплера нетрудно рассчитать массу материи, заключенную внутри орбиты Солнца, – она равняется 1,0?1011 M?. Полная же масса нашей Галактики составляет около 1012 M?.