Книга: Эволюция разума

Разреженное кодирование: векторное квантование

Разреженное кодирование: векторное квантование

В начале 1980-х гг. я начал заниматься проектом, посвященным другой классической проблеме распознавания образов — пониманию человеческой речи. Сначала мы использовали классический подход, заключающийся в прямом программировании знаний о фундаментальных единицах речи, называемых фонемами, и лингвистических правилах связывания отдельных фонем в слова и фразы. Каждая фонема характеризуется определенными частотными параметрами. Например, мы знаем, что такие гласные, как «и» и «а», характеризуются определенными резонансными частотами, называемыми формантами, причем каждой фонеме соответствует определенное соотношение формант. Свистящие звуки, как [з] и [с], характеризуются шумовым импульсом, охватывающим несколько частот.

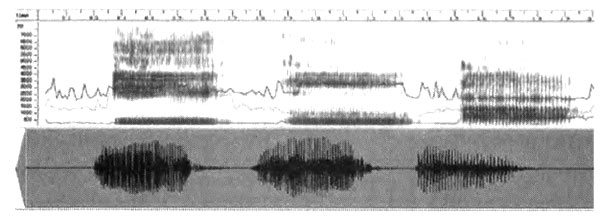
Спектр трех гласных звуков. Слева направо: звук [i], как в слове «appreciate», [и], как в «acoustic», и [а], как в «ah». По оси Y отложены звуковые частоты. Чем темнее полосы, тем больше энергии соответствует этой частоте.

Мы регистрировали речь в виде звуковых волн, которые затем конвертировали в частотные полосы, используя частотные фильтры. Результат такой трансформации (спректрограмма) выглядит следующим образом.

Фильтры имитируют функцию улитки человеческого уха на начальном этапе биологического процесса восприятия звука. Компьютерная программа сперва идентифицировала фонемы на основании распознанных частот, а затем на основании характерных последовательностей фонем идентифицировала слова.

Кое-что у нас получилось. Мы смогли натренировать нашу систему на распознавание речи конкретного человека, пользовавшегося небольшим набором слов (несколько тысяч). Далее мы попытались научить ее распознавать десятки тысяч слов, речь разных людей и непрерывную речь (без пауз между словами), но столкнулись с проблемой инвариантности. Разные люди произносят одну и ту же фонему по-разному: в устах одного человека фонема «и» может звучать, как «а» у другого человека. Даже один и тот же человек не отдает себе отчета в том, как он произносит отдельные фонемы. Характер звучания часто зависит от соседних фонем. Некоторые фонемы полностью исчезают. Произношение слов (то есть сочленение фонем) также весьма вариабельно и зависит от контекста. Те лингвистические правила, которые мы заложили в нашу программу, не смогли учесть чрезвычайную вариабельность разговорной речи.

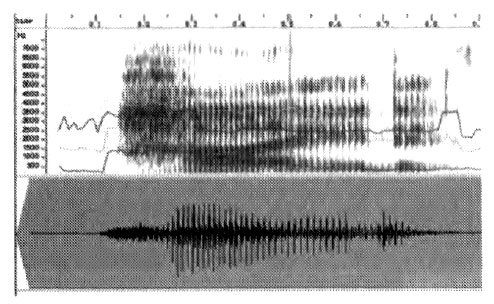
Спектр слова «hide» («хайд» — прятать). Горизонтальные линии соответствуют формантам — частотам с наиболее высокой энергией.

Тогда мне стало ясно, что распознавание образов и понятий человеческим мозгом имеет иерархическую природу. Это совершенно очевидно для человеческой речи, состоящей из сложных иерархических структур. Но что лежит в основе этой структуры? Это был первый вопрос, который я задал себе, собираясь заниматься созданием автоматических систем распознавания разговорной человеческой речи. Звук проникает в ухо как вибрация воздуха и под действием примерно 3000 внутренних волосковых клеток внутри ушной улитки превращается во множество полос различной частоты. Каждая волосковая клетка настроена на восприятие определенной частоты (звуковые частоты мы воспринимаем как тона), и каждая действует как частотный фильтр, испуская сигнал, когда улавливает звук своей или близкой резонансной частоты. Таким образом, выходящий из улитки уха звук составлен примерно из 3000 отдельных сигналов, каждый из которых характеризуется изменяющейся во времени интенсивностью узкой звуковой полосы (конечно, эти полосы перекрываются).

Даже при условии множественных повторов структур мозга мне кажется совершенно невероятным, что мозг обрабатывает 3000 отдельных звуковых сигналов. У меня вызывала большое сомнение столь низкая эффективность эволюции. Теперь мы знаем, что еще до того, как звуковые сигналы попадают в новую кору, в слуховом нерве происходит очень значительное сокращение объема информации. В наших искусственных системах распознавания речи мы тоже применяли фильтры (сначала 16, а потом 32; больше, как оказалось, использовать бессмысленно). Таким образом, в нашей системе в каждый момент времени входной сигнал был представлен 16 числами. И нам предстояло свести эти 16 потоков данных к единому потоку, сохранив при этом информацию, необходимую для распознавания речи.

С этой целью мы использовали математический метод, называемый векторным квантованием. Итак, представьте себе, что в любой момент времени звук (выходящий из уха к мозгу) представлялся компьютерной программой в виде набора из 16 чисел — выходные сигналы, прошедшие 16 частотных фильтров (в человеческом ухе было бы 3000 чисел, соответствующих выходным сигналам из 3000 волосковых клеток). На языке математики каждый подобный набор чисел (3000 в биологической системе или 16 в компьютерной модели) называют вектором.

Для простоты рассмотрим процесс векторного квантования для вектора из двух чисел. Каждый вектор можно представить себе в виде точки в двумерном пространстве.

Если у нас имеется множество таких векторов, при нанесении их на график мы можем заметить формирование определенных кластеров.

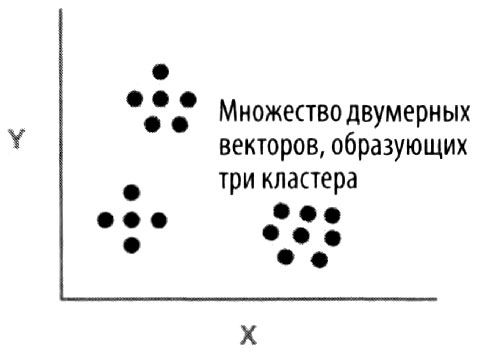
Для идентификации кластеров нужно решить, сколько их будет. В нашей работе мы обычно допускали существование 1024 кластеров, которые могли пронумеровать и обозначить 10-разрядным двоичным числом (поскольку 2¹⁰ = 1024). Наша выборка векторов представляет необходимое нам разнообразие. Сначала мы предполагали, что первые 1024 вектора образуют одноточечные кластеры. Затем мы рассматривали 1025-й вектор и находили ближайшую к нему точку. Если это расстояние больше самого маленького расстояния между двумя любыми точками из 1024, мы считаем эту точку началом нового кластера. Тогда мы «схлопываем» два ближайших кластера в единый кластер (при этом у нас по-прежнему остается 1024 кластера).

После добавления 1025-го вектора один из наших кластеров содержит более одной точки. Мы продолжаем действовать таким же образом, все время сохраняя 1024 кластера. Когда мы добавим все точки, мы можем представить каждый многоточечный кластер в виде геометрического центра точек этого кластера.

Кластер точек; мы можем его изобразить в виде единственной точки, соответствующей геометрическому центру всей этой группы точек.

Мы повторяем этот процесс до тех пор, пока не учтем все точки из нашей выборки. Обычно мы укладываем в 1024 (2¹⁰) кластера миллионы точек (мы также работали с 2048 (2¹¹) и с 4096 (2¹²) кластерами). Каждый кластер можно представить в виде единственного вектора, расположенного в геометрическом центре всех точек кластера. Таким образом, сумма расстояний от всех точек кластера до центральной точки минимальна.

В результате применения данного метода вместо миллионов точек, с которыми мы начинали работать, у нас остается всего 1024 точки, оптимальным образом распределенные в пространстве. Неиспользованные части пространства не принадлежат ни одному кластеру.

Далее мы нумеруем наши кластеры (в данном случае приписываем им номера от 0 до 1023). Этот номер является сокращенным, «квантованным» представлением кластера, вот почему данный метод называется методом векторного квантования. Любой новый входящий вектор будет характеризоваться номером кластера, центр которого расположен ближе всего к этому новому вектору.

Теперь мы можем рассчитать расстояние от центра каждого кластера до центра всех других кластеров. Тем самым мы получаем расстояние от этого нового входящего вектора (представленного квантованным значением — номером кластера, к которому новый вектор расположен ближе всего) до всех других кластеров. Поскольку все точки характеризуются только номерами ближайших кластеров, мы знаем расстояния между конкретной точкой и всеми другими возможными точками.

Я описал суть метода в применении к двумерным векторам, но работа с 16-мерными векторами осуществляется по совершенно аналогичной схеме. Мы выбираем векторы с 16 числами, соответствующими 16 различным частотным полосам, так что каждая точка в нашей системе располагается в 16-мерном пространстве. Нам трудно вообразить пространство, распространяющееся более чем в трех измерениях (ну максимум в четырех, если мы добавим шкалу времени), но у математиков нет таких ограничений.

Применение данного метода позволило нам решить четыре задачи. Во-первых, мы значительно понизили уровень сложности системы. Во-вторых, мы представили 16-мерные данные в виде одномерных. В-третьих, мы усовершенствовали свою способность находить инвариантные черты, поскольку выделяем те участки звукового пространства, которые содержат наибольшее количество информации. Большинство комбинаций частот является физически невозможным или очень маловероятным, поэтому нет смысла выделять одинаковое пространство для вероятных и маловероятных комбинаций входных сигналов. Этот метод позволяет ограничить набор данных равновероятными возможностями. Четвертое достижение заключается в том, что мы можем использовать одномерные распознающие модули, даже если исходные данные являются многомерными. Это самый эффективный подход к использованию имеющихся в настоящее время вычислительных ресурсов.