Книга: Астероидно-кометная опасность: вчера, сегодня, завтра

9.4. Палермская техническая шкала для оценки угрозы столкновения Земли с астероидами и кометами

9.4. Палермская техническая шкала для оценки угрозы столкновения Земли с астероидами и кометами

Туринская шкала, рассмотренная в предыдущем разделе, была разработана прежде всего для описания и распространения сведений об астероиднокометной опасности средствами массовой информации. Она проста и доступна для понимания неспециалистов. Но те упрощения, которые были сознательно допущены при ее разработке, делают шкалу малопригодной для использования в научных исследованиях. Отметим несколько таких упрощений.

Важной особенностью Туринской шкалы является то, что она целочисленная. Это облегчает восприятие оценки. Но события, относящиеся к одной и той же категории по Туринской шкале, фактически могут весьма сильно отличаться друг от друга. Например, два события, имея одинаковую вероятность, могут на два-три порядка отличаться по энергии столкновения. С другой стороны, мало отличающиеся друг от друга события могут оказаться по разные стороны границы раздела между областями и, как следствие, иметь различные категории, при этом не всегда различающиеся на единицу. Более того, в окрестности узловых точек близкие события отвечают целому набору различных категорий шкалы.

Любое событие с энергией, меньшей 1 Мт, согласно Туринской шкале, имеет категорию 0. С точки зрения не привлечения общественного внимания к подобным событиям, это оправдано. Но в научном плане отслеживание событий с меньшими значениями энергии часто представляет интерес, и надо иметь возможность оценивать такие события по их важности для научного исследования. То же самое можно сказать и в отношении событий весьма маловероятных, но сопряженных с большой энергией столкновения.

Туринская шкала предназначена для оценки событий, происходящих в течение ближайшего столетия. Формально говоря, события более отдаленного будущего не имеют определенной категории по этой шкале. Между тем, уже сейчас для некоторых астероидов достаточно точные прогнозы столкновений могут быть сделаны на существенно более длительные интервалы времени. Более того, оценка по Туринской шкале не зависит непосредственным образом от времени до предстоящего сближения: вне зависимости от того, сколько времени осталось до сближения — несколько месяцев или несколько десятков лет — по Туринской шкале это событие получает одну и ту же оценку. Фактор времени влияет лишь опосредствованно, поскольку более близкое событие привлекает, естественно, больше внимания.

Таким образом, можно отметить, что для научных целей требуется система, которая позволяла бы оценивать различные события с точки зрения создаваемой ими угрозы вне зависимости от диапазона энергии, вероятности и времени до столкновения, причем эта система должна обеспечивать непрерывность и сглаженность оценки в любом диапазоне. Справедливости ради надо отметить, что идея создания такой шкалы была в общих чертах сформулирована в работе [Binzel, 2000], посвященной описанию Туринской шкалы. Но в развитом виде подобная шкала была представлена группой докладчиков на конференции в Палермо «Asteroids 2001. From Piazzi to the Third Millennium», посвященной двухсотлетию открытия первого астероида. Поэтому данная шкала получила название Палермской [Chesley et al., 2002].

В указанной работе авторы прежде всего вводят понятие «ожидаемой энергии» события ?, которая определяется как произведение вероятности события P_I на его энергию E:

В том случае, когда тело несколько раз сближается с Землей на рассматриваемом интервале времени, причем каждому сближению соответствует определенная вероятность столкновения, для каждого события может быть вычислена ожидаемая энергия, и для всей последовательности событий может быть вычислена «совокупная ожидаемая энергия» как сумма ожидаемых энергий частных событий.

Далее авторы сопоставляют энергию и вероятность ожидаемого столкновения с соответствующими фоновыми значениями, обусловленными случайными столкновениями Земли с астероидами и кометами за время, остающееся до рассматриваемого события. При этом учитывается осредненная на длительном интервале времени частота столкновений. Частота падения на Землю тел с энергией, большей или равной заданному значению E, может быть определена как

где энергия E исчисляется в мегатоннах.

Формула (9.12) выражает зависимость, очень близкую к эмпирическому распределению, найденному Е. Шумейкером главным образом на основании подсчета числа лунных кратеров [Shoemaker, 1983]. Заметим, что частоту падения тел на Землю при условии ее малости (именно с такими событиями приходится иметь дело) можно рассматривать как годичную вероятность событий.

На рис. 9.9 представлена частота столкновения Земли с космическими телами как функция энергии. Учитываются тела с энергией, большей или равной заданной величине E. Кривая линия — эмпирическое распределение, основанное преимущественно на результатах Шумейкера [Chapman and Morrison, 1994]. Прямая линия — аппроксимация, определяемая формулой (9.11). Для сравнения штриховой линией показана частота столкновений по Туринской шкале.

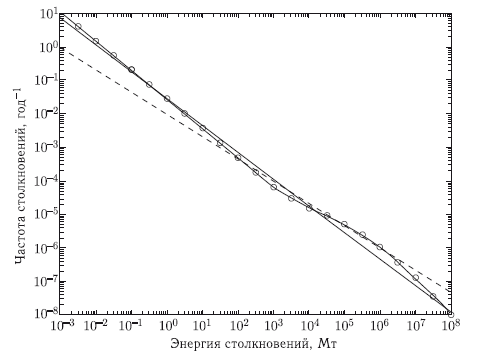
^{Рис. 9.9. Частота столкновения Земли с космическими телами как функция энергии [Chesley et al., 2002]}

Математически величина ?B представляет собой определенный интеграл:

где ?(E) — частота столкновения Земли с телами, обладающими энергией E. Дифференцируя интеграл (9.13) по нижнему пределу и используя формулу (9.12), находим выражение для этой частоты в виде

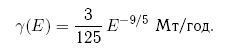
Найдем теперь ожидаемый поток энергии ?B(E, ?), приносимой на Землю в течение года падающими на нее телами в некотором диапазоне энергии от ?^-1E до ?E:

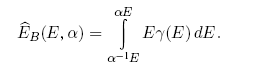
Теперь имеется возможность сравнить ожидаемую энергию столкновения ? для рассматриваемого события с общей энергией, приносимой на Землю телами в некотором диапазоне энергии от ?^-1E до ?E за время, оставшееся до столкновения. Последняя величина, очевидно, равна

где ?T — время до столкновения, выраженное в годах.

Искомое отношение R_?, равное

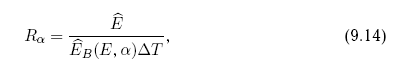
можно квалифицировать как ожидаемую энергию столкновения, взвешенную по отношению к потоку энергии, приносимой телами подобного же размера за оставшееся до столкновения время.

Можно показать, что, выбирая ? равным 1,865, выражение (9.14) можно свести к следующему:

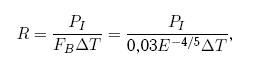
которое в Палермской шкале получило наименование «нормализованного риска». Другими словами, нормализованный риск — это вероятность столкновения тела с Землей, взвешенная по отношению к вероятности столкновения с Землей тел такой же или большей энергии за время, оставшееся до предполагаемого столкновения. Десятичный логарифм этой величины P определяет Палермскую техническую шкалу для оценки угрозы столкновения тел с Землей:

Все вышесказанное применимо равным образом и тогда, когда астероид или комета имеют на рассматриваемом интервале времени серию сближений с Землей. В этом случае вычисляется совокупный нормализованный риск, который сопоставляется с фоновым риском, исчисляемым за время до конца рассматриваемых событий.

Исходя из определения Палермской шкалы, можно отметить, что события, получающие оценку ноль, представляют такую же угрозу, которую создает естественный фон тел, способных сближаться с Землей, такой же или большей энергии. Значение шкалы –2 соответствует событию, представляющему в сто раз меньшую опасность по сравнению с естественным фоном, а оценка +3 означает событие в тысячу раз более опасное по сравнению с вероятными столкновениями Земли со случайными телами такой же энергии за время, остающееся до события.

Как связаны друг с другом Туринская и Палермская шкалы? Это разные шкалы. Не существует правила перехода от одной шкалы к другой, хотя бы уже потому, что Палермская шкала непрерывная, а Туринская — целочисленная. В целом, если событие имеет вероятность, большую чем фоновые события, то и по Палермской, и по Туринской шкале они имеют оценку, превосходящую 0. С другой стороны, события, имеющие оценку 1 по Туринской шкале, часто по Палермской шкале оказываются отрицательными, достигая по абсолютной величине нескольких единиц.

Наивысшую оценку по Туринской шкале, равную 4, имел в конце декабря 2004 г. астероид 2004 MN4, впоследствии получивший номер (99942) и имя Апофис (см. главу 7).

Еще один астероид (144898) 2004 V D₁₇ с февраля по май 2006 г. имел оценку 2 по Туринской шкале из-за возможного столкновения с Землей в 2102 г. После новых наблюдений астероида эта оценка в конце концов была понижена до нуля. В настоящее время оценку 1 по Туринской шкале имеет астероид 2007 V K₁₈₄. В 2048–2057 гг. он будет четырежды сближаться с Землей, причем суммарная оценка вероятности столкновения составляет 3,4 10^-4. Оценка угрозы по Палермской шкале равна –1,82.

Наибольшую оценку по Палермской шкале, которая может достигать величины +0,17, в настоящее время имеет астероид (29075) 1950 DA, который был открыт еще в 1950 г., но затем был утерян на целых пятьдесят лет до 31 декабря 2000 г. Объединение наблюдений 1950 г. с наблюдениями 2000–2001 гг. позволило существенным образом уточнить орбиту астероида. В период его очередного сближения с Землей 3–7 марта 2001 г. были выполнены радиолокационные наблюдения астероида, которые дали возможность определить его форму и размеры (слегка асимметричный сфероид со средним диаметром около 1,1 км), а также возможные положения в пространстве его оси вращения. Период вращения оказался одним из самых коротких для тел подобного размера — всего лишь 2,12 ч.

Когда орбита астероида была уточнена с учетом оптических и радарных наблюдений и был выполнен прогноз движения астероида в будущем, оказалось, что он будет иметь необычайно тесное сближение с Землей 16 марта 2880 г. [Giorgini et al., 2002]. К сожалению, на сегодняшний день физические параметры астероида и положение его оси вращения известны недостаточно точно. В зависимости от их значений вероятность столкновения оценивается в диапазоне от 0 до 1/300. Дело в том, что на интервале почти в 880 лет астероид подвергается действию различных сил, в том числе таких, действием которых на менее значительных интервалах времени обычно пренебрегают по причине их малого влияния. К ним, в частности, относится световое давление и эффект Ярковского (см. главы 3 и 7). Последний эффект зависит от положения оси вращения астероида. На интервале в 880 лет эти эффекты становятся вполне ощутимыми для тела диаметром 1,1 км и в состоянии оказать заметное влияние на вероятность столкновения. Неопределенность с положением оси вращения не позволяет дать более точный прогноз. В самом худшем случае, т. е. когда вероятность столкновения составляет 1/300, оценка угрозы столкновения по Палермской шкале равна +0,17. Это означает, что риск столкновения с данным астероидом в 2880 г. превосходит фоновый риск, определяемый возможными случайными столкновениями до 2880 г. с телами той же самой или большей энергии, в 10^0,17 раз, т. е. примерно в полтора раза. На сегодняшний день астероид (29075) 1950 DA — единственное тело, для которого риск столкновения на исследованном интервале времени (для разных тел он различен, но обычно составляет сто лет) превосходит фоновый риск.