Книга: Кеплер. Движение планет. Танцы со звездами.

ЗВЕЗДНАЯ МАССА

Массу Солнца можно вычислить, наблюдая за любой планетой Солнечной системы и зная расстояние от нее до Солнца и период обращения планеты. Так же мы можем рассчитать массу Земли, зная расстояние от Земли до Луны и период обращения нашего спутника, – для этого необходимо всего лишь применить закон Кеплера в интерпретации Ньютона. При помощи этого же принципа и уже указанного закона Кеплера можно рассчитать звездную массу двойных звезд, и это вычисление является практически единственным непосредственным методом вычисления звездной массы. К счастью, частью двойной системы являются многие звезды, так что к настоящему времени наработана обширная статистическая база звездных масс. Масса звезды тесно связана с ее светимостью, или световым потоком, излучаемым в секунду времени. Соотношение массы и светимости имеет следующий вид:

L аМ^х ,

где L – светимость, М – масса, х – показатель степени, равный примерно 3 или чуть больше для звезд с очень большой массой.

Подобное соотношение справедливо не только для звезд, относящихся к звездам главной последовательности, которые состоят из идеального газа, 4Н -› Не.

Двойные звезды могут быть визуальными, спектральными и фотометрическими. В случае визуально-двойных звезд при длительном изучении, например в течение нескольких лет, можно наблюдать, как обе звезды вращаются вокруг общего центра масс, двигаясь при этом по эллиптической орбите. Спектрально-двойные и фотометрические двойные звезды обычно расположены настолько близко, что расчеты крайне затруднительны, так как мы можем наблюдать лишь одну звезду, хотя мы и знаем, что на самом деле их две. В этом случае периоды обращения, как правило, гораздо меньше, и их определение не требует много времени.

Спектрально-двойные звезды можно обнаружить с помощью спектральных наблюдений в течение нескольких ночей. Излучение одного компонента такой звездной системы с определенной периодичностью смещается то в красную, то в синюю часть спектра в зависимости от того, удаляется или приближается звезда. Если спектр второго компонента демонстрирует аналогичные смещения, но в противофазе, то можно утверждать, что перед нами двойная система. Подобное поведение вызвано эффектом Доплера и движением звезды по орбите и позволяет довольно точно определить период ее обращения.

В случае фотометрических двойных звезд мы наблюдаем изменение кривой силы света, то есть отношения светового потока ко времени, из-за того, что звезды затмевают друг друга. Для наблюдения этого явления необходимо, чтобы плоскость орбиты находилась на линии видимости.

Информация, получаемая в ходе наблюдений за двойными системами, меняется в зависимости от типа наблюдения. Расчеты могут быть более или менее сложными, однако принцип остается неизменным. Не будем вдаваться в подробности формул определения массы и обратимся непосредственно к результатам. В случае визуально-двойных звезд мы наблюдаем эллипс обеих и можем рассчитать их массу:

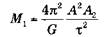
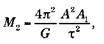
где А₁ – большая полуось звезды 1, А₂ – большая полуось звезды 2, М₁ и М₂ – их массы, А = А₁ + А₂ – расстояние между звездами, ? – период обращения. Эти уравнения выводятся непосредственно из закона Кеплера. Таким образом:

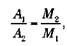
так как центр тяготения должен находиться ближе к более массивной звезде. Если 2 является планетой, М₂ << M₁ таким образом, число А₁ ничтожно мало. Это означает, что А приблизительно равно A₂ , и мы получаем закон Кеплера:

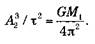
Это крайне важно для ситуаций, когда мы не видим звезды с большей массой, например в случае с черной дырой. Именно с помощью этого метода была вычислена масса черной дыры, находящейся в центре Млечного Пути.

В случае спектрально-двойных звезд можно рассчитать только массы, помноженные на наклон орбиты i, или угол между плоскостью орбиты и лучом зрения.

Если двойные звезды одновременно и спектральны, и фотометричны, могут быть получены особенно обширные данные. Возможно вычислить наклон орбиты, обе массы, а также расстояние между звездами и их радиусы.

Центр Солнца движется относительно центра тяжести Солнечной системы – барицентра. Это движение определяется двумя наиболее массивными планетами – Юпитером и Сатурном – и имеет вид почти круговых движений, согласованных с периодами обращения этих планет (около 12 и 29,5 года). Солнце удаляется от центра масс Солнечной системы на величину, приблизительно равную диаметру Солнца, и вращение происходит вокруг оси, которая, как кажется, расположена на поверхности планеты. Наблюдая за этим движением, можно сделать вывод о существовании Юпитера, хоть он и невидим.

Этот факт очень полезен при обнаружении планет, не относящихся к Солнечной системе. Боковое смещение не несет особой информационной нагрузки, так как его непросто оценить, а вот движение по эллипсу может быть прослежено с помощью эффекта Доплера. Благодаря этим методам исследования были обнаружены многочисленные планетные системы, находящиеся за пределами Солнечной.