Книга: Достучаться до небес: Научный взгляд на устройство Вселенной

МАСШТАБИРОВАНИЕ ЧЕПУХИ

МАСШТАБИРОВАНИЕ ЧЕПУХИ

Научные исследования невозможны без практики, без технической подготовки и упорства. Но этого мало. Аутисты — не говоря уже о некоторых научных сотрудниках и многих чиновниках — нередко демонстрируют прекрасную техническую осведомленность, но им откровенно не хватает творческого подхода и воображения. В наши дни достаточно сходить в кинотеатр, чтобы убедиться, что одного только упорства и технических достижений без воображения и креативности недостаточно. Бесконечные сцены, в которых одни нарисованные чудовища сражаются с другими нарисованными чудовищами, сами по себе, конечно, выглядят внушительно, но такому сюжету, как правило, не хватает энергии, чтобы полностью захватить многих зрителей. По крайней мере я часто засыпаю в кинозале, несмотря на все световые и звуковые эффекты.

Для меня самые захватывающие фильмы — те, что обращаются к серьезным вопросам и реальным идеям, но передают их через простые примеры, которые каждый человек может понять и оценить. Фильм «Касабланка» рассказывает о патриотизме и любви, о войне и верности, но хотя Рик и говорит Ильзе, что «не нужно много ума, чтобы понять: проблемы трех маленьких людей в этом безумном мире ничего не стоят», именно эти трое повинны в том, что фильм меня захватил (плюс, конечно, работа Петера Лорре и Клода Рейнса).

В науке тоже правильные вопросы часто ставит тот, кто удерживает в уме одновременно и глобальное, и частное. Существуют великие проблемы, решить которые мечтает каждый, и существуют маленькие вопросы, которые кажутся несложными. Поставить перед собой крупную проблему, как правило, недостаточно, потому что к реальному продвижению обычно приводит решение небольших вопросов. В одной песчинке действительно можно увидеть целый мир.

Важная способность любого творческого человека—это умение правильно поставить вопрос. Творческие люди стремятся распознать перспективный, интересный и, самое главное, реальный путь к истине и в конце концов верно сформулировать вопросы. В науке лучший подход — это сосредоточенность на небольшой проблеме и при этом учет глобальных вопросов. Иногда крохотная проблема или противоречие становятся ключом к большому открытию.

Революционные идеи Дарвина отчасти выросли из повседневных наблюдений за птицами и растениями. Вычисление прецессии перигелия орбиты Меркурия не было результатом ошибки измерений, а указывало на ограниченность действия законов физики Ньютона. Этот результат стал одним из свидетельств в пользу теории гравитации Эйнштейна. Несовпадения, которые кому?то покажутся слишком мелкими и незначительными, на самом деле могут показать путь к новым концепциям, но лишь тем, кто сумеет взглянуть на проблему под правильным углом.

Эйнштейн поначалу вообще не собирался заниматься гравитацией. Он пытался разобраться в следствиях недавно разработанной теории электромагнетизма. Ученый сосредоточился на странных или даже противоречивых аспектах симметрии, как все тогда думали, пространства и времени, а закончил тем, что революционным образом изменил наше мировоззрение. Эйнштейн считал, что во всем должен быть смысл; ему хватило настойчивости, чтобы догадаться в конце концов, в чем этот смысл может заключаться.

Или взглянем на современные научные исследования. Вопрос о том, почему некоторые взаимодействия не могут происходить согласно суперсимметричным теориям, кому?то может показаться пустяком. В 1980–е гг. моего коллегу Дэвида Каплана засмеяли, когда он попытался в Европе поговорить о подобных проблемах. Но оказалось, что этот вопрос — богатый источник новых данных как о суперсимметрии, так и о ее нарушениях; на его базе возникли новые гипотезы, которые сегодня готовятся проверять экспериментаторы на БАКе.

Я твердо верю в то, что Вселенная непротиворечива и что любое отклонение подразумевает какую?то интересную, но пока не открытую особенность. После того как я заявила об этом на одной презентации, какой?то блогер написал, что я идеалистка. На самом же деле для многих ученых убежденность в непротиворечивости Вселенной — одна из основных, вероятно, движущих сил при выборе тем и вопросов для изучения.

Кроме того, многие известные мне творческие люди обладают способностью удерживать в сознании одновременно значительное число вопросов и идей. Любой может заглянуть в Google и выяснить что?то об интересующем его предмете, но, если вы не умеете компоновать факты и идеи нестандартным образом, вам вряд ли удастся обнаружить что?нибудь новое. Именно при столкновении разнонаправленных идей нередко рождаются новые научные гипотезы и произведения искусства.

Многие предпочитают работать линейно. Но это означает, что на первом же непреодолимом препятствии, при первых же сомнениях в верности выбранного пути путешествие заканчивается. Подобно многим писателям и художникам, ученые продвигаются вперед скачкообразно. Как правило, это нелинейный процесс. Некоторые детали головоломки удается понять, другие приходится временно отодвигать в сторону и оставлять на потом. Мало кому удается до конца разобраться в теории после одного–единственно- го прочтения. Приходится считать, что когда?нибудь мы до конца во всем разберемся, что мы можем себе позволить пока пропустить кое–какие неясности, а потом, добравшись до конца, к ним вернуться. Приходится погружаться в тему с головой, чтобы продолжать работу над ней — и над понятными кусками, и над непонятными.

Известно, что Томас Эдисон однажды заметил: «Гений — это один процент вдохновения и 99 процентов пота». А по словам Луи Пастера, «в области исследований счастье улыбается только натруженному уму». Именно поэтому увлеченные исследователи иногда находят ответ на свои вопросы. Но случается, что ответы эти находятся совсем не там, где предполагалось. Александр Флеминг не искал лекарство от инфекционных болезней. Он просто заметил, что грибок уничтожает колонии бактерий Staphylococci, изучением которых он в то время занимался, и распознал потенциальное терапевтическое значение этого факта, хотя понадобилось еще десять лет и труд множества других людей, прежде чем пенициллин стал мощным лекарством, по–своему изменившим мир.

Нередко при определенной широте базы рассматриваемых вопросов возникают и побочные достижения. Работая над суперсимметрией, мы с Раманом Сандрамом получили в конце концов свернутое дополнительное измерение, позволяющее решить проблему иерархии. Потом мы еще раз внимательно посмотрели на уравнения, перенесли их на более широкий контекст и обнаружили, что бесконечное свернутое пространственное измерение может существовать, не порождая никаких противоречий с известными наблюдаемыми фактами или законами природы. Мы занимались физикой элементарных частиц — совершенно другой темой. Но одновременно мы старались удерживать в сознании и общую картину мира. Мы не забывали про глобальные вопросы о природе пространства даже тогда, когда наше внимание было поглощено частными моментами, такими как иерархия масштабов масс в Стандартной модели.

Важно, что ни Раман, ни я не были специалистами по теории относительности, так что к своим исследованиям мы подошли без всякой предвзятости. Ни нам и никому другому в голову бы не пришло, что теория гравитации Эйнштейна допускает существование невидимого бесконечного измерения, пока уравнения не показали нам, что это возможно. Мы упрямо разбирались в следствиях наших уравнений, не зная, что в кругах ученых, занятых теорией относительности, бесконечное дополнительное измерение считалось невозможным.

Тем не менее мы далеко не сразу щерились в том, что правы. Ни Раман, ни я не собирались слепо хвататься за радикальную идею. Выходить за пределы привычных пространства и времени имело смысл только после того, как мы и многие другие физики убедились, что традиционные идеи здесь не годятся. Хотя дополнительное измерение — достаточно свежая гипотеза, теория относительности Эйнштейна продолжает действовать. Поэтому мы могли воспользоваться готовыми уравнениями и математическим аппаратом, чтобы понять, как поведет себя наша гипотетическая вселенная.

Позже другие использовали результаты этого исследования и приняли модель с дополнительными измерениями за отправной пункт в собственных поисках новых физических идей, которые, возможно, будут применимы в какой?нибудь вселенной без дополнительных измерений. Подойдя к этой проблеме буквально, физики увидели в ней возможности, которых прежде никто не замечал. Такой подход помог ученым выйти за рамки трехмерности.

Всякому, кто вторгается на новые территории, приходится мириться с массой неопределенностей — от них невозможно избавиться, пока проблема не будет решена полностью. Даже если вы начинаете с прочного фундамента существующих знаний, то, изучая новые явления, вы рано или поздно столкнетесь с неизвестностью и неопределенностью, хотя, конечно, рискуете вы при этом куда меньше, чем канатоходец. Не только космонавты, но и ученые, и художники дерзко стремятся «туда, где никто еще не бывал». Но их дерзость не слепа и не случайна, и они не пренебрегают достижениями предшественников, даже если речь идет о совершенно новых идеях и безумных экспериментах, которые, кажется, и реализовать?то невозможно. Исследователи стремятся быть готовыми ко всему. Именно для этого нужны правила, уравнения и представления о непротиворечивости. Это страховка, которая защищает нас во время путешествия по неизвестным землям.

По словам моего коллеги Марка Камионковски, «хорошо быть амбициозным и смотреть в будущее». Но главное все?таки — ставить реалистичные цели. Один студент, достигший больших успехов в изучении бизнес–менеджмента, заметил, что базой недавнего успешного экономического роста, раздувшегося затем в экономический пузырь, в значительной мере была именно креативность. Но, заметил он также, недостаток сдерживающих факторов привел к тому, что пузырь лопнул.

В качестве примера противоречивых намерений, которые внушают человеку уверенность и осторожность, можно привести даже самые важные открытия прошлого. Научный журналист Гэри Таубс однажды сказал мне, что ученые — одновременно самые уверенные и самые неуверенные люди на свете. Именно это противоречие гонит их все время вперед: с одной стороны, каждый из них уверен в том, что движется вперед, а с другой — самым жестким образом проверяет любые свои выводы. Творческий человек должен верить, что он может добиться многого, и при этом постоянно помнить о тех, у которых ничего не получилось.

Выдвигая смелые, подчас даже авантюрные идеи, ученые иногда очень неохотно представляют их миру. Известнейшие ученые Исаак Ньютон и Чарльз Дарвин много лет не решались поделиться с окружающими своими революционными идеями. Исследования Дарвина растянулись на десятилетия, и книга «Происхождение видов» вышла лишь после громадного количества наблюдений. Ньютоновы «Начала» представили теорию всемирного тяготения, на разработку которой у автора ушло больше десяти лет. Ньютон не публиковал трактат, пока не получил достаточных доказательств того, что тела произвольной геометрической формы (не только точечные) тоже притягиваются с силой, обратно пропорциональной квадрату расстояния. Именно в процессе доказательства этого закона Ньютон разработал методы дифференциального и интегрального исчисления.

РИС. 81. Задача: не отрывая карандаша от бумаги, соединить девять точек четырьмя отрезками прямой

Иногда требуется заново сформулировать проблему, чтобы увидеть ее в новом свете и заново определить границы, а затем найти решение там, где на первый взгляд никакого решения и быть не может. Для успеха начатой работы нередко очень важны упорство и вера — не в бога, а в то, что решение все?таки существует. Истинные ученые — и вообще творческие люди — никогда не останавливаются, оказавшись в тупике. Если проблема не решается одним способом, они пробуют решить ее иначе. Если впереди непреодолимое препятствие, они роют тоннель, ищут другое направление или поднимаются в воздух и составляют карту местности. Именно здесь вступает в игру воображение. Чтобы продолжать, мы должны верить в то, что ответ реально существует, а мир изначально логичен, и эту логику мы в конце концов обязательно обнаружим. Посмотрев на проблему под верным углом, можно заметить связи, которые в противном случае обязательно пропустишь.

В качестве иллюстрации можно привести известную задачу, в которой требуется, не отрывая карандаша от бумаги, соединить девять точек четырьмя отрезками прямой (рис. 81). Если держаться в пределах образованного точками квадрата, решения у задачи не существует, но ведь никто не задавал вам такого ограничения! Стоит выйти за пределы квадрата, и решение появляется (рис. 82). В этот момент вам, возможно, придет в голову, что проблему можно переформулировать еще несколькими способами. Если точки будут большими, можно ограничиться тремя линиями. Если сложить бумагу (или воспользоваться очень широким пером, как предложила создателю задачи одна маленькая девочка), хватит и одной линии.

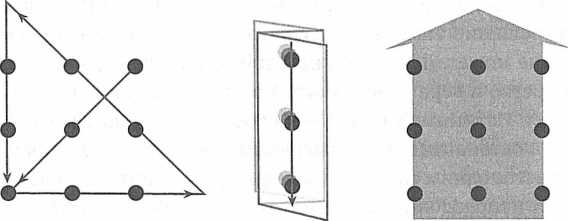
РИС. 82. Возможные креативные решения задачи о девяти точках включают вариант выхода за пределы квадрата, складывание бумаги так, чтобы точки сошлись на одной прямой, и использование широкого пера или грифеля

Эти решения — не обман и не нарушение правил. Правда, они были бы обманом, если бы в задаче имелись дополнительные ограничения. К сожалению, система образования зачастую загоняет мышление в жесткие рамки, когда человек сам отсекает «лишние» возможности. В книге «Кварк и ягуар» (The Quark and the Jaguar) Мюррей Гелл–Манн цитирует «историю про барометр» профессора физики Вашингтонского университета Александра Каландры. Суть истории такова: преподаватель, сомневаясь в оценке, задал студенту вопрос о том, как можно измерить высоту здания при помощи барометра. Студент ответил, что можно привязать барометр к веревке и спустить с крыши на землю, а затем измерить длину веревки. Когда преподаватель возразил, что решение должно быть основано на законах физики, экзаменуемый предложил измерить время падения барометра с крыши или длину тени от барометра и от здания в заданное время дня. Студент предложил также один нефизический способ: пойти к коменданту и предложить ему барометр в обмен на информацию о высоте здания. Возможно, это были не те ответы, которые хотел услышать преподаватель. Но студент верно — и остроумно — подметил, что личные ограничения преподавателя не входят в условия задачи.

Когда в 1990–е гг. я вместе с другими физиками начала думать о дополнительных пространственных измерениях, мы не просто стали мыслить шире, мы буквально вышли за пределы знакомого трехмерного пространства. Мы размышляли о мире, в котором сама сцена, на которой мы решали свои проблемы, неожиданно оказалась больше, чем мы думали. Представив себе такой мир, мы сумели отыскать в нем потенциальные решения проблем, которые годами беспокоили специалистов по физике элементарных частиц.

Надо заметить, что научные достижения возникают не в вакууме. Они всегда опираются на идеи предшественников. Хорошие ученые прислушиваются друг к другу. Иногда для получения верного вопроса или ответа достаточно просто внимательно выслушать, понаблюдать или прочесть чью?то статью. Мы часто сотрудничаем, привлекая в проект ученых разных специальностей; кроме того, это помогает сохранить объективность.

Каждый ученый хочет первым сделать важное открытие; тем не менее мы умеем учиться друг у друга и делиться друг с другом результатами своей работы; умеем мы и работать над одной общей темой. Иногда случайная фраза, сказанная кем?то из коллег, становится ключом к интересной проблеме или решению. У каждого ученого, конечно, бывают свои озарения, но мы часто обмениваемся мыслями, вместе прорабатываем следствия и вносим поправки — или начинаем все сначала, если оказывается, что первоначальная идея не работает. Мы постоянно придумываем новые гипотезы, одни сохраняем про запас, другие отбрасываем.

Это наш хлеб. Именно так мы работаем, именно так продвигаемся вперед. Это не плохо. Это прогресс.

Одна из важнейших задач, которые я выполняю при работе с аспирантами, заключается в том, чтобы внимательно следить, не мелькнет ли в их рассуждениях какая?нибудь свежая перспективная идея, даже если сами они пока не могут как следует ее сформулировать; стоит прислушиваться также к критике моих построений. Возможно, такой взаимный обмен — лучший способ научить творчеству (или, по крайней мере, поддержать его).

Конкуренция тоже играет важную роль в научном процессе — впрочем, как и в большинстве других занятий. При обсуждении креативности художник Джефф Кунс рассказал нам, что в юности его сестра занималась живописью и в какой?то момент он вдруг понял, что способен рисовать лучше. Один молодой продюсер объяснил, что конкуренция стимулирует его и его коллег и заставляет заимствовать у других лучшие идеи и методы, а значит, и развивать собственные. Известный повар Дэвид Чан выразил аналогичную мысль чуть более откровенно. При посещении нового ресторана у него иногда возникает мысль: «Это здорово! Почему я об этом не подумал?»

Ньютон тянул с публикацией до завершения исследований. Но при этом он, вполне вероятно, внимательно следил за своим конкурентом Робертом Гуком, который тоже знал об обратной пропорциональности квадрату расстояния, но математического аппарата для доказательства этого закона у него не было. Тем не менее работа Гука, вероятно, подтолкнула Ньютона к публикации результатов. Дарвин тоже принял окончательное решение о публикации, узнав о том, что над аналогичными эволюционными идеями работает некий Альфред Рассел Уоллес и, если он еще немного потянет с публикацией, слава первооткрывателя достанется конкуренту. И Дарвин, и Ньютон хотели полностью прояснить для себя свои теории, прежде чем публиковать их, и работали над ними до полной уверенности — или по крайней мере пока их не стали догонять конкуренты.

Вселенная то и дело дает нам понять, что она умнее нас. Уравнения или наблюдения подсказывают новые идеи, которые еще недавно никому не приходили в голову и для подтверждения которых в будущем потребуются оригинальные, креативные эксперименты. Без неопровержимых экспериментальных свидетельств ни один ученый не придумал бы квантовую механику; я подозреваю, что точную структуру ДНК и мириады явлений, в сумме образующих жизнь, практически невозможно было бы угадать, если бы мы не столкнулись лицом к лицу с «подсказками».

Научные исследования — органичный процесс. Мы вовсе не обязательно знаем, к чему идем, но эксперименты и теории служат нам на этом пути ценными проводниками. Подготовка и мастерство, сосредоточенность и упорство, умение задавать нужные вопросы и доверять собственному воображению — вот качества, которые помогают нам в поиске истины. Полезны также широта взглядов, общение с коллегами, желание превзойти предшественников или коллег и вера в то, что ответы существуют. Какими бы мотивами ни руководствовались ученые, каких бы навыков не потребовали от них новые теории, исследования будут продолжаться и вглубь вещества, и вовне. Мы будем с нетерпением ждать информации об открытии новых законов жизни, которых еще немало скрыто во Вселенной.