Книга: Наша математическая вселенная

Может ли физическая реальность быть математической?

Может ли физическая реальность быть математической?

Реальность, лишённая времени

Ответить на эти вопросы нам поможет Эйнштейн. Он учил, что существует два эквивалентных способа думать о физической реальности: как о трёхмерном вместилище пространстве, где всё изменяется во времени, и как о четырёхмерном вместилище, называемом пространство-время, которое просто существует — неизменное, никогда не создаваемое и никогда не уничтожаемое.[70] Эти два взгляда соответствуют «лягушачьей» и «птичьей» точкам зрения на реальность (гл. 9). Вторая соответствует взгляду физика, изучающего математическую структуру реальности, подобно тому, как птица рассматривает землю с большой высоты. А первая — это внутренний взгляд наблюдателя, живущего внутри этой структуры, подобно лягушке, живущей на участке, который охватывает взглядом птица.

Математически пространство-время — это пространство с четырьмя измерениями: первые три являются знакомыми нам измерениями пространства, а четвёртое измерение представляет собой время. На рис. 11.1 временное измерение я отложил по вертикали, а пространственные измерения по горизонтальным направлениям. Во избежание недоразумений я нарисовал только два из трёх пространственных измерений, x и y, поскольку при попытке визуализировать четырёхмерные объекты у меня из ушей начинает идти дым… На рисунке показана Луна, движущаяся вокруг Земли по круговой орбите, — ради удобства я изобразил орбиту гораздо меньше, чем она должна быть при соблюдении масштаба, и сделал ещё некоторые упрощения.[71] В правой части рисунка показана «лягушачья» точка зрения: пять снимков пространства с Луной в разных положениях и неизменным положением Земли. В левой части рисунка показана «птичья» точка зрения: то, что лягушке кажется движением, заменено неизменной формой в пространстве-времени. Поскольку Земля не движется, она всё время остаётся на одном месте в пространстве, а потому в пространстве-времени представлена вертикальным цилиндром. Луна выглядит гораздо интереснее и представляется в пространстве-времени спиралью, задающей, где находится небесное тело в разные моменты времени. Рассмотрите обе части рисунка, чтобы уяснить, как они связаны: это важно для нашего разговора. Чтобы получить мгновенный снимок пространства (справа) по пространству-времени (слева), вы делаете горизонтальный срез пространства-времени в тот момент, который вас интересует.

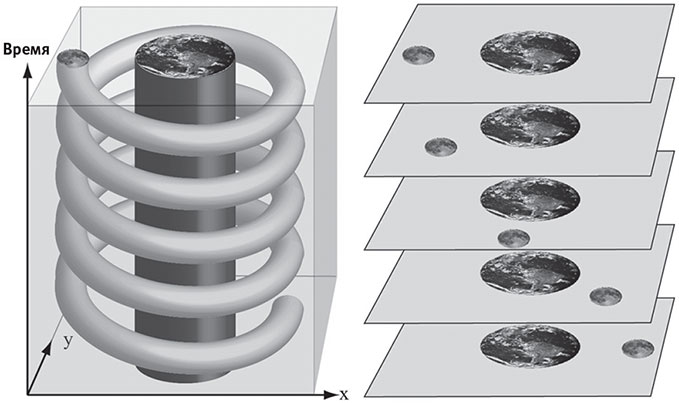
Рис. 11.1. Движение Луны вокруг Земли. Мы в равной мере можем думать о нём как о положении в пространстве, которое изменяется во времени (справа), и как о неизменной спиральной форме в пространстве-времени (слева), соответствующей математической структуре. Снимки пространства (справа) — просто горизонтальные сечения пространства-времени (слева).

Обратите внимание: не пространство-время существует внутри пространства и времени, а, напротив, пространство и время существуют внутри пространства-времени. Я утверждаю, что наша внешняя физическая реальность является математической структурой, то есть по определению абстрактной, неизменной сущностью вне пространства и времени. Как мы увидим, эта математическая структура соответствует «птичьей», а не «лягушачьей» точке зрения на нашу реальность, так что она должна содержать пространство-время, а не только пространство. Эта математическая структура содержит также дополнительные элементы, соответствующие материи в нашем пространстве-времени. Однако это не меняет её вневременного характера: если бы история Вселенной была шахматной партией, математическая структура соответствовала бы не одной позиции, а всей игре (рис. 10.6). Если бы история Вселенной была кинофильмом, она соответствовала бы не отдельному кадру, а целому DVD. Так что с «птичьей» точки зрения траектории объектов, движущихся в четырёхмерном пространстве-времени, напоминают клубок спагетти. Там, где лягушка видит нечто, движущееся с постоянной скоростью, птица наблюдает прямую, ещё не сваренную макаронину. Там, где лягушка видит Луну, обращающуюся вокруг Земли, птица видит спиральку-ротини (рис. 11.1). Там, где лягушка видит сотни миллиардов звёзд, движущихся вокруг Галактики, птица видит сотни миллиардов переплетающихся макаронин. Для лягушки реальность описывается ньютоновскими законами движения и гравитации. Для птицы реальность — это геометрия макарон.

Прошлое, настоящее и будущее

«Извините, сколько сейчас времени?» — думаю, вы тоже задаёте этот вопрос, как если бы на фундаментальном уровне существовала такая вещь, как сейчас. При этом вы, наверное, никогда не обращались к прохожему с вопросом: «Извините, сколько сейчас места?» Если вы действительно безнадёжно заблудились, то, вероятно, спросите что-нибудь вроде: «Извините, а где я?» — подтверждая тем самым, что вы интересуетесь не свойством пространства, а, скорее, своим собственным свойством: положением в пространстве в момент, когда задан вопрос. А когда вы спрашиваете о времени, то в действительности интересуетесь не свойством времени, а, скорее, собственным положением во времени. Пространство-время содержит все места и все времена, поэтому нет никакого сейчас, как нет и здесь. Так что в научном (но не в бытовом) отношении корректнее спросить: «Когда я?» Пространство-время подобно карте космической истории без отметки «Вы находитесь здесь». Если вам для ориентировки нужна такая отметка, я рекомендую пользоваться телефоном с часами и GPS-приёмником.

Когда Эйнштейн писал, что различие между прошлым, настоящим и будущим — не более чем иллюзия, хотя и весьма навязчивая, он имел в виду, что эти понятия не имеют объективного смысла в пространстве-времени. На рис. 11.2 показано, что когда мы упоминаем о настоящем, то подразумеваем временное сечение пространства-времени, соответствующее моменту, когда мы об этом подумали. Мы называем будущим и прошлым части пространства-времени, расположенные выше и ниже этого сечения. Это аналогично тому, как вы пользуетесь словами «здесь», «передо мной» и «позади меня», чтобы указывать на разные части пространства относительно своего текущего положения. Часть, находящаяся перед вами, очевидно, не менее реальна, чем часть позади вас: в самом деле, если вы идёте вперёд, часть того, что сейчас находится перед вами, в будущем окажется позади вас, а сейчас оно находится позади многих других людей. Аналогично в пространстве-времени будущее столь же реально, как и прошлое — части пространства-времени, которые сейчас находятся в вашем будущем, окажутся в вашем прошлом. Поскольку пространство-время статично и неизменно, никакая его часть не может изменить статус своей реалистичности, так что все его части должны быть одинаково реальными.[72]

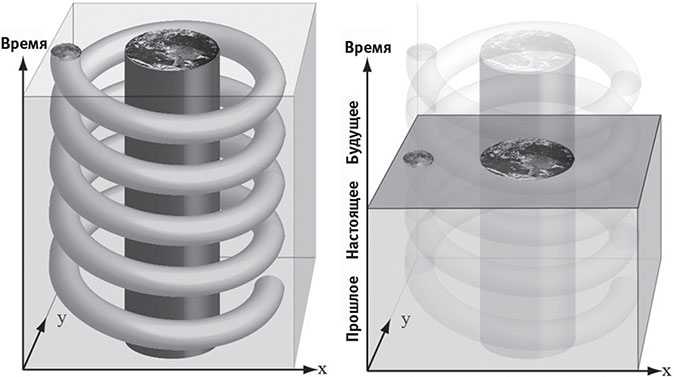
Рис. 11.2. Различие между прошлым, настоящим и будущим существует только с «лягушачьей» точки зрения (справа), но не с «птичьей», с которой воспринимается математическая структура (слева) — в последнем случае вы не можете спрашивать, который час, а только — в каком вы времени.

Итак, время — не иллюзия, однако течение времени иллюзорно. То же самое касается изменений. В пространстве-времени существует будущее, да и прошлое не исчезает. Когда мы объединяем эйнштейновское классическое пространство-время с квантовой механикой, мы получаем квантовые параллельные вселенные (гл. 8). Это означает, что существует много прошлых и будущих, и все они реальны, что не отменяет неизменную математическую природу полной физической реальности.

Так мне всё это видится. Однако, хотя данное представление о неизменной реальности проверено временем и восходит к самому Эйнштейну, оно остаётся спорным и порождает оживлённую научную дискуссию. Например, Брайан Грин в книге «Скрытая реальность» выражает тревогу из-за утраты фундаментального статуса таких понятий, как изменение и созидание: «Я предпочитаю думать, что существуют процессы, пусть даже гипотетические… которые, как нам представляется, приводят к возникновению этой мультивселенной».[73] Ли Смолин в книге «Возвращение времени» идёт ещё дальше и показывает, что не только изменения реальны, но время вообще может быть единственной реальной вещью. На противоположном краю спектра стоит Джулиан Барбур, обосновывающий в книге «Конец времени» не только иллюзорность изменений, но и возможность описывать реальность вообще без введения понятия времени.

Могут ли быть математическими пространство-время и «материя»?

Итак, пространство-время может рассматриваться как математическая структура. Но что можно сказать о материи, находящейся в пространстве-времени, скажем о книге, которую вы сейчас читаете? Как всё это может быть частью математической структуры?

В последние годы мы видели, что разнообразные вещи, которые казались совершено не связанными с математикой, например тексты, звуки, изображения, фильмы, представляются математически с помощью компьютеров и передаются по интернету в виде наборов чисел. Присмотримся поближе к тому, как компьютеры это делают: природа делает нечто очень похожее, чтобы представить всё окружающее нас вещество.

Я только что набрал на клавиатуре английское слово word, и лэптоп представил его в памяти последовательностью из четырёх чисел: 119 111 114 100. Каждую строчную букву он передаёт числом, равным 96 плюс порядковый номер буквы в алфавите (a = 97, w = 119 и т. д.). Одновременно мой компьютер играл композицию De Profundis Арво Пярта, которая тоже представляется последовательностью чисел. Эти числа интерпретируются не как буквы, а как положения, которые должны занимать мембраны аудиоколонок в каждое из 44 100 различных мгновений каждой секунды, что, в свою очередь, вызывает колебания воздуха, которые мои уши и мозг интерпретируют как звук. Когда я нажал клавишу w, лэптоп воспроизвёл на дисплее изображение w, также представленное числами. Хотя изображения на дисплее кажутся гладкими и непрерывными, в действительности он состоит из 1920 ? 1200 пикселов, расположенных в виде прямоугольной сетки (рис. 11.3), и цвет каждого пиксела представляется тремя числами в диапазоне от 0 до 255 каждое, задающими интенсивность идущего от пикселя красного, зелёного и голубого света. Подходящее сочетание этих трёх цветов позволяет воспроизвести все интенсивности всех цветов радуги. Прошлым вечером, когда мы с сыновьями смотрели видео с Youtube, лэптоп делил на пикселы не только два пространственных измерения дисплея, но и временное измерение, разбивая его на 30 кадров в секунду.

Физики часто моделируют в трехмерии некоторые явления вроде урагана, вспышки сверхновой или образования планетной системы. Для этого мы делим трёхмерное пространство на трёхмерные пикселы (вокселы). Мы также делим четырёхмерное пространство-время на четырёхмерные вокселы. Каждый четырёхмерный воксел представляет, что происходит в соответствующем месте и времени с помощью группы чисел, кодирующих всё, что имеет отношение к делу, скажем, температуру, давление, плотности и скорости различных веществ в вокселе. Например, при моделировании Солнечной системы воксел, соответствующий центру Солнца, будет содержать чрезвычайно большое число, выражающее температуру, а воксел за пределами Солнца, содержащий почти пустое пространство, будет иметь близкое к нулю число, выражающее давление. Числа в соседних вокселах удовлетворяют некоторым соотношениям, которые описываются математическими уравнениями, а когда компьютер выполняет моделирование, он, подобно игроку в судоку, пользуется этими соотношениями, чтобы определять отсутствующие числа. Если компьютер готовит прогноз погоды, то пространственно-временные вокселы, соответствующие настоящему моменту, заполняются измеренными значениями давления воздуха, температуры воздуха и т. д. Компьютер затем применяет соответствующие уравнения для вычисления значений, которые записываются в пространственно-временные вокселы, соответствующие завтрашнему дню и остальным дням недели.

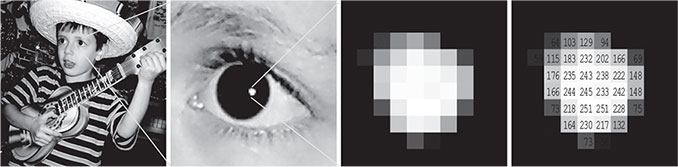
Рис. 11.3. Компьютеры обычно представляют полутоновые изображения, храня число для каждой точки (пиксела) фотографии (самая правая картинка). Чем больше число, тем выше интенсивность света от данного пиксела: 0 представляет чёрный цвет (нет никакого света), а 255 — белый цвет. Подобным же образом так называемые поля в классической физике представляются в каждой точке пространства-времени числом, которое, грубо говоря, задаёт количество «материи», присутствующей в каждой точке.

Подобные симуляции, математически отображающие некоторые аспекты внешней физической реальности, делают это приближённо. Пространство-время, конечно, не состоит из грубых вокселов, которые применяются для моделирования погоды, и это одна из причин, по которой метеорологические прогнозы часто неточны. И всё же мысль, что с каждой точкой пространства-времени связана группа чисел, весьма глубока, и, я думаю, она кое-что говорит нам не только о нашем описании реальности, но и о самой реальности. Одно из фундаментальных понятий современной физики, поле, устроено именно так: это нечто, представимое числами в каждой точке пространства-времени. Например, существует поле температур, соответствующее воздуху вокруг нас: в каждой точке имеется строго определённая температура, не зависящая от любых изобретённых человеком вокселов, и её значение можно измерить с помощью термометра (или пальца, если не требуется высокой точности). Существует также поле давления: в каждой точке есть число, выражающее давление — его можно измерить барометром или своими ушами, которые начинают болеть, если это число сильно отклоняется от нормы, а также воспринимают звук, если давление колеблется во времени.

Сейчас известно, что ни то, ни другое поле не является истинно фундаментальным: они, по сути, показывают, как быстро в среднем движутся молекулы воздуха, и их числа перестают быть чётко определёнными, если попытаться измерить их в субатомных масштабах. Однако существуют другие поля, которые кажутся фундаментальными, образующими часть ткани нашей внешней физической реальности. Магнитное поле определяется не одним (как температура), а тремя числами в каждой точке пространства-времени, задающими его величину и направление. Вы, вероятно, измеряли магнитное поле с помощью компаса, наблюдая, как его стрелка устанавливается вдоль магнитного поля Земли, направленного к северу. Стрелка выравнивается быстрее, если магнитное поле сильнее — например вблизи магнитно-резонансного томографа. Другой пример — электрическое поле, которое также представляется тремя числами, задающими его величину и направление. Простой способ измерить его — по силе, с которой оно действует на заряженный объект, например, когда ваши волосы электрически притягиваются к пластмассовой расчёске. Электрическое и магнитное поля можно элегантно объединить в электромагнитное поле (представляется шестью числами в каждой точке пространства-времени). Свет — это волны, бегущие по электромагнитному полю (гл. 7), и если наш физический мир — это математическая структура, то весь свет во Вселенной (который кажется нам физическим) связан с шестью числами в каждой точке пространства-времени (чисто математической сущностью). Эти числа подчиняются математическим соотношениям — уравнениям Максвелла (рис. 10.4).

Следует сделать оговорку: то, что я сейчас описал, соответствует пониманию электричества, магнетизма и света в классической физике. Квантовая механика усложняет картину (но не делает её менее математической), заменяя классический электромагнетизм квантовой теорией поля — основанием всей современной физики элементарных частиц. В квантовой теории поля волновая функция задаёт степень, в которой является реальной любая возможная конфигурация электрического и магнитного полей. Волновая функция сама по себе математический объект, абстрактная точка в гильбертовом пространстве.

Квантовая теория поля утверждает (гл. 7), что свет состоит из частиц, называемых фотонами. Грубо говоря, числа, составляющие электрическое и магнитное поля, могут рассматриваться как информирующие о числе фотонов в каждый момент в каждом месте. Так же, как есть электромагнитное поле, напряжённость которого соответствует числу фотонов в каждый момент в каждом месте, существуют и другие поля, соответствующие прочим известным элементарным частицам. Например, напряжённость электронного поля и напряжённость кваркового поля связаны с числом электронов и кварков в каждый момент времени в каждом месте. В классической физике все движения всех частиц в пространстве-времени соответствуют набору чисел в каждой точке четырёхмерного математического пространства — математической структуре. В квантовой теории поля волновая функция задаёт степень, в которой является реальной любая возможная конфигурация каждого из этих полей.

Физики ещё не нашли математическую структуру, которая описывала бы все аспекты реальности, включая гравитацию (гл. 7). Но пока нет признаков того, чтобы теория струн или другой кандидат на роль такого описания был бы менее математическим, чем квантовая теория поля.

Описание или эквивалентность?

Прежде чем идти дальше, необходимо разобраться с важным семантическим моментом. Большинство моих коллег-физиков скажет, что внешняя физическая реальность (по крайней мере приближённо) описывается математикой. Я же утверждаю, что внешняя физическая реальность является математикой, точнее, математической структурой.

Всё, о чём до сих пор шла речь в этой главе, предполагает, что нашу внешнюю физическую реальность можно описать математической структурой. Если в учебнике физики появится долгожданная «теория всего» (ТВ), её уравнения будут полностью описывать математическую структуру, которая является внешней физической реальностью. Я использую здесь слово «является», а не «соответствует», поскольку, если две структуры эквивалентны, то (как подчёркивал израильский профессор Мариус Коэн)[74] не существует осмысленного контекста, в котором они не являются одним и тем же. Вспомните мощное математическое понятие эквивалентности из гл. 10, которое охватывает самую суть математических структур: если два полных описания эквивалентны, то они описывают одну и ту же вещь.[75] Это означает, что если некие математические уравнения описывают и нашу внешнюю физическую реальность, и математическую структуру, то наша внешняя физическая реальность и эта математическая структура есть одно и то же. И тогда верна гипотеза математической Вселенной: наша физическая реальность является математической структурой.

Вспомните, что две математические структуры эквивалентны, если можно попарно связать их сущности так, чтобы сохранялись все отношения. Если вы можете таким образом спарить каждую сущность нашей внешней физической реальности с соответствующей сущностью в математической структуре (например, «данное значение напряжённости электрического поля в данной точке физического пространства соответствует данному числу в математический структуре»), то наша внешняя физическая реальность соответствует определению того, что значит быть математической структурой. Фактически она и есть эта математическая структура.

В гл. 10 мы видели, что если хочется избежать принятия гипотезы математической Вселенной, то можно отбросить гипотезу внешней реальности, утверждающую, что существует внешняя физическая реальность, полностью независимая от людей. Можно затем утверждать, что Вселенная почему-либо оказалась состоящей из материи, идеально описываемой математической структурой, но она имеет и другие свойства, которые этой структурой не описываются и вообще не могут быть описаны абстрактным, свободным от «багажа», независимым от человека способом. Однако, думаю, эта точка зрения заставила бы перевернуться в гробу Карла Поппера (гл. 6), который подчёркивал: научные теории должны иметь наблюдаемые проявления. В то же время, поскольку математическое описание по нашему допущению является идеальным, отвечающим за всё, что может наблюдаться, все дополнительные украшения, которые могли бы сделать нашу Вселенную нематематической, по определению не имели бы наблюдательных проявлений и поэтому были бы совершенно ненаучны.