Книга: Наша математическая вселенная

Мультиверс объединённый

Мультиверс объединённый

Я никак не мог выкинуть из головы мысль: не представляют ли мультиверсы I и III уровней в некотором смысле одно и то же? Можно ли их каким-либо образом объединить, подобно тому, как Максвелл объединил электричество и магнетизм в электромагнетизм, а Эйнштейн объединил пространство и время в пространство-время? С одной стороны, кажется, что их природа различна. Параллельные вселенные I уровня (гл. 6) находятся где-то очень далеко в нашем старом добром трёхмерном пространстве, а параллельные вселенные III уровня из этой главы могут располагаться прямо здесь, в смысле наших трёх измерений, но они отделены от нас в гильбертовом пространстве (абстрактном пространстве с бесконечным числом измерений, в котором обитает волновая функция). С другой стороны, мультиверсы I и III уровней имеют много общего. Жауме Гаррига и Александр Виленкин показали, что параллельные вселенные I уровня, порождённые космологической инфляцией, содержат те же последовательности событий, что и эвереттовские квантовые параллельные вселенные. (Я пришёл к тем же выводам.) Если квантовое событие вызывает два события, происходящих в квантовой суперпозиции (рис. 8.10), фактически расщепляя ваше будущее на две параллельные квантовые ветви, то параллельный квантовый исход, о котором вы сейчас ничего не знаете, происходит также и здесь, в вашей квантовой ветви, но очень далеко в пространстве.

И был ещё один источник беспокойства: Энтони Агирре. Он один из моих лучших друзей, и наши жизни во многом параллельны: мы оба пытаемся найти баланс между карьерой и двумя маленькими сыновьями, оба захвачены глобальными проблемами, вместе основали Институт фундаментальных вопросов (fqxi.org), филантропически финансируемую организацию, которая вкладывается в высокорисковые, но обещающие большую отдачу физические исследования, непривлекательные для обычных фондов. Чем же Энтони меня беспокоил? «Что если одни параллельные вселенные равнее других?» — спрашивал он.

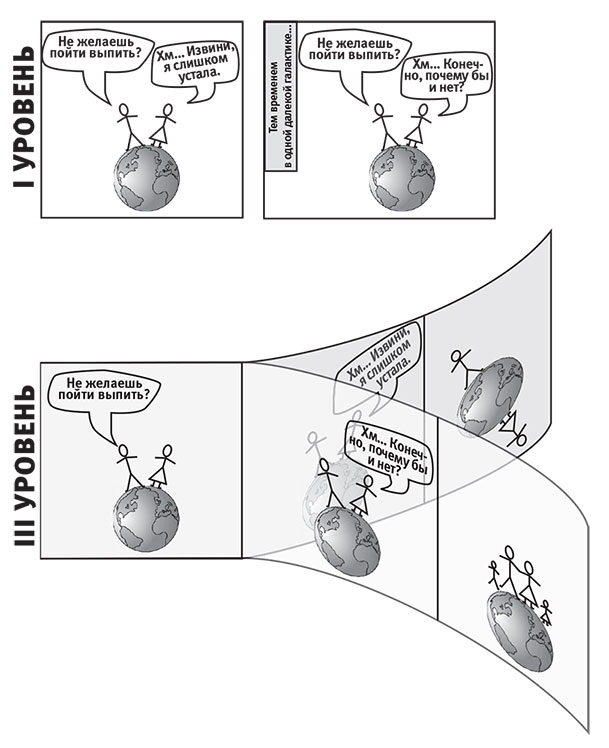
Рис. 8.10. Сравнение параллельных вселенных уровней I и III. В то время как параллельные вселенные I уровня находятся очень далеко в пространстве, вселенные, относящиеся к III уровню, располагаются прямо здесь, возникая за счёт квантовых событий, которые расщепляют классическую реальность на расходящиеся истории. Тем не менее III уровень не добавляет новых историй к имеющимся на уровнях I или II.

Энтони обращал внимание на то, что объяснение квантовых вероятностей, которое я дал в этой главе, отлично подходит, если исходы имеют одинаковую вероятность (как в случае квантовых карт, которые падают лицом вверх или вниз с равными шансами в 50 %), но всё усложняется, если вероятности неодинаковы. Предположим, например, что в начале эксперимента вы чуть наклонили карту, и вероятность (квадрат волновой функции) падения лицом вверх составляет теперь 2/3, а лицом вниз — 1/3. Тогда рис. 8.2 выглядел бы по-прежнему — на нём осталось бы 2 ? 2 ? 2 ? 2 = 16 исходов после четырёх попыток, а наиболее вероятным исходом стало бы падение карты лицом вверх в 50 %, а не в 2/3 случаев. Эверетт спасает положение и всё же умудряется предсказать вероятность 2/3, опираясь на то утверждение, что некоторые исходы имеют большую меру существования, нежели другие (причём её можно вычислить как квадрат волновой функции). Это работает, и многие учёные пытались выстроить тщательно продуманную аргументацию, почему именно квадрат волновой функции должен играть эту роль. Однако Энтони убедил меня в том, что это страшный недостаток в остальном элегантных эвереттовских построений. Меня часто спрашивают, верю ли я в реальность параллельных вселенных Эверетта. Ответ «Да, но… хм… как бы сказать… Некоторые из них реальнее, чем другие» звучит крайне неубедительно.

В марте 2008 года Энтони рассказал мне о возможном подходе к решению этой проблемы (я вскоре его изложу), предложенном его гарвардским профессором Дэвидом Лэйзером. Мы провели два замечательных часа в кафе «Белмонт», исписывая салфетки математическими символами, — но всё впустую. Мы не смогли заставить работать эту математику. Но я не мог и выкинуть эту идею из головы. Два года спустя я нашёл статью, написанную в 1968 году теоретиком квантовой гравитации Джимом Хартлом, которая, как я чувствовал, содержала ещё одну деталь пазла. Но, сидя поздним вечером 6 марта 2010 года в своей квартире в Уинчестере, я никак не мог сложить части головоломки. Я решил прогуляться. К моему удивлению, всего через пять минут на холоде у меня в голове наконец-то щёлкнуло! Я вдруг понял, как разом решить обе проблемы: объединить два уровня мультиверсов и объяснить неравные вероятности. Это не давало мне уснуть до трёх часов ночи и поглотило весь следующий день, который я провёл в изумительном, подобном трансу состоянии, которое испытываешь, когда совершенно что-либо понимаешь. Я чувствовал, что это одна из самых замечательных догадок, посетивших меня с момента переоткрытия декогеренции девятью годами ранее, и я не мог остановиться, пока не написал четырёхстраничный набросок статьи для Энтони.

Рис. 8.11 иллюстрирует ключевую идею. Допустим, вы собираетесь выполнить эксперимент с квантовыми картами, слегка наклонив карту, так что ожидаете увидеть её упавшей лицом вверх и выиграть 100 долларов с вероятностью 2/3. В традиционном виде (слева в каждом прямоугольнике на рис. 8.11) вначале имеется одна ваша копия, а затем, после эксперимента, — одна либо две копии, в зависимости от того, коллапсирует волновая функция или нет. Если верна копенгагенская интерпретация, то будет существовать один определённый исход, полученный случайным образом. Если же прав Эверетт, то будет две параллельных вселенных, и каждая содержит по одному вашему экземпляру: одна, в которой вы радуетесь выигрышу, другая — где вы опечалены проигрышем.

Пусть теперь существует мультиверс I уровня (гл. 6), как и предполагает современная космология. Это означает, что бесконечное число неотличимых от вас копий выполняет точно тот же эксперимент на других планетах очень-очень далеко (на рисунке это показано рядом нейтральных смайликов). В своих подсчётах я предположил, что уравнение Шрёдингера для волновой функции описывает всю совокупность частиц, составляющих все ваши копии и копии эксперимента.

Что в итоге? Если волновая функция коллапсирует, получится один случайный исход для всего бесконечного пространства (мультиверса I уровня), так что вы окажетесь довольным на 2/3 планет и опечаленным на 1/3 — здесь нет ничего удивительного. Если же Эверетт прав в том, что коллапса не происходит, то результатом станет целое бесконечное пространство в квантовой суперпозиции различных состояний, в каждом из которых вы радуетесь на одних планетах и печалитесь на других. А теперь — самое интересное. Все эти состояния пространства оказываются неотличимы друг от друга: вы счастливы ровно на 2/3 бесконечного множества планет! Любая конечная последовательность планет со счастливыми и несчастливыми исходами в одном из этих состояний обнаружится где-то в ином месте пространства в каждом из остальных состояний. Можно подумать, что должны существовать отличающиеся состояния пространства, скажем, такое, где вы счастливы на всех до единой планетах. Однако, опираясь на уравнение Шрёдингера и математические свойства гильбертова пространства, я смог доказать, что получаемая в итоге волновая функция равна простой суперпозиции бесконечного числа неотличимых состояний. Нас с Энтони по ряду причин это поразило.

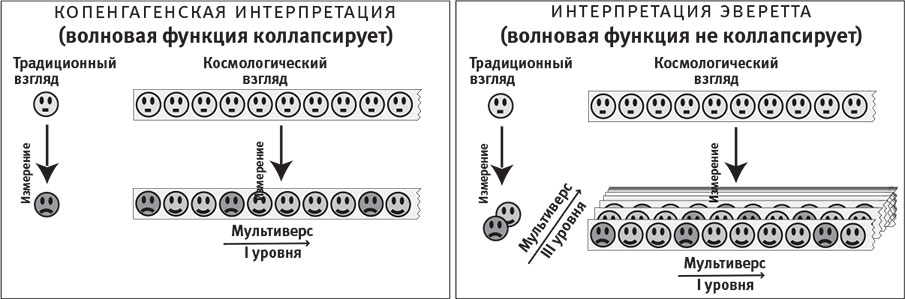
Рис. 8.11. Как объединяются мультиверсы I и III уровней? Каждый кружок — это планета, где вы ставите деньги на то, что квантовая карта упадёт лицом вверх. Вначале вы в нейтральном настроении, а после измерения радуетесь выигрышу либо опечалены проигрышем. Карта чуть-чуть наклонена, так что вы ожидаете выиграть с вероятностью 2/3. Эти планеты обычно очень удалены друг от друга, скажем, на гуголплекс метров в разных направлениях, однако я нарисовал их в ряд, чтобы проиллюстрировать идею.

Прежде всего, великая дискуссия о том, коллапсирует ли волновая функция, завершилась великим разочарованием: это попросту не имеет значения. На рис. 8.11 показано, что независимо от того, прав Эверетт или нет, вы будете счастливы на 2/3 планет. На самом деле, обе стороны спора о коллапсе вышли из него изрядно помятыми. В копенгагенской интерпретации спорная концепция коллапса вводится, чтобы избавиться от досадных параллельных вселенных и добиться единственности исхода события, но, как видно из рисунка, это уже не помогает: даже при наличии коллапса получаются параллельные вселенные с обоими исходами. Для интерпретации Эверетта отличительным признаком служили параллельные вселенные III уровня (квантовые), но на рисунке видно, что их можно спокойно игнорировать, поскольку все они неразличимы. В этом смысле мультиверсы уровней I и III объединяются: если имеется бесконечное пространство с мультиверсом I уровня, то можно игнорировать связанные с ним параллельные вселенные III уровня, поскольку на практике все они представляют собой лишь идентичные копии. Не исключено, что III уровень можно объединить и со вторым, но пока мы не смогли это доказать.

Во-вторых, рис. 8.11 демонстрирует происхождение неравных вероятностей, перенося множественные миры Эверетта в наше старое доброе трёхмерное пространство. Различные исходы случаются не только где-то в труднопредставимом математическом гильбертовом пространстве, но и где-то очень далеко в нашем собственном пространстве, которое мы исследуем с помощью телескопов. Суть в том, что после того, как карта упала, но до того момента, когда вы открыли глаза, у вас нет способа узнать, какой из множества копий самого себя вы являетесь, поскольку до этого последнего момента все они чувствуют себя субъективно неразличимыми. Поскольку вы знаете, что 2/3 ваших копий, открывая глаза, видят карту лежащей лицом вверх, вам кажется, что вы случайным образом обнаружите её в этом положении с вероятностью 2/3. Это аналогично тому способу, каким представители французской знати первоначально ввели понятие вероятности для оптимизации своей стратегии в азартных играх. Если в игре вам известно лишь то, что вы окажетесь в одной из множества равновероятных ситуаций (соответствующих, скажем, тому, как перетасована сдаваемая колода), то вы можете считать, что вероятность вашего выигрыша — это просто доля тех ситуаций, в которых вы выигрываете, среди всех возможных.

В-третьих, это позволяет нам предложить космологическую интерпретацию квантовой механики. В ней мы интерпретируем волновую функцию объекта не как описание некоего странного воображаемого ансамбля возможностей для данного объекта, а как реальную пространственную совокупность идентичных копий объекта, существующих в бесконечном пространстве. Более того, испытываемая вами квантовая неопределённость просто отражает вашу неспособность определить своё положение в мультиверсе I уровня, то есть узнать, какая из бесконечного числа ваших копий, разбросанных по космосу, обеспечивает ваше субъективное восприятие.

В некоторых областях соавторы статей по традиции перечисляют свои имена в алфавитном порядке. В космологии, однако, мы обычно делаем так, чтобы порядок авторов отражал величину их вклада в статью. В большинстве случаев очевидно, кто проделал наибольшую работу, но в данном случае определить это было трудно. К тому моменту, когда мы были готовы представить статью для публикации, и Энтони, и я очень серьёзно потрудились и внесли практически равнозначный вклад. У нас состоялся забавный телефонный разговор на эту тему, в котором мы превозносили вклад друг друга и настаивали на том, чтобы поставить имя другого первым. В конце концов я предложил решение, которые понравилось нам обоим: пусть порядок авторов выберет квантовый генератор случайных чисел. В данной вселенной Энтони стал первым автором (http://arxiv.org/pdf/1008.1066.pdf), но если наша статья верна, то я первый автор не только в половине параллельных вселенных III уровня, где применялась данная процедура, но и в половине параллельных вселенных I уровня.

В 2010 году Александр Виленкин пригласил меня сделать доклад по этой статье в Университете им. Тафтса. В аудитории, как и 13 лет назад, сидел Алан Гут. Я вспомнил клюющего носом Алана и приготовился к неизбежному, поскольку не помнил ни одного выступления, на котором он не уснул бы. Однако случилось чудо, и Алан бодрствовал на протяжении всего доклада. Я вижу в этом наивысшее одобрение, которое наша статья могла получить, и кульминацию моей научной карьеры.