Книга: Прикладные аспекты аварийных выбросов в атмосферу

3.10. Высота стабилизации вещества выброса

3.10. Высота стабилизации вещества выброса

Потеря выбросом динамической индивидуальности на фоне турбулентных движений атмосферы не означает, что его вещество полностью идентично веществу окружающей среды. После достижения выбросом максимальной высоты подъема Z_g выброс начинает «растаскиваться» турбулентными вихрями атмосферного воздуха. Его форма уже не может быть моделирована простым геометрическим телом типа сферы или эллипсоида. Вещество выброса подвержено воздействию турбулентных движений атмосферы и стабилизирующему воздействию температурного градиента, возвращающему его к компактной конфигурации.

Естественно, что в этих условиях возникший объем не может рассматриваться как единое динамическое целое — он занимает слишком большие пространственные размеры и имеет поверхность сложной флуктуирующей формы. Для анализа дальнейшего всплытия его вещества, температура которого отлична от Т_?, естественно рассматривать динамику отдельных молей или квазиклубов его вещества, на которые он распался.

Аналогичным образом происходят процессы теплопереноса на участке затухания динамической активности струй. Если атмосферные условия устойчивые, то струйный поток, потерявший свою динамическую индивидуальность при завершении подъема, имеет температурную (и концентрационную) неоднородность и способен продолжать восходящее движение.

Отметим, что подобные температурные (концентрационные) неоднородности продолжают свое поступательное движение в ветровом потоке, являясь фактически динамически пассивными. Рассмотрим оба этих случая.

Стабилизаиия вещества разрушившегося клуба

Назовем фрагменты разрушившегося выброса термоклубами или термооблаками (сокращенно — облаками). В дальнейшем будут использованы оба этих названия.

На завершающем участке подъема подобного выброса изменением кинетической энергии можно пренебречь по сравнению с изменением его внутренней энергии. При этом справедливо уравнение баланса этой характеристики, как для выброса в целом, так и для отдельных его термоклубов.

Внутренняя энергия термоклуба при его подъеме с высоты Z₁ до высоты Z₂ может измениться только за счет охлаждения вовлеченным воздухом. Для моментов времени t_t и t₂ (соответствующих высотам Z_t и Z₂) можно записать следующее соотношение:

(M?)₂=(M?)₁₊M_e·?_? (3.83)

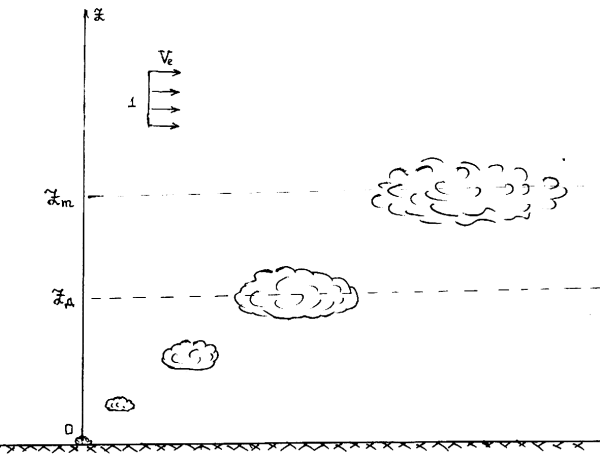
Рис. 3.19. Схема эволюции кратковременного выброса в ветровом потоке: 0 — место инцидента; 1 — ветер; Z_g — высота потери выбросом динамической индивидуальности; Z_m — высота стабилизации вещества выброса.

В этом соотношении:

? = h + gZ; '?_?=h_?+gZ;

где h = С_р — Т — статическая энтальпия единицы массы облака; М,М_е — масса облака и масса вовлеченного в него воздуха; h_? = С_р Т_? — статическая энтальпия ед. массы окружающего воздуха.

Разделим обе части (3.83) на ?Z при учете вида h и считая С_р ? С_р?:

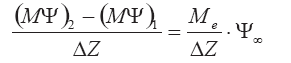
В дифференциальной форме это уравнение записывается так:

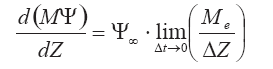
Используя соотношение для вовлечения

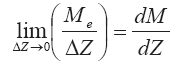
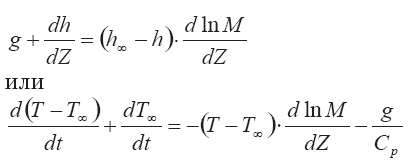
Обозначим дефект температуры клуба

Т — Т_?= ?

и перейдем к высотной координате, используя соотношения

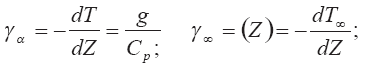
Получаем:

Постоянная С находится из условия: при Z=Z_g u=u_g при задании конкретных значений ?_? (Z) и M(Z), являющихся сложными функциями высоты Z.

Вводя как в работе [132] удельную скорость вовлечения

представляющую собой массу вовлекаемого воздуха, отнесенную к единице высоты Z, получаем для М следующие выражение:

М = е^?Z

Рассмотрим вначале случай постоянных значений ? и ?_?.

Подставив это выражение для массы облака в формулу (3.84) при ?_? = const и ? = const, получаем:

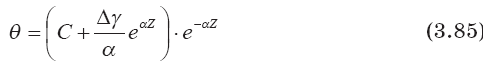
Находим постоянную интегрирования:

при Z=Z_g ? = ?_g

откуда

И окончательное выражение для дефекта температуры термоклуба получаем при подстановке постоянной С в уравнение (3.85):

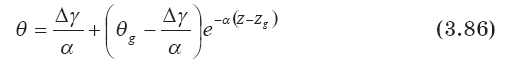
Эта формула при Z_g = 0 совпадает с формулой работы [132], полученной в предложении сохранения потенциальной температуры воздушной частицы при ее адиабатическом смещение вдоль оси Z и при задании исходного уровня Z=0 и начального перегрева ?₀ =Т₀ — Т_?.

Высота стабилизации вещества облака из соотношения (3.86), определяемая из условия 0=0, находится при подстановке вместо Z его предельного значения Z_m.

Поучаем

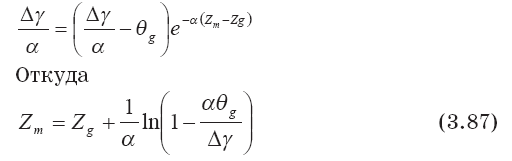
Это выражение является обобщением формулы Л. Махты для высоты стабилизации выброса в атмосфере, которое учитывает процесс неадиабатического расплывания выброса, начинающийся с уровня Z_g — высоты потери его динамической индивидуальности.

Формула Л. Махты [127]:

где ?₀ — разность потенциальных температур на исходном уровне Z = О, дает аналогичные значения для Z_m.

Формула (3.87) имеет смысл при ?у < О, т. е. при устойчивом состоянии атмосферы, когда температура воздуха уменьшается с высотой медленнее, чем на 1 градус на каждые 100 метров.

При этом

На графиках Рис. 3.20 представлено сравнение результатов расчетов высот подъема взрывных выбросов Z_m в зависимости от начального перегрева вещества клуба, выполненное по различным формулам. Отметим, что формула (3.87) при Z = 0 и ?_g0 =Т₀-Т_? дает значения высот подъема взрывных клубов такие же, как по формуле Л. Махты.

Расчеты выполнялись для следующих условий[132]: ? =5 ? 0^-4 1/м (вовлечение 1 кг воздуха на каждые 4 кг облачного воздуха при подъеме его на 500 м) при вариации коэффициента ?_?.

Как следует из графиков этого рисунка, формула Сэттона дает заниженные значения для Z_m при любых начальных перегревах вещества выброса. Этот факт отмечается и в работе [132], где кроме этого подчеркивается качественное согласие результатов расчетов по формуле Махты с экспериментальными данными по высотам стабилизации облаков ядерных взрывов. Расчеты по формуле (3.87) показывают очень сильную зависимость Z_m от степени устойчивости атмосферного воздуха, что является физически правдоподобным.

Для получения выражения для высоты стабилизации выбросов в реальной атмосфере [152] следует исходить из наличия турбулентных пульсаций температуры атмосферного воздуха 

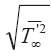
Будем исходить из уравнения (3.83а) при учете связи вовлечения Е в произвольный объем с его боковой поверхностью S_? и изменением массы облака по времени

где удельное вовлечение Е для нагретого вещества выброса, поднимающегося со скоростью W в атмосфере записывается так:

S_? — площадь поверхности термоклуба через которую происходит вовлечение окружающего воздуха; ? — коэффициент вовлечения.

Не ограничивая общности рассуждений, можно считается термоклуб сферическим.

Тогда

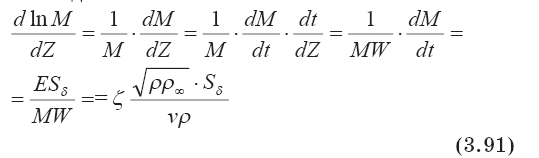
где ? — объем термоклуба

При получении этого выражения была использована связь:

Подставляя вместо S_? и их значения в формулу (3.91), получаем:

При получении этого выражения было использовано условие изоабатичности течения. Коэффициент n учитывает соотношение боковой поверхности и его объема. Если R — радиус эквивалентной сферы, имеющей объем нагретого облака, то n = 3.

Уравнение для определения дефекта температуры термоклуба на высотном уровне стабилизации его вещества запишется в окончательной форме:

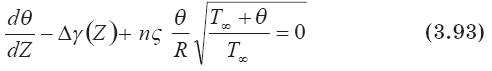
Это уравнение может быть решено численно. Для получения приближенного его решения воспользуемся условием малости ?:

Тогда уравнение (3.93) приобретает приближенный вид:

Его решение записывается так:

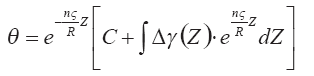
Постоянная С определяется из начального условия для дефекта температуры на уровне потери клубом динамической индивидуальности: при Z = Z_g ? = ?_g

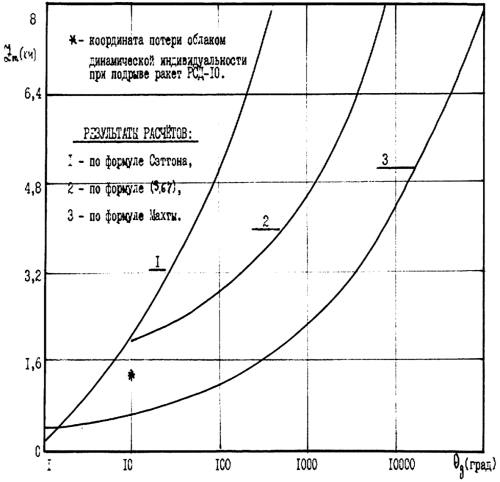
Рис. 3.20. Высота подъема облака взрыва в зависимости от начального перегрева ?_g=T₀ — Т_?.

Откуда получаем

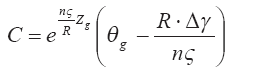
Окончательно для перегрева вещества распавшегося выброса получаем выражение:

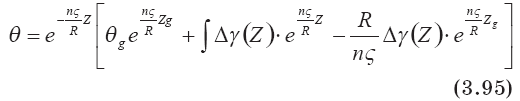
Подставляя вместо ?_?(Z) конкретные значения профиля градиента атмосферной температуры как функции высоты Z, можно получить связь перегрева вещества выброса с его геометрической высотой и с высотой потери им динамической индивидуальности. В частности высота стабилизации вещества клуба в турбулентной атмосфере найдется из соотношения (3.95) при задании на этом высотном уровне значения дефекта температуры вещества клуба в виде: при Z = Z_m ? = ?_m, где

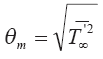
Особенно простой вид имеет выражение для перегрева вещества распавшегося клуба как функции высоты при постоянном значении градиента атмосферного воздуха. Из (3.72) получаем:

Формула (3.96) совпадает с формулой (3.85) при связи коэффициентов вовлечения ?, удельной скорости вовлечения ? и коэффициента формы n в виде следующего соотношения

Отметим, что соотношение (3.96) может быть получено при использовании формулы (3.86) и определений ? и Е.

На уровне стабилизации вещества клуба из (3.96) получаем связь указанных параметров в виде:

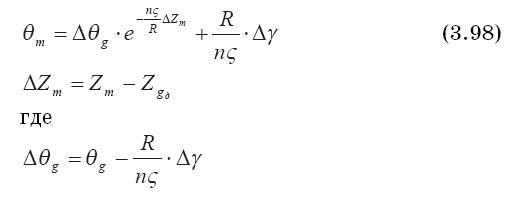
Приращение высотной координаты вещества распавшегося клуба для этого случая может быть определено из уравнения (3.98).

Оно записывается так:

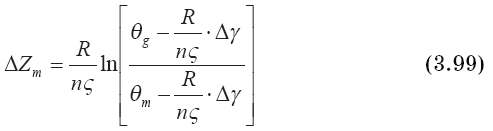
Отметим, что эквивалентный радиус R распадающегося клуба в уравнении (3.93) и производных этого уравнения (соотношения (3.94) — (3.99)) является параметром. В частности, из соотношения (3.99) следует, что чем больше размер рассматриваемого клуба, тем выше он поднимается после разрушения выброса. После потери выбросом динамической индивидуальности на фоне турбулентных движений атмосферы он разрушается, разносится атмосферными пульсациями на отдельные клочья и клубы меньших масштабов. Размеры этих образований — от минимальных, определяемых диссипацией энергии в тепло, до максимальных, соизмеримых с размерами выброса [152].

Для получения наибольших дефектов температуры ?_m и наибольших высот подъема вещества разрушившегося кратковременного выброса Z_m в соотношениях (3.98) и (3.99) вместо R следует брать эффективный радиус выброса при координате его разрушения R = R_g

В качестве иллюстрации полученных выше формул на графиках Рис. 3.21 приводятся результаты расчетов ?Z_m для разных характеристик выбросов и атмосферного воздуха.

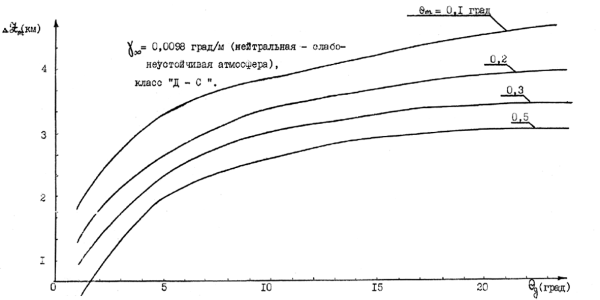
Рис. 3.21. Зависимость величины всплытия вещества разрушившегося взрывного выброса от его перегрева.

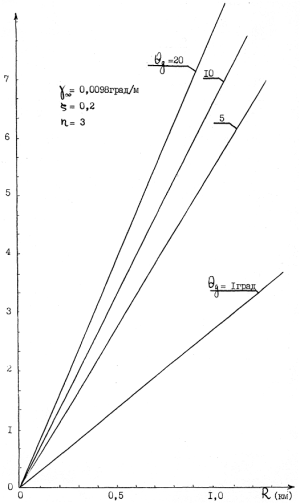
Рис. 3.22. Зависимость всплытия вещества разрушившегося взрыв ного клуба от его радиуса для различных начальных перегревов.

Для получения наибольших дефектов температуры ?_m и наибольших высот подъема вещества разрушившегося кратковременного выброса Z_m в соотношениях (3.98) и (3.99) вместо R следует брать эффективный радиус выброса при координате его разрушения R = R_g

В качестве иллюстрации полученных выше формул на графиках Рис. 3.21 приводятся результаты расчетов ?Z_m для разных характеристик выбросов и атмосферного воздуха.

Графики Рис. 3.22 иллюстрируют зависимость всплытия ?Z_m разрушившихся клубов от их размеров на уровне Z_g для сухобезразличной стратификации (у_? = у_?). Из этих графиков видно, что приращение высотной координаты всплытия вещества клуба линейно зависит от его размера. Чем выше перегрев клуба на уровне Z_q тем больше приращение ?Z_m. Для условий расчета [? = 0,2; n = 3] приращение высотной координаты для клубов реальных размеров при подрывах ТТР (R ? 0,5 ?1 км) при перегревах ?_q ? 2 ?3 град может составить несколько километров.

На графиках Рис. 3.23 показана зависимость высоты теплового всплытия вещества разрушившегося клуба от коэффициента формы для различных степеней турбулентности атмосферного воздуха, характеризующегося коэффициентом ?.

Расчеты проводились при следующих значениях параметров:

R=500 м; ?_g= 5 град; ?_m =0; у_? =2-10^-4 град/м.

Из этого рисунка следует, что чем сильнее раздроблен или «расплющен» выброс после потери им динамической индивидуальности, тем на меньшую высоту поднимается его вещество под действием сил всплытия. Увеличение коэффициента вовлечения д, как и следовало ожидать, приводит к уменьшению величины ?Z_m.

На графиках рис. 3.24 — 3.26 приводятся расчеты приращений высот всплытия вещества взрывного выброса при Z > Z_g для различных состояний атмосферы.

Связь классов устойчивости атмосферного воздуха с вертикальным градиентом температуры у_? в слое 0-200 м и скоростью ветра на уровне флюгера [22,139], приведенные в таблице № 3.7, могут быть распространены на большие высоты. Эти данные использовались нами при сопоставлении класса устойчивости слоя Z > Z_g и вертикального градиента температуры атмосферного воздуха в этом слое.

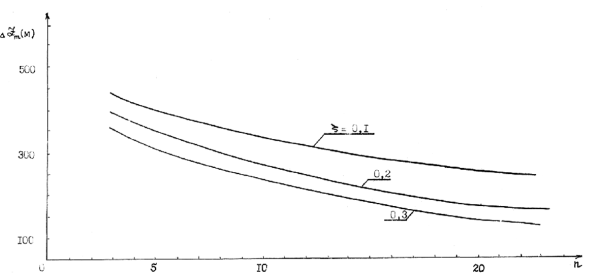
Рис. 3.23. Зависимость теплового всплытия вещества кратковременного разрушившегося выброса от коэффициента формы для различных коэффициентов вовлечения.

Рис. 3.24. Зависимость величины всплытия вещества разрушившегося клуба от его перегрева на высоте Z_g.

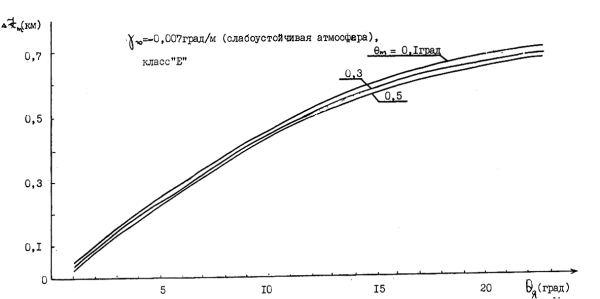
Рис. 3.25. Зависимость величины всплытия вещества разрушившегося клуба от его перегрева на высоте Z_g.

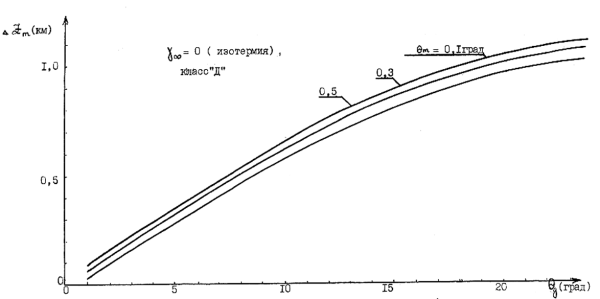
Рис. 3.26. Зависимость величины всплытия вещества разрушившегося взрывного клуба от его перегрева на высоте Z_g.

Таблица № 3.7

Определение классов устойчивости атмосферы по вертикальному градиенту температуры в слое 2-300 м и скорости ветра на уровне флюгера (система классов Пасквилла — Фогта)

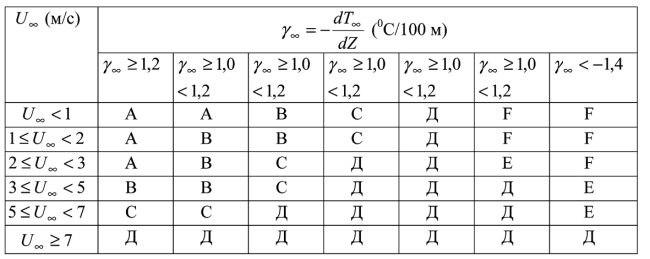
Расчеты проводились при п=3, ? =0,2, R=500 м.

Как следует из графиков Рис. 3.24 — 3.26, где представлены изменения значений ?Z_m в зависимости от перегрева ?_g для различных ?_m, высоты подъема ?Z_m монотонно возрастают при увеличении у_? (при уменьшении устойчивости атмосферы). Наименьший подъем наблюдается для слабоустойчивой (класс Е) и умеренноустойчивой атмосферы (класс F). Для этих классов ?Z_m <0,8 км при рассматриваемых исходных данных для характеристик выброса и атмосферы.

В случае изотермии (у_?=0)всплытие вещества выброса не превосходит километра для диапазона ?_g = 1 ? 20 град. В случае нейтральной атмосферы ?Z_m резко увеличивается, достигая 4 и более километров. Причем, чем меньше среднеквадратичные значения пульсаций температуры атмосферного воздуха, там выше всплытие вещества разрушившегося выброса.

Для умереннонеустойчивой (класс В) атмосферы вещество разрушившегося выброса может быть остановлено стратифицированной атмосферой только при уровне флуктуаций температуры воздуха ?_m, превышающих 1 градус, что весьма маловероятно. При сильно неустойчивой атмосфере (класс А) расчеты по формуле (3.99) становятся не корректными для любых реальных значений параметров атмосферного воздуха. Физически это означает безграничный подъем вещества разрушившегося клуба.

Стабилизация вещества затихающей струи

Рассмотрим теперь закономерности подъема вещества струи после потери ею динамической индивидуальности на фоне турбулентных движений атмосферного воздуха. Такая ситуация гипотетически допускается для сильно устойчивой атмосферы.

Как и в случае с подъемом выброса будем исходить из уравнения сохранения потока внутренней энергии в поперечном сечении струи. Для сечений, отстоящих на малом расстоянии ?l = l₂ — l₁ друг от друга справедливо равенство

где М — расход вещества струи; ? — полная энергия единицы массы газа; h — статическая энтальпия единицы массы газа струи.

Индексы «2», «1» и «?» относятся к сечениям «2», «1» струи и к характеристикам вовлекаемого в струю воздуха.

Деля обе части (3.100) на ?l и устремляя ?l к нулю, приходим к дифференциальному уравнению:

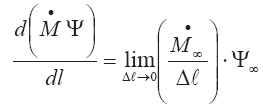
Раскрывая дифференциал в левой части этого соотношения и используя уравнение для вовлечения

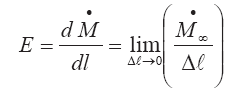
приходим к уравнению относительно дефекта температуры струи ? — Т -Т_? в следующей форме:

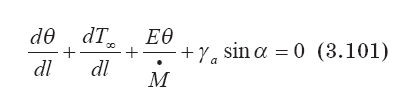
Это уравнение получено при следующем физически обоснованном допушении. На завершающем участке движения струи теплоемкость ее вещества практически не отличается от теплоемкости атмосферного воздуха, а кинетической энергией контрольного газового объема допустимо пренебречь по сравнению с потенциальной и внутренней энергиями.

Для струйного потока

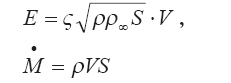
где V — скорость газа струи;

S — площадь поперечного сечения струи;

? — коэффициент вовлечения.

Тогда для изобарического струйного потока:

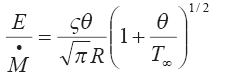
и уравнение (3.101) принимает окончательный вид:

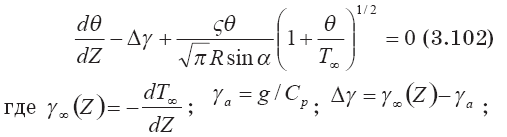
R,? — параметры, определяющие радиус струи и угол наклона рассматриваемого поперечного сечения.

При координате разрушения струйного течения Z = Z_g параметры R и ? имеют значения R_g и ?_g.

При этом уравнение для определения дефекта температуры вещества струи при ее всплытии после потери динамической индивидуальности приобретает следующий вид:

Это уравнение может быть решено численно. Для получения аналитическского приближенного решения, воспользуемся условием малости ? и условием изобаричности течения. Тогда уравнение (3.103) запишется так:

Введем безразмерные параметры:

Тогда

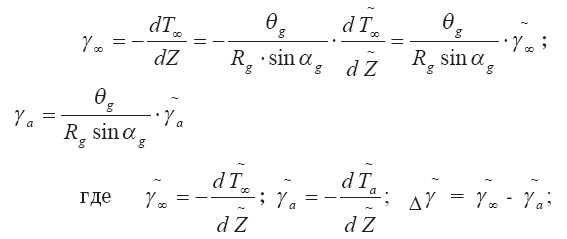
Уравнение (3.104) в безразмерном виде выглядит так:

Его решение

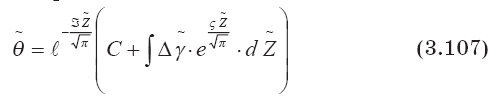
Постоянная С определяется из начального условия: при Z = 1 ? = 1

Высота стабилизации вещества струи в турбулентной атмосфере Z_m может быть найдена из уравнения (3.107) при подстановке в него вместо ? значения

При постоянном распределении температуры с высотой ?_? = const получаем:

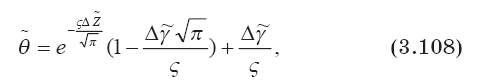
На уровне стабилизации вещества струи уравнение (3.108) приобретает следующий вид:

где ?Z_m = Z_m -1 — безразмерное значение приращения высотной координаты подъема вещества струи.

Из соотношения (3.109) можно найти ?Z_m:

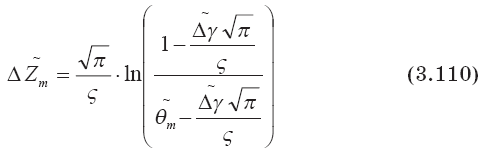
Рис. 3.27. Зависимость приращения высоты выброса при его всплытии после потери им динамической индивидуальности в зависимости от перегрева на этом уровне для различных состояний атмосферного воздуха.

Из формулы (3.110) следует, что тепловой подъем вещества разрушившейся струи тем больше, чем меньше флуктуации температуры атмосферного воздуха, его турбулентность и градиент T_?.

Необходимо отметить, что полученные выше соотношения по подъему и стабилизации вещества струи пригодны, очевидно, лишь для слабовозмущенной атмосферы. Подъем вещества струйного выброса в интенсивно турбулизованной атмосфере на завершающем участке стабилизации его вещества полностью аналогичен подъему кратковременного изолированного выброса. Это объясняется одинаковым механизмом «растаскивания» вещества выбросов на отдельные тепловые облака на участке потери выбросами динамической индивидуальности. Наличие сильно пульсирующего сносящего ветрового потока приводит к распаду струи на отдельные пространственные образования (термоклубы), размеры которых соизмеримы с поперечными размерами струи при Z = Z_g. Дальнейший подъем термоклуба и его стабилизация описываются формулами предыдущего раздела.