Книга: Суперобъекты. Звезды размером с город
Как сейчас отвечают на главный вопрос?
| <<< Назад Вопросы о массе и масса вопросов |
Вперед >>> V. Свойства двойных звезд |
Как сейчас отвечают на главный вопрос?
Пока мы все ждем регистрации гравитационно-волнового сигнала от слияния нейтронных звезд, основной подход к определению условий в недрах компактных объектов таков. У теоретиков есть множество моделей для описания внутреннего строения компактных объектов. Обычно говорят об уравнении состояния: оно связывает плотность вещества с давлением. В рамках любой такой модели можно рассчитать связь массы и радиуса объекта. Теперь задача сводится к одновременному и, возможно, более точному определению масс и радиусов нейтронных звезд.
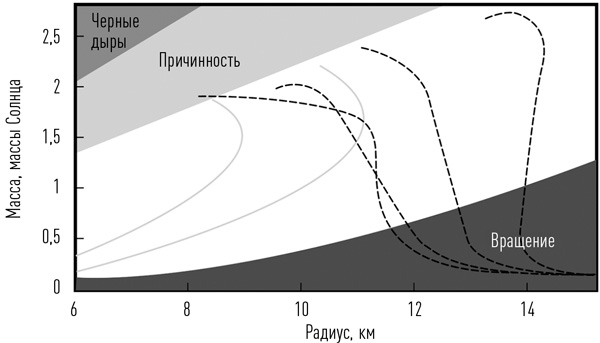
Диаграмма «Масса – радиус» для компактных объектов. По горизонтальной оси отложен радиус, измеряемый по экватору объекта. По вертикальной оси – гравитационная масса. Кривые соответствуют разным теоретическим моделям строения компактных объектов.
В идеале необходимо очень точно определить массу и радиус хотя бы для нескольких нейтронных звезд. Тогда можно надеяться, что все теоретические модели, кроме одной, будут отброшены. В реальности – это очень непростая задача: чаще всего точные измерения масс и радиусов делаются разными способами в разных источниках, поэтому для каких-то звезд есть точные определения масс, а для каких-то – радиусов. Подробнее мы обсудим эти измерения ниже.
Измерения масс и радиусов, а также теоретические кривые наносят на диаграмму «Масса – радиус». Именно здесь разыгрывается драма поиска ответа на главный вопрос физики нейтронных звезд.
На диаграмме «Масса – радиус» сразу выделяется несколько областей. Во-первых, посмотрим на левый верхний угол. Самый уголок отрезается черными дырами: линия соответствует радиусу Шварцшильда. Напомним, что он прямо пропорционален массе объекта и для солнечной массы составляет примерно 3 километра. Однако сразу за черными дырами не начинается территория нейтронных звезд. Отрезается еще кусочек. Не вдаваясь в детали, можно сказать, что часть диаграммы запрещена для реальных объектов, потому что там скорость звука оказывалась бы больше скорости света. То есть если мы как-то искусственно «слепим» такой шарик, то он должен быстро сколлапсировать в черную дыру. Наконец (при бо?льших радиусах и меньших массах) на диаграмме «Масса – радиус» начинается область нейтронных звезд.
Теперь посмотрим на правый нижний угол. Здесь мы можем отрезать кусочек диаграммы для самых быстро вращающихся пульсаров. Чтобы вещество не начало стекать с экватора, надо, чтобы скорость вращения там была меньше первой космической. Значит, для каждой массы и периода вращения есть предельный радиус: если звезда будет больше, то начнется истекание. Линию рисуют для самого быстровращающегося объекта. На сегодняшний день это пульсар PSR J1748-2446ad. Его период составляет примерно 1,4 миллисекунды. За секунду он делает 716 оборотов вокруг своей оси. То есть на экваторе скорость вращения заведомо превосходит 50 000 км/с!
Все остальное разрешено, и диаграмма заполнена теоретическими кривыми. Сразу видно, что они делятся на две основные группы: «нормальные» нейтронные звезды и кварковые звезды.
Кварковые звезды устойчивы благодаря сильному ядерному взаимодействию. Они могут быть очень маленькими, и пока они не слишком выросли, их масса примерно пропорциональна объему. То есть при увеличении массы звезда становится больше.
Для обычных нейтронных звезд это не так. При увеличении массы вещество в их недрах сжимается, поэтому радиус падает. Так же, кстати, ведут себя и белые карлики. В зависимости от уравнения состояния объекты по-разному откликаются на рост массы. Какие-то сжимаются очень существенно, какие-то меняют радиус незначительно. Про первых говорят, что у них «мягкое уравнение состояния», а про вторых – что «жесткое». На диаграмме «Масса – радиус» легко увидеть такое поведение теоретических кривых.
В некоторых случаях при росте массы уравнение вдруг становится из жесткого мягким. Это означает, что в недрах звезды плотность превзошла какое-то критическое значение и произошел фазовый переход: одни частицы превратились в другие. Например, у звезды могло появиться кварковое ядро. Такие объекты называют гибридными.
Сделаем важное уточнение относительно масс и радиусов на диаграмме: поскольку нейтронные звезды – объекты экзотические, то и с их основными параметрами не все так просто. Начнем с массы.
Для каждого обычного объекта (скажем, звезды) можно дать два таких определения массы. Во-первых, мы можем взять полное число барионов (протонов и нейтронов) в этом объекте и умножить его на массу одной частицы (для простоты считаем, что протон и нейтрон имеют равные массы, а массой электронов можно пренебречь). Такую массу называют барионной. Во-вторых, мы можем посмотреть, как наш объект участвует в гравитационном взаимодействии и определить его «гравитационный заряд» – гравитационную массу. Для звезд, планет и других объектов «нормальной» плотности эти две массы обычно с высокой точностью равны. Для нейтронных звезд ситуация иная.
Представьте теперь, что вы взяли железное звездное ядро с массой 1,4 массы Солнца и целиком превратили его в нейтронную звезду без выброса вещества. Какова масса нейтронной звезды? Вовсе не 1,4 солнечной, если мы говорим о гравитационной массе, а меньше процентов на 10–15. А именно эта масса важна практически во всех астрофизических проявлениях объекта (поэтому именно ее наносят на диаграмму). Дело в том, что как масса ядра атома гелия меньше массы четырех протонов за счет энергии связи, так и масса сколлапсировавшего звездного ядра будет меньше исходной. Излишек энергии будет излучен (в основном с помощью нейтрино) в соответствии с E = mc2. То есть при образовании нейтронной звезды барионная масса коллапсирующего ядра не изменилась (считаем, что ни один барион не пропал), а гравитационная резко уменьшилась (за время, необходимое нейтрино, чтобы покинуть горячую протонейтронную звезду).
Теперь о радиусе. Для нейтронной звезды их можно определить несколько, и связано это с эффектами Общей теории относительности. Во-первых, можно измерить расстояние от центра до поверхности. Во-вторых, можно обойти ее по экватору с рулеткой и разделить полученную длину на 2?. В-третьих, можно посмотреть на нее издалека, увидеть диск и определить его радиус. Все эти три значения будут разными. На диаграмме обычно откладывают второе.
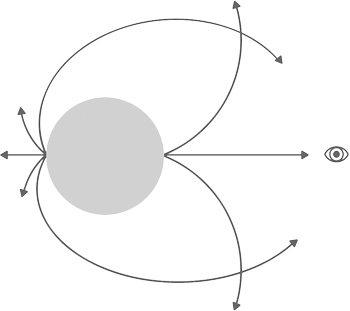
Схематическое изображения искривления световых лучей, приходящих к нам от нейтронной звезды. Свет, вышедший перпендикулярно поверхности, будет удаляться по прямой. А вот световые лучи, испущенные под углом – будут двигаться по искривленным траекториям. Из-за большой концентрации массы пространство искажено, поэтому лучи могут приходить к нам и с обратной стороны. Чем массивнее нейтронная звезда – тем сильнее эффект.
Нейтронная звезда – компактный массивный объект. Внутри него пространство – время устроено по законам Общей теории относительности. Двигаясь из центра наружу, мы попадаем в области с все меньшей и меньшей гравитацией. Меняется метрика пространства, это приводит к последствиям, которые необходимо учитывать при определении длин, в частности – радиуса от центра к поверхности. Он не будет равен тому, который дают измерения только на поверхности.
Свет, приходящий к нам с поверхности нейтронной звезды, тоже двигается по искривленному самой звездой пространству. В частности, из-за этого искривления мы можем видеть часть обратной стороны компактного объекта. Поэтому размеры, наблюдаемые удаленным наблюдателем, будут больше, чем те, что получены измерениями прямо на поверхности.
Астрономы пытаются выжать максимум из доступных на сегодняшний день данных по определению масс и радиусов, чтобы сделать какие-то выводы об уравнении состояния. Кое-что удается сделать, но этого пока явно недостаточно. Сейчас разработаны специальные наблюдательные программы, в том числе с помощью орбитальных обсерваторий, чтобы продвинуться в решении главного вопроса физики нейтронных звезд и поставить точку на диаграмме «Масса – радиус». Видимо, это удастся сделать, изучая двойные системы с нейтронными звездами.
| <<< Назад Вопросы о массе и масса вопросов |
Вперед >>> V. Свойства двойных звезд |
